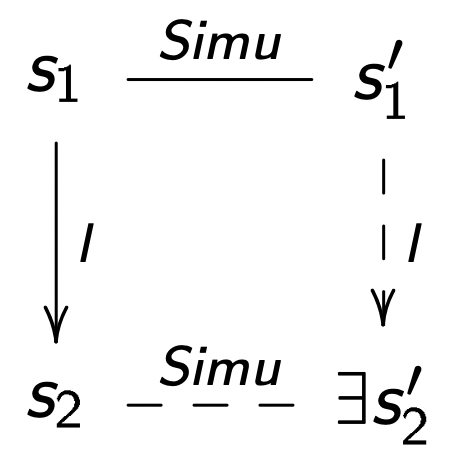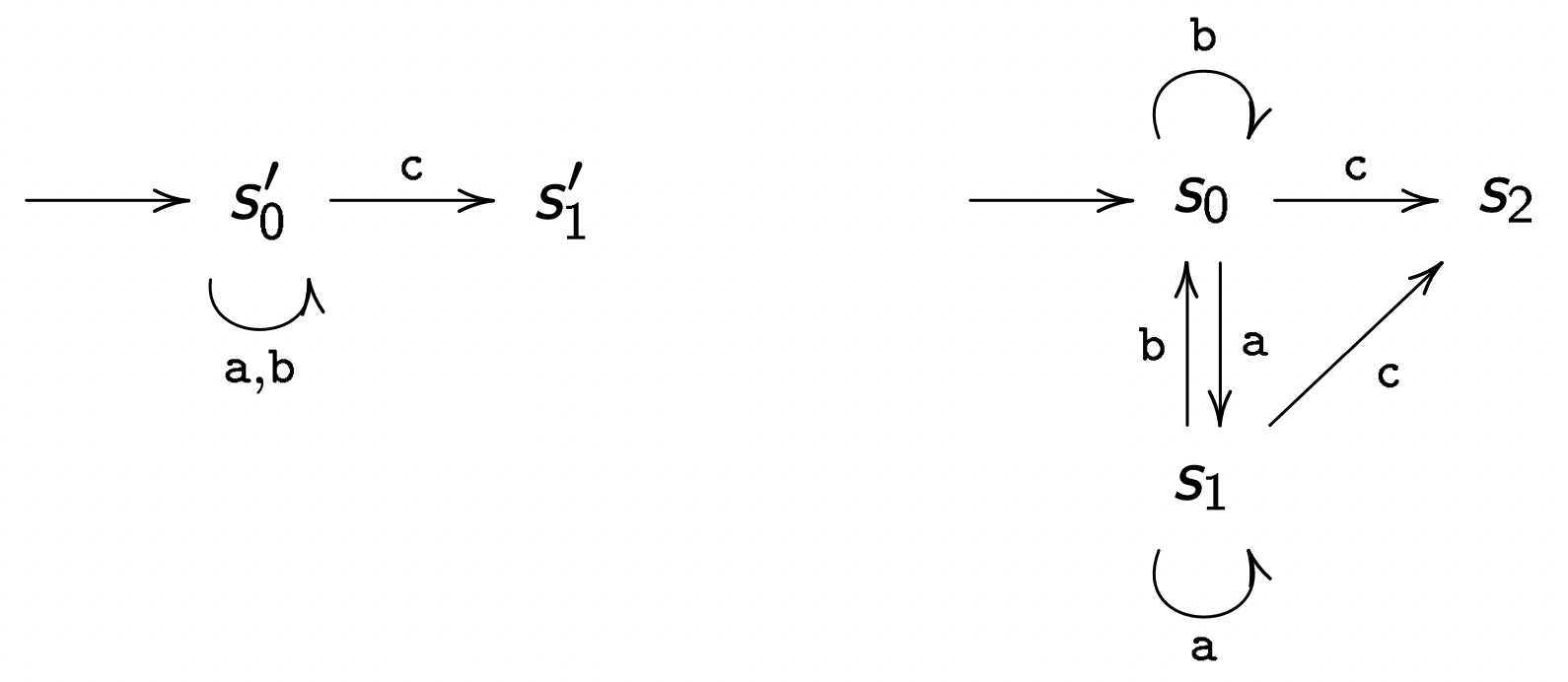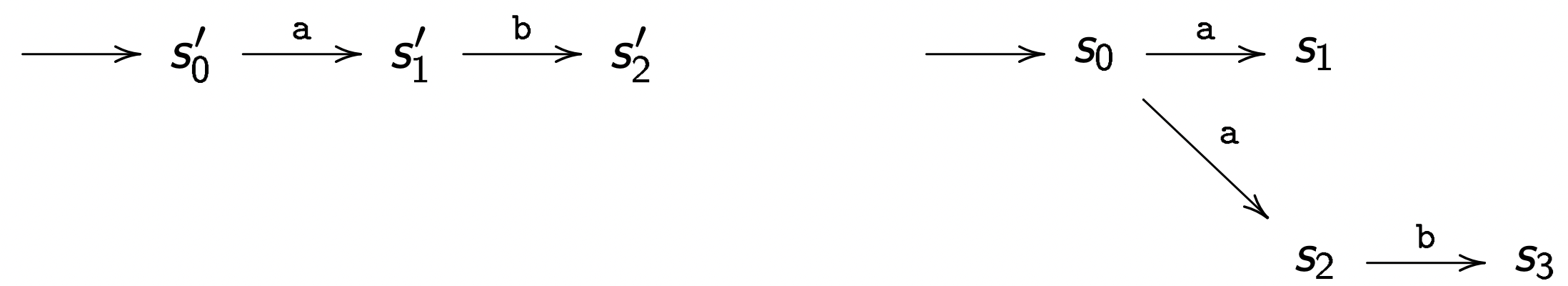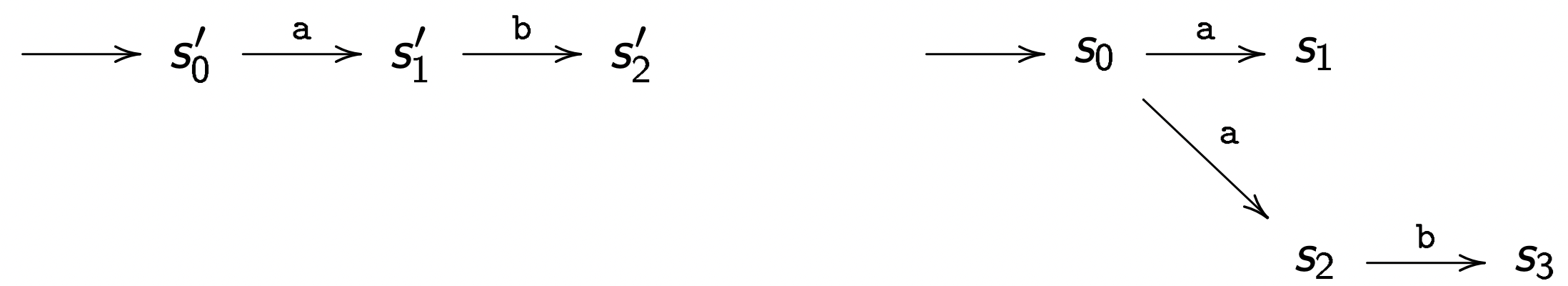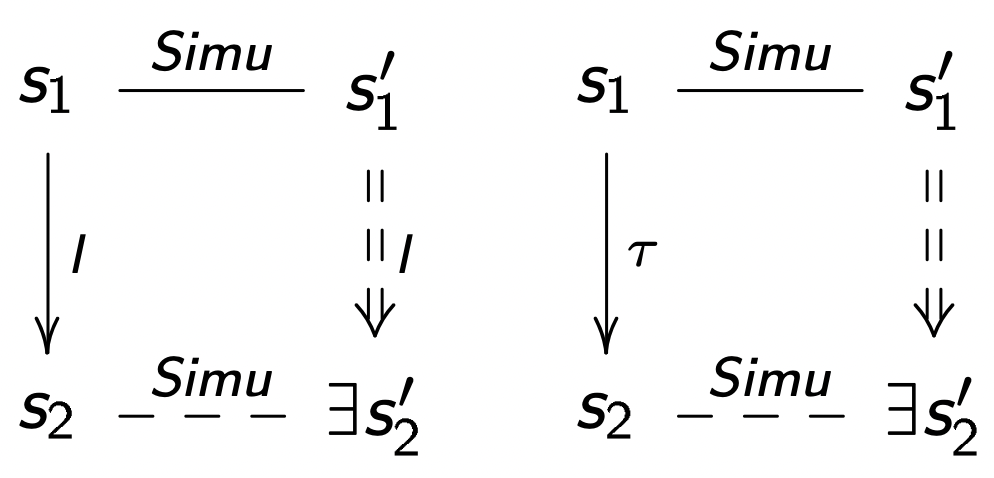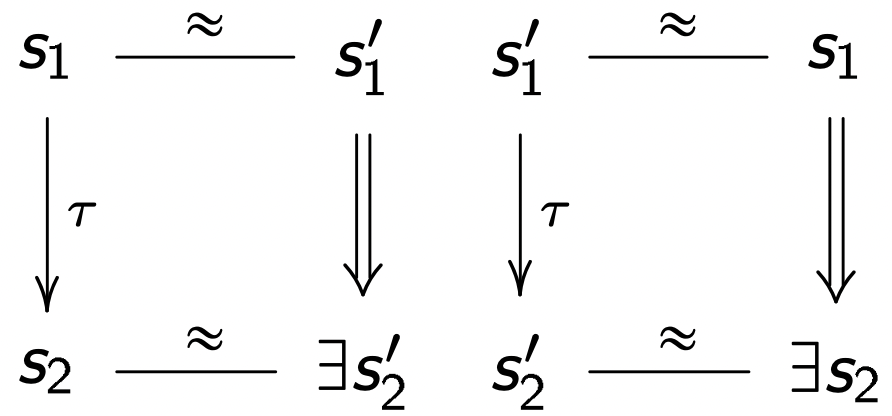写在前面:
本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第九学期课程 “Spécifications Formelles” 及以下参考资料总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考资料:
一、(Bi)Simulation
0 带标签的变迁系统
课程回顾:Transition System(变迁系统)
相比于普通的变迁系统(三元组),带标签的变迁系统是一个四元组 ⟨S,L,I,R⟩,其中:
- S 是这个系统的状态集。其可以是有限的,也可以是无限的。
- L 是这个系统的字母表(alphabet),也即整个系统的标签集。
- I 是这个系统的初始状态集,I⊆S。
- R 用来描述这个系统各个状态间的关系,R⊆S×L×S。其中 (s,l,s′)∈R 表示在状态 s 与状态 s′ 之前存在一个带有标签的事件 l,即 (s,l,s′)≜(sls′)∈R
其中,我们可以将事件分为两类:
- 可观察事件:由普通的标签表示,如 s1as2bs3
- 不可观察的内部事件:由特殊标签 τ 表示。对于观察者而言,其类似于一个黑箱,黑箱内部的标签抽象为 τ。例如 s1as4≜s1τs2τs3as4
几种特殊的关系:
- s⇒s′≜sτs1τ...τs′
- sas′≜s⇒s1as2⇒s′
1 Strong Simulation
定义
假设存在两个带标签的变迁系统(S.T.E.):S=⟨S,L,I,R⟩ 和 S′=⟨S′,L,I′,R′⟩。其中,它们有相同的标签集 L:
【定义 1】我们定义一个关系 Simu⊆S×S′,是 S′ 关于 S 的强模拟(Strong-Simulation)关系,当且仅当
\begin{align}
& \forall s_1 , s_2 \in \mathcal{S}, l \in L, s' \in \mathcal{S'} . \langle s_1 , s_1' \rangle \in Simu \land s_1 \xrightarrow{l} s_2 (\in R)\\
\Rightarrow\\
& \exist s_2'.\langle s_2,s_2' \rangle \in Simu \land s_1' \xrightarrow{l} s_2' (\in R')
\end{align}
如图所示,Simu 关系将 S 的状态与 S′ 状态联系起来成为可能。这两个系统可以做相同(或更多)的事情,即至少以相同的方式相同多的事件。
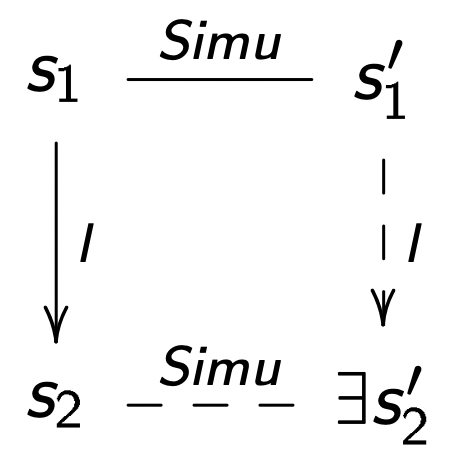
满足强模拟关系的两个系统 S(i∈I,s∈S) 和 S′(i′∈I′,s′∈S′) 中的状态 s,s′(包括初始状态 i.i′)可以用如下形式表示:
⟨s,s′⟩∈Simu∀i∈I.∃i′∈I′.⟨i,i′⟩∈Simu
例一
【对于关系 S×S′】
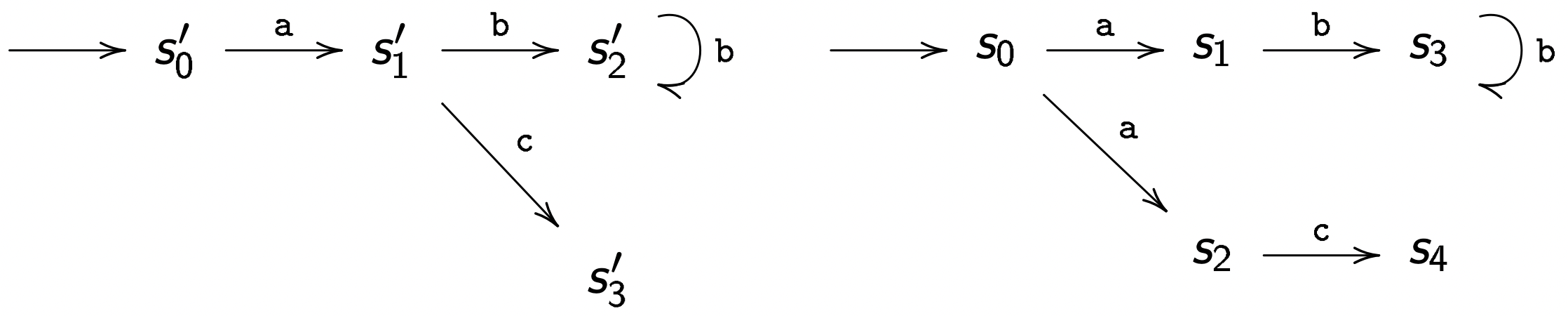
如上图,当 ⟨s0,s0′⟩∈Simu 时,S′ 可以模拟 S 。我们可以确定如下的关系 R(并不唯一):
R≜{⟨s0,s0′⟩,⟨s1,s1′⟩,⟨s2,s1′⟩,⟨s3,s2′⟩,⟨s4,s3′⟩}
- 该关系集合中包含初始状态对 ⟨s0,s0′⟩;
- 满足强模拟关系的定义
我们也可以根据以上的关系集合 R 作出如下所示的图:
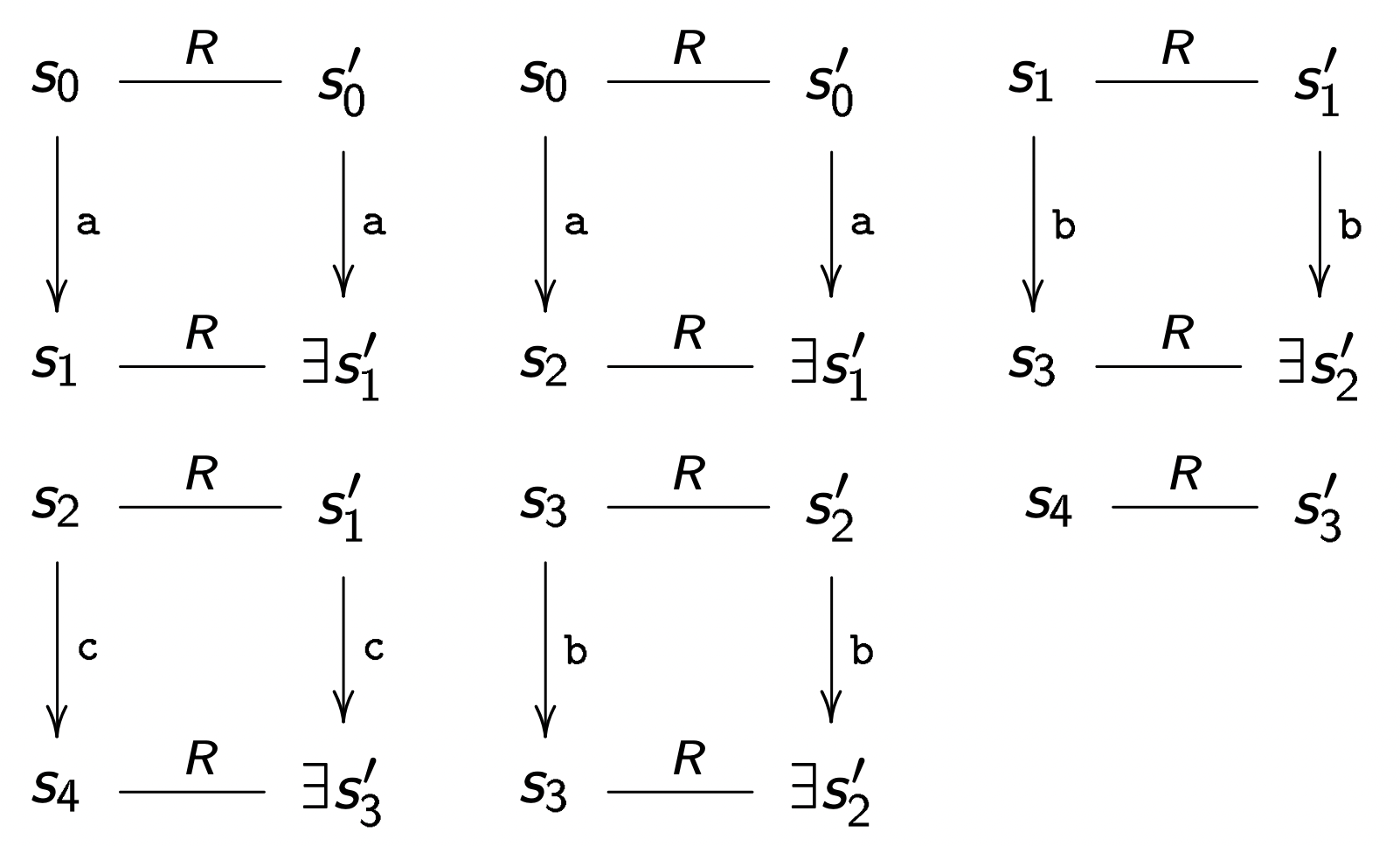
【对于关系 S′×S】
下面我们考虑关系 S′×S,当 ⟨s0′,s0⟩∈Simu 时:
可以发现,在【定义 1】中描述了 ∃s2′.⟨s2,s2′⟩∈Simu∧s1′ls2′。在关系 S′×S 中,我们考虑 ⟨s1′,s1⟩ 或 ⟨s1′,s2⟩,二者只能取其一。无论选取 S 中的哪一个分支,都有另一个分支的状态被“丢弃”。
所以,关系 S′×S 并不是强模拟关系,但是他们之中有符合强模拟关系的子系统。
性质
算术性质
我们将考虑关于系统 S×S 的如下关系:
-
空关系:空关系 ∅ 也是强模拟关系。
-
自反性:任何系统都与它自身存在强模拟关系。
-
传递性:如果关系 R⊆S×S′ 和 R′⊆S′×S′′ 是两个模拟关系,那么 S×S′′ 也存在模拟关系:
R;R′≜{⟨s,s′′⟩∣∃x′∈S.⟨s,s′⟩∈R∧⟨s′,s′′⟩∈R′}
-
并集:如果关系 R 和 R′ 都是模拟关系,那么他们的并集 R∪R′ 也是模拟关系。
-
克莱尼(Kleene)闭包:如果关系 R 是模拟关系,那么其克莱尼闭包 R∗ 也是模拟关系:
R∗≜i∈N⋃Ri,其中Ri≜R;⋯;R (i个R)
最大强模拟
我们通过在同一个字母表 L 上定义 S′ 对于 S 的最大模拟(Plus grande simulation)关系。存在这种关系的原因在于:
- 两个模拟关系的并集可以组成一个更大的模拟关系;
- 他们之间的所有模拟关系都以 S×S′ 为界;
如果 S 与 S′ 都是有限的系统,那么:
- 最大模拟关系是可以计算的;
- 任何关于「s′ 能否模拟 s」的问题都可以通过转化成最大模拟关系来解决。
我们用 S≺S′ 来表示这种关系。
【组合性(Compositionalité)】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′,我们假设它们之间存在强模拟关系。对于任何包含子系统 S 的系统 G,G[S′] 都可以模拟 G[S]。
SsimuS′得出G[S]simuG[S′]
【迹】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′,我们假设它们之间存在强模拟关系。我们可以得出:
Prefix(Exec(S))⊆Prefix(Exec(S′))Prefix(Trace(S))⊆Prefix(Trace(S′))
证明模拟关系
对于两个有限的系统 S 和 S′,我们可以:
- 计算系统 S 和 S′ 之间的最大强模拟关系;
- 检查是否包含初始状态。
【定义 2】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′, S′ 对 S 的最大强模拟是以下关系 Ri,i∈N 的极限(递减):
{R0Ri+1≜S×S′≜Ri∩F(Ri)
其中,
\begin{align}
\mathcal{F}(R_i) \triangleq
& \{ \langle s_1, s_1' \rangle \mid \forall l \in L. \forall s_2 \in S. \\
& (s_1 \xrightarrow{l} s_2 \Rightarrow \exist s_2' \in S'.s_1' \xrightarrow{l} s_2' \land \langle s_2,s_2'\rangle \in R) \}
\end{align}
例一
与之前的例子相同,我们来证明 S×S′ 是强模拟的。

根据【定义 2】,我们可以迭代计算出如下的最大强模拟关系 Ri,i∈N
\begin{align}
R_0 \quad = \quad & S \times S' \\
= \quad & \{ \langle s_0, s_0' \rangle , \langle s_0, s_1' \rangle , \langle s_0, s_2' \rangle , \langle s_0, s_3' \rangle \\
& ,\langle s_1, s_0' \rangle , \langle s_1, s_1' \rangle , \langle s_1, s_2' \rangle , \langle s_1, s_3' \rangle \\
& ,\langle s_2, s_0' \rangle , \langle s_2, s_1' \rangle , \langle s_2, s_2' \rangle , \langle s_2, s_3' \rangle \\
& ,\langle s_3, s_0' \rangle , \langle s_3, s_1' \rangle , \langle s_3, s_2' \rangle , \langle s_3, s_3' \rangle \} \\
& ,\langle s_4, s_0' \rangle , \langle s_4, s_1' \rangle , \langle s_4, s_2' \rangle , \langle s_4, s_3' \rangle \} \\
R_1 \quad = \quad & \{ \langle s_0, s_0' \rangle , \langle s_1, s_1' \rangle , \langle s_1, s_2' \rangle \\
& ,\langle s_2, s_1' \rangle \\
& , \langle s_3, s_1' \rangle , \langle s_3, s_2' \rangle \} \\
& ,\langle s_4, s_0' \rangle , \langle s_4, s_1' \rangle , \langle s_4, s_2' \rangle , \langle s_4, s_3' \rangle \} \\
R_2 \quad = \quad & R_1
\end{align}
所以,R2 是关系 S×S′ 上的最大强模拟,我们有:
\begin{align}
s_0 \prec & \; s_0' \\
s_1,s_3 \prec & \; s_1',s_2' \\
s_2 \prec & \; s_1' \\
s_4 \prec & \; s_0',s_1',s_2',s_3' \\
\end{align}
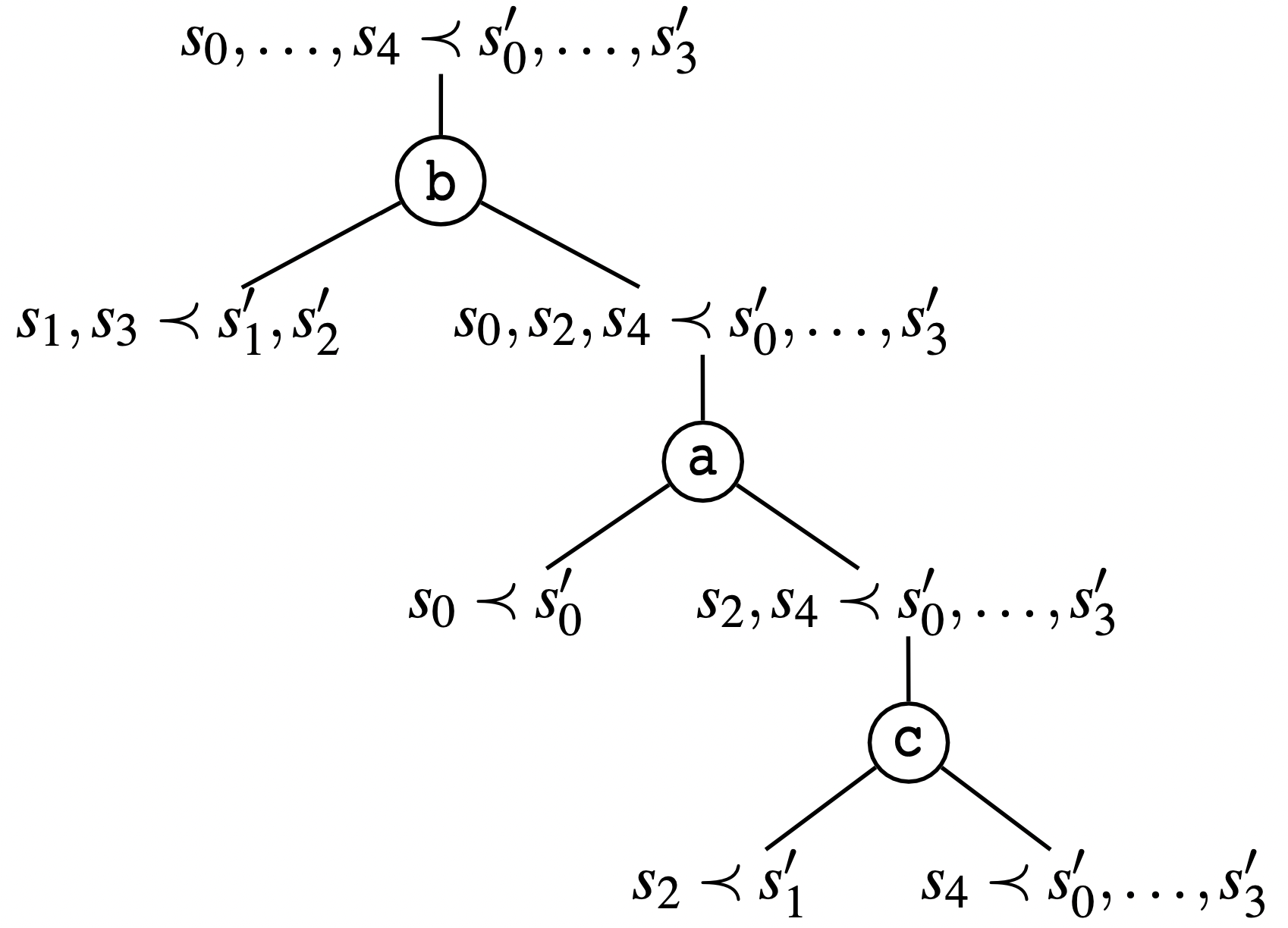
【树状形式】我们更希望使用树状形式更直观地显示最大强模拟 Ri 的推理。
提醒 ⚠️:在下图中
- 我们可以使用类似自动机的“概念”来消费这个字母表 L,即下图中圆圈中的字母 li∈L;
- 在 S.T.E. 系统 S 中,有一个状态 si 通过消费字母 li 迁移到系统 sj,即 silisj;
- 在另一个有着相同字母表 L 的 S.T.E. 系统 S′ 中,有 sn′lism′;
- 我们可以写出如下的关系:si≺sn′,并将其放在左子树,其余部分则在右子树。
- 重复以上步骤,直到 “≺ 关系” 不再改变。
2 Strong Bi-Simulation
定义
双模拟(BiSimulation)系统之间的一种基本关系,用来表示两个系统之间的等价性。但是以下条件不能推导出 BiSimulation 关系:
S simulate S′∧S′ simulate S≡S Bi-Simulate S′
下面我们给出强双模拟的定义:
【定义 3】
对于两个系统 S 和 S′,我们在 (S×S′)∪(S′×S) 上定义双模拟关系 R ,使得:
- R 是 (S×S′)∪(S′×S) 上的强模拟关系;
- R 是一种对称关系;
- 实际上,两个存在双模拟关系的系统在同一时间做相同的事情。
例二
我们考虑以下两个系统:
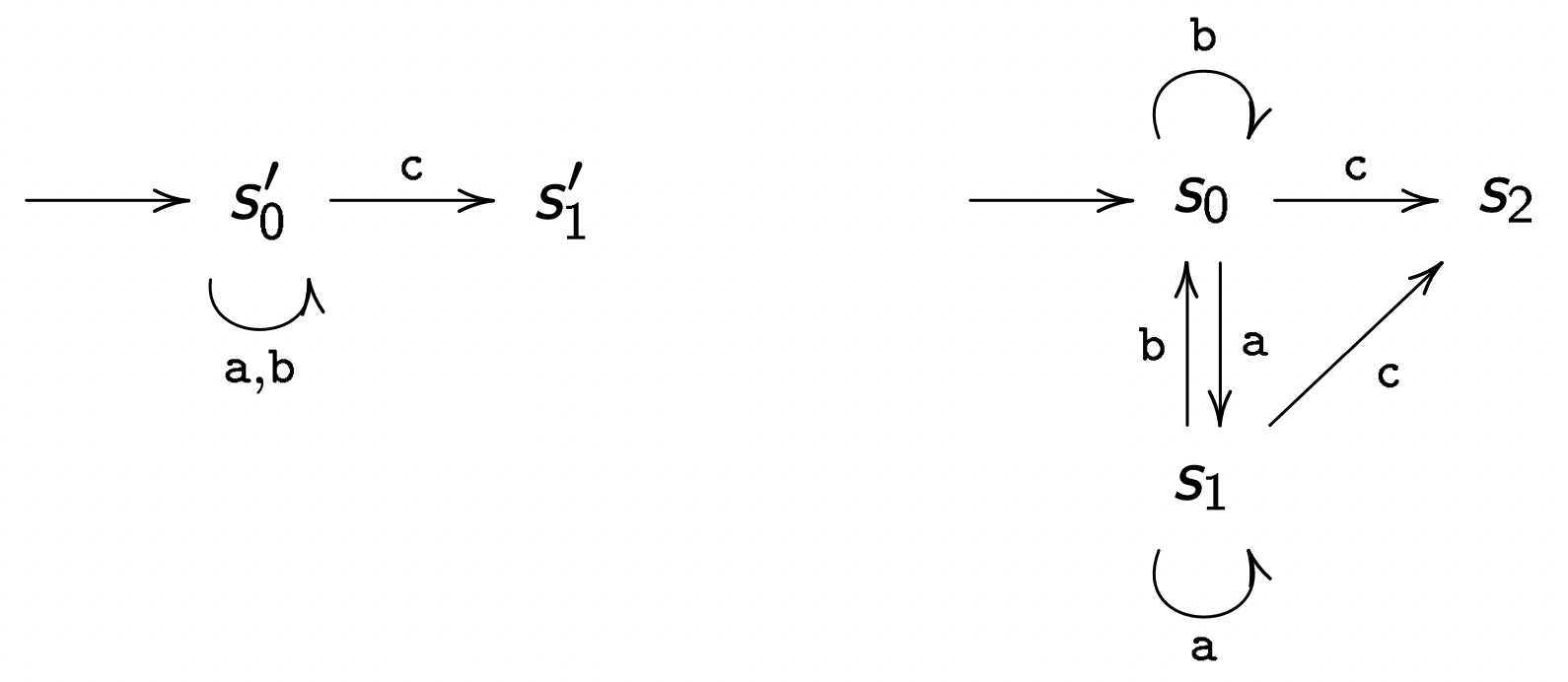
一个可能的(强)双模拟关系为:
R≜{⟨s0,s0′⟩,⟨s1,s0′⟩,⟨s2,s1′⟩,⟨s0′,s0⟩,⟨s0′,s1⟩,⟨s1′,s2⟩}
有上述结果可以看出,双模拟关系是对称的。
例三
我们再考虑另外两个系统:
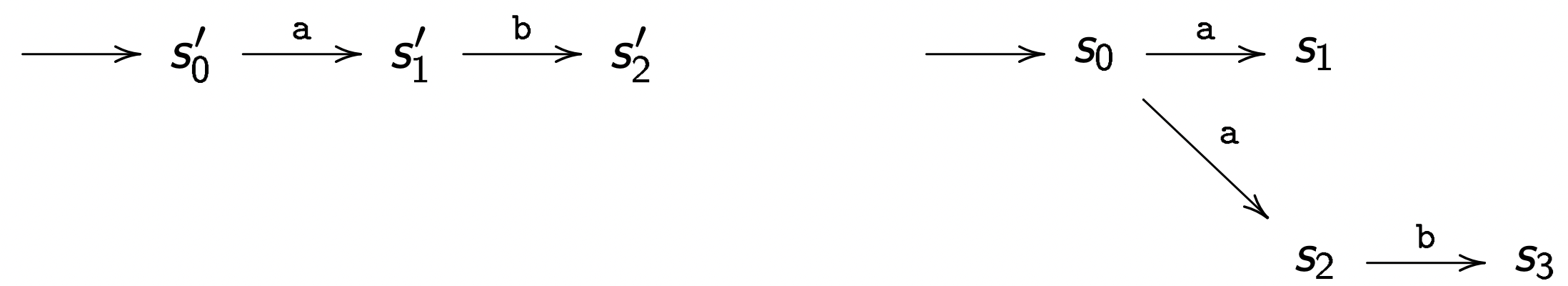
我们可以找到如下(强)模拟关系:
-
S′ simulate S:
R1≜{⟨s0,s0′⟩,⟨s1,s1′⟩,⟨s2,s1′⟩,⟨s3,s2′⟩}
-
S simulate S′:
R2≜{⟨s0′,s0⟩,⟨s1′,s2⟩,⟨s2′,s3⟩}
-
但是 S 和 S′ 并不是(强)双模拟关系
性质
算数性质
- 双模拟(BiSimulation)有着模拟(Simulation)的所有算数性质;
- 此外,任何双模拟都是对称的(即 Ri=Ri−1),它是一个等价的关系。
最大强双模拟
我们通过在同一个字母表 L 上定义 S 和 S′ 之间的最大强双模拟(Plus grande BiSimulation)关系。存在这种关系的原因在于:
- 两个双模拟关系的并集可以组成一个更大的双模拟关系;
- 他们之间的所有双模拟关系都以 (S×S′)∪(S′×S) 为界;
如果 S 与 S′ 都是有限的系统,那么:
- 最大双模拟关系是可以计算的;
- 任何关于「s′ 与 s 是否是双模拟关系」的问题都可以通过转化成最大双模拟关系来解决。
我们用 S∼S′ 来表示这种关系。
【组合性(Compositionalité)】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′,我们假设它们之间存在强模拟关系。对于任何包含子系统 S 的系统 G,G[S′] 都可以模拟 G[S]。
S∼S′得出G[S]∼G[S′]
【迹】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′,我们假设它们之间存在强模拟关系。我们可以得出:
Exec(S)=Exec(S′)Trace(S)=Trace(S′)
证明模拟关系
与之前的模拟关系类似,对于两个有限的系统 S 和 S′,我们可以:
- 计算系统 S 和 S′ 之间的最大双模拟关系;
- 检查是否包含初始状态。
【定义 4】
对于两个在同一个字母表 L 上定义的 T.S.E. 系统 S 和 S′, S′ 对 S 的最大双模拟是以下关系 Ri,i∈N 的极限(递减):
{R0Ri+1≜(S×S′)∪(S′×S)≜Ri∩F(Ri)∩F(Ri)−1
其中,
\begin{align}
\mathcal{F}(R_i) \triangleq
& \{ \langle s_1, s_1' \rangle \mid \forall l \in L. \forall s_2 \in S \cup S'. \\
& (s_1 \xrightarrow{l} s_2 \Rightarrow \exist s_2' \in S \cup S'.s_1' \xrightarrow{l} s_2' \land \langle s_2,s_2'\rangle \in R_i) \}
\end{align}
例三
与之前的【例三】相同,我们来证明 R=(S×S′)∪(S′×S) 是强双模拟的。
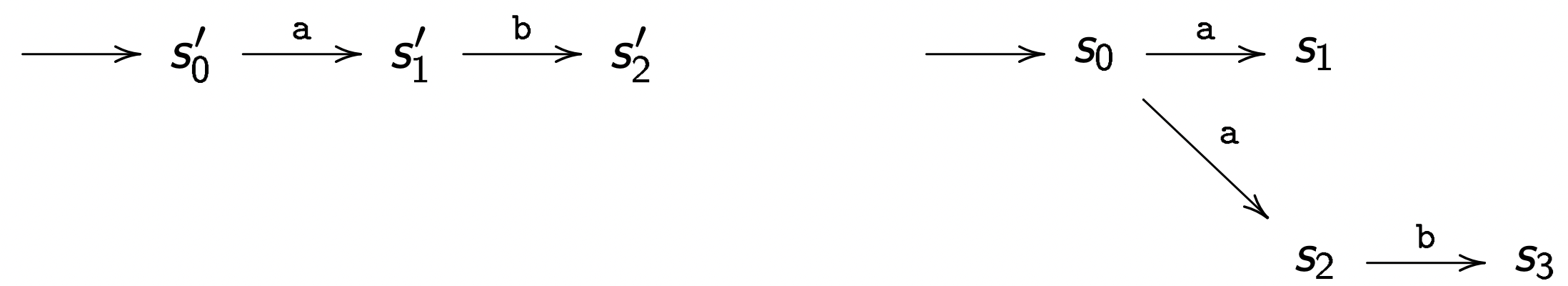
根据【定义 4】,我们可以迭代计算出如下的最大强模拟关系 Ri,i∈N
\begin{align}
R_0 \quad = \quad & (\mathcal{S} \times \mathcal{S'}) \cup (\mathcal{S'} \times \mathcal{S}) \\
R_1 \quad = \quad & \{ \langle s_0, s_0' \rangle , \langle s_0', s_0 \rangle , \langle s_1, s_2' \rangle , \langle s_2', s_1 \rangle , \langle s_2, s_1' \rangle , \langle s_1', s_2 \rangle , \langle s_3, s_2' \rangle , \langle s_2', s_3 \rangle \} \\
R_2 \quad = \quad & \{ \langle s_1, s_2' \rangle , \langle s_2', s_1 \rangle , \langle s_2, s_1' \rangle , \langle s_1', s_2 \rangle , \langle s_3, s_2' \rangle , \langle s_2', s_3 \rangle \} \\
R_3 \quad = \quad & R_2
\end{align}
所以,R3 是关系 (S×S′)∪(S′×S) 上的最大双模拟,我们有:
3 Weak Simulation
前面我们提到过,事件分为两类:
- 可观察事件:由普通的标签表示,如 s1as2bs3
- 不可观察的内部事件:由特殊标签 τ 表示。对于观察者而言,其类似于一个黑箱,黑箱内部的标签抽象为 τ。例如 s1as4≜s1τs2τs3as4
在之前的强模拟关系中,我们假设所有的事件都是可观察事件,即标签 l∈L 为普通标签。
但是,对于一个用户可观察事件来讲,其中可能包含若干个不可观察事件。
例如一个加法,
- 从用户的角度观察到的事件为 x+y=z;
- 但是从机器的角度,还有“取址”等操作。但是对于用户来讲,“取址”操作是不可见的。
所以,强模拟关系在系统描述中限制太多。相对的,我们提出了弱模拟关系(Weak Simulation)。
定义
假设存在两个带标签的变迁系统(S.T.E.):S=⟨S,L,I,R⟩ 和 S′=⟨S′,L,I′,R′⟩。其中,它们有相同的标签集 L:
【定义 5】我们定义一个关系 Simu⊆S×S′,是 S′ 关于 S 的弱模拟(Weak-Simulation)关系,当且仅当
\begin{align}
\forall s_1 , s_2 \in \mathcal{S}, l \in L, s' \in \mathcal{S'} . \\
& (\langle s_1 , s_1' \rangle \in Simu \land s_1 \xrightarrow{l} s_2 (\in R) \\
& \Rightarrow \\
& \exist s_2'.\langle s_2,s_2' \rangle \in Simu \land s_1' \xRightarrow{l} s_2' (\in R')) \\
\land \quad & \\
& (\langle s_1 , s_1' \rangle \in Simu \land s_1 \xrightarrow{\tau} s_2 (\in R) \\
& \Rightarrow \\
& \exist s_2'.\langle s_2,s_2' \rangle \in Simu \land s_1' \Rightarrow s_2' (\in R')) \\
\end{align}
如图所示,Simu 关系将 S 的状态与 S′ 状态联系起来成为可能。
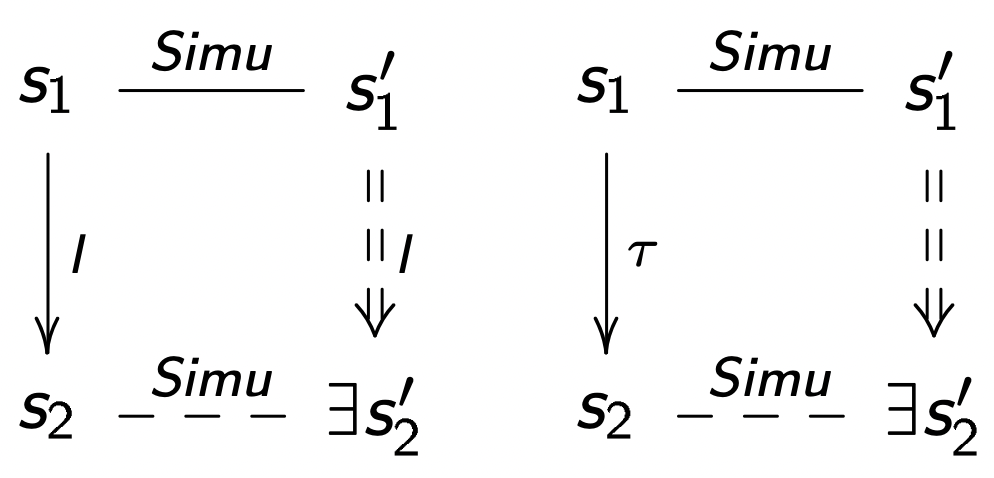
满足弱模拟关系的两个系统 S(i∈I,s∈S) 和 S′(i′∈I′,s′∈S′) 中的状态 s,s′(包括初始状态 i.i′)可以用如下形式表示:
⟨s,s′⟩∈Simu∀i∈I.∃i′∈I′.⟨i,i′⟩∈Simu
例四
假设有如下两个系统 S 和 S′:
\begin{align}
\mathcal{S}: \quad & \to s_0 \xrightarrow{a} s_1 \xrightarrow{b} s_2 \\
\mathcal{S'}: \quad & \to s_0' \xrightarrow{\tau} s_1' \xrightarrow{a} s_2' \xrightarrow{\tau} s_3' \xrightarrow{b} s_4'\\
\end{align}
-
S′ 弱模拟于 S:
R≜{⟨s0,s0′⟩,⟨s1,s2′⟩,⟨s2,s4′⟩}
注意 ⚠️:该结果并不唯一,比如我们可以添加 ⟨s1,s3′⟩ 对。
-
相反地,S 弱模拟于 S′:
R≜{⟨s0′,s0⟩,⟨s1′,s0⟩,⟨s2′,s1⟩,⟨s3′,s1⟩,⟨s4′,s2⟩}
-
事实上,S 和 S′ 在这里是弱双模拟(Weak BiSimulation)的。
例五
假设有如下两个系统 S,S′ 和 S′′:
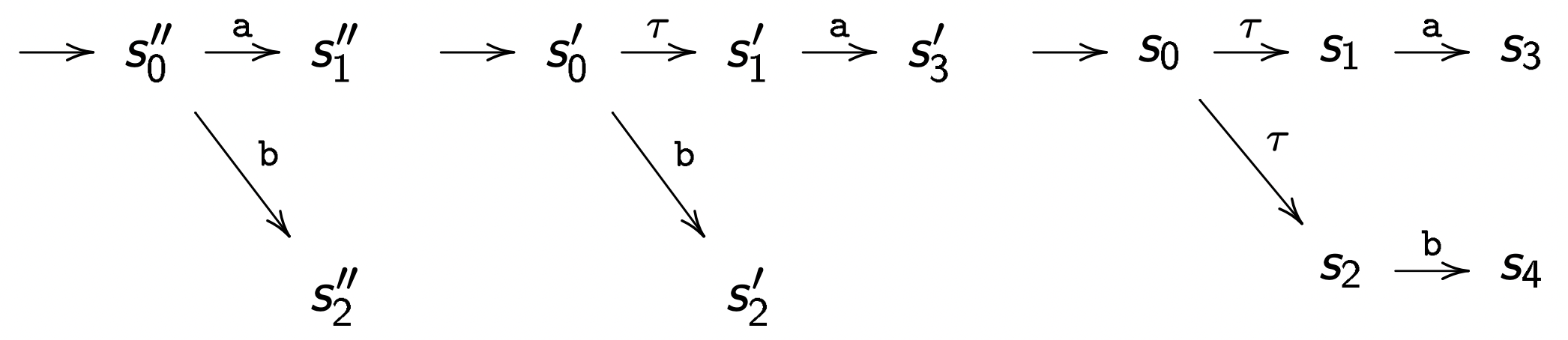
-
S′′ 弱模拟于 S′:
R≜{⟨s0′,s0′′⟩,⟨s1′,s0′′⟩,⟨s2′,s2′′⟩,⟨s3′,s1′′⟩}
-
S′ 弱模拟于 S:
R≜{⟨s0,s0′⟩,⟨s1,s1′⟩,⟨s2,s0′⟩,⟨s3,s3′⟩,⟨s4,s2′⟩}
性质
-
弱模拟(Weak-Simulation)有着与强模拟(Strong-Simulation)相同的算数性质;
-
类似的,弱模拟(Weak-Simulation)也存在最大弱模拟关系(plus grande simulation faible);
-
弱模拟的组合性要比之前的强模拟低得多。在一般情况下,不能使用另一个弱模拟的子系统来替换原来的子系统。即
Sweak−simuS′不能得出结论G[S]weak−simuG[S′]
-
关于迹(Trace):我们将 τ 统一转化成 ϵ;
-
【最大弱模拟】可以按照与[最大强模拟](# 最大强模拟)相同的规则计算,并使用【定义 6】替换定义 2。
4 Weak Bi-Simulation
定义
下面我们给出弱双模拟(Weak Bi-Simulation)的定义:
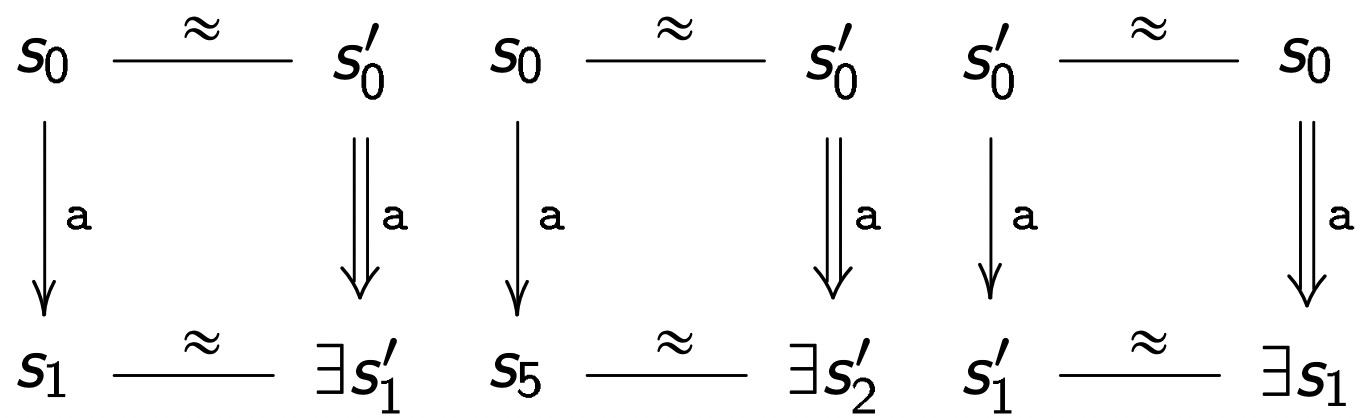
【定义 6】对于两个系统 S 和 S′,我们在 (S×S′)∪(S′×S) 上定义弱双模拟关系 R ,使得:
- R 是 (S×S′)∪(S′×S) 上的强模拟关系;
- R 是一种对称关系;
- 我们用 【S≈S′】 来表示这种关系。
例六
假设有如下两个定义在相同字母表 L 的 S.T.E. 系统 S 和 S′:
\begin{align}
\mathcal{S}: \quad & \to s_0 \xrightarrow{a} s_1 \\
\mathcal{S'}: \quad & \to s_0' \xrightarrow{\tau} s_1' \xrightarrow{a} s_2' \\
\end{align}
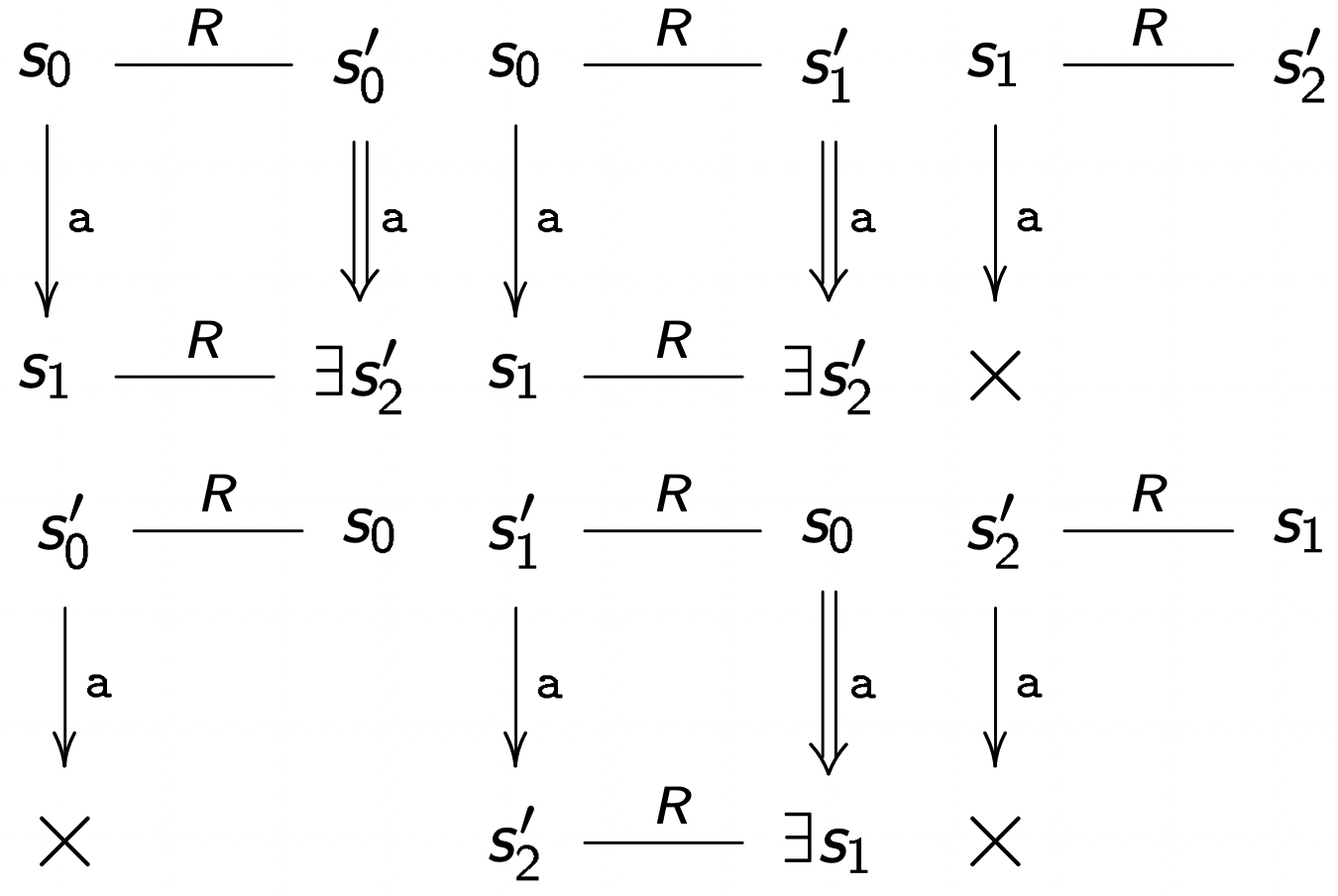
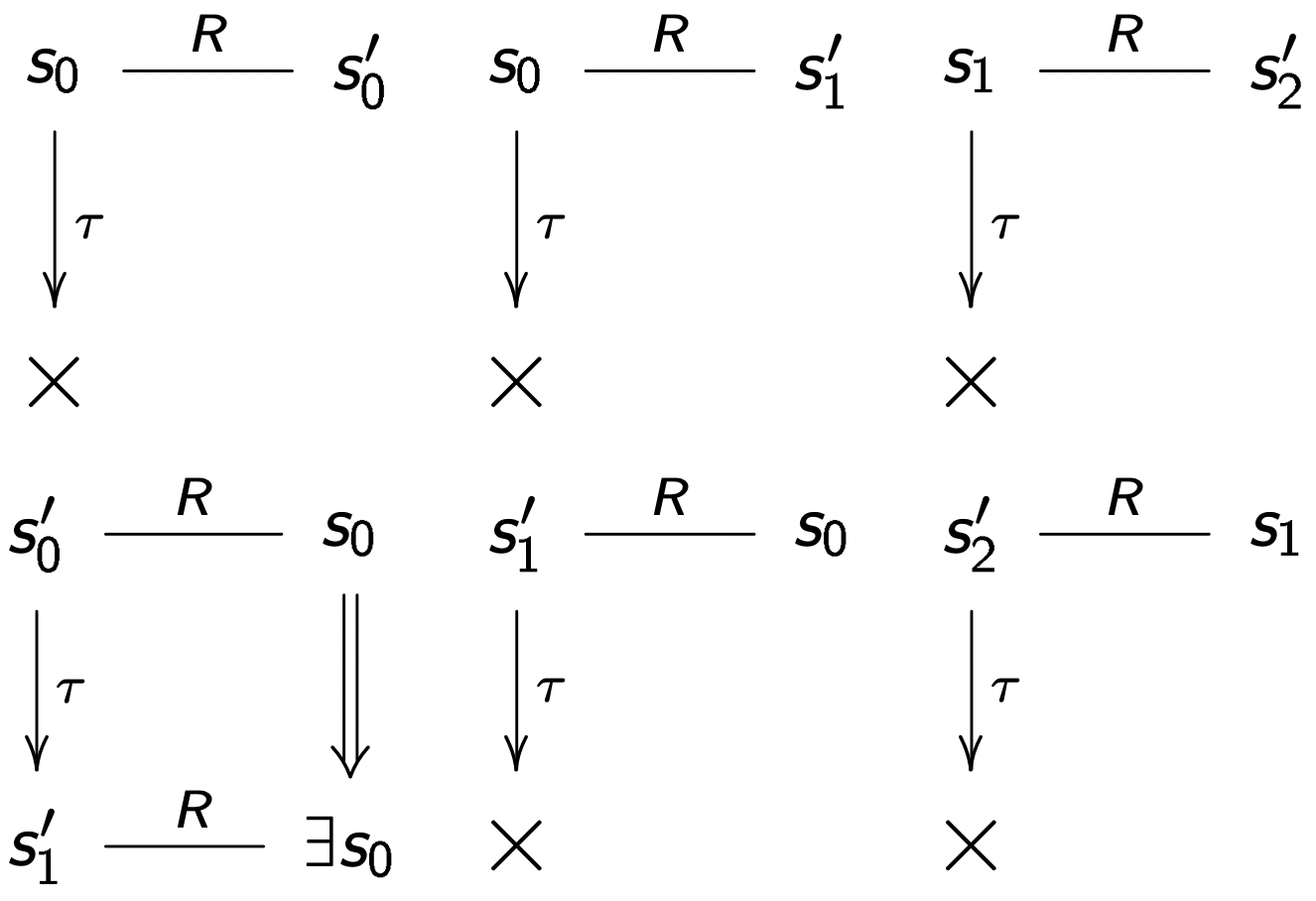
S 与 S′ 是弱双模拟的,模拟关系如下所示:
R≜{⟨s0,s0′⟩,⟨s0′,s0⟩,⟨s0,s1′⟩,⟨s1′,s0⟩,⟨s1,s2′⟩,⟨s2′,s1⟩}
例七
假设有如下两个定义在相同字母表 L 的 S.T.E. 系统 S 和 S′:
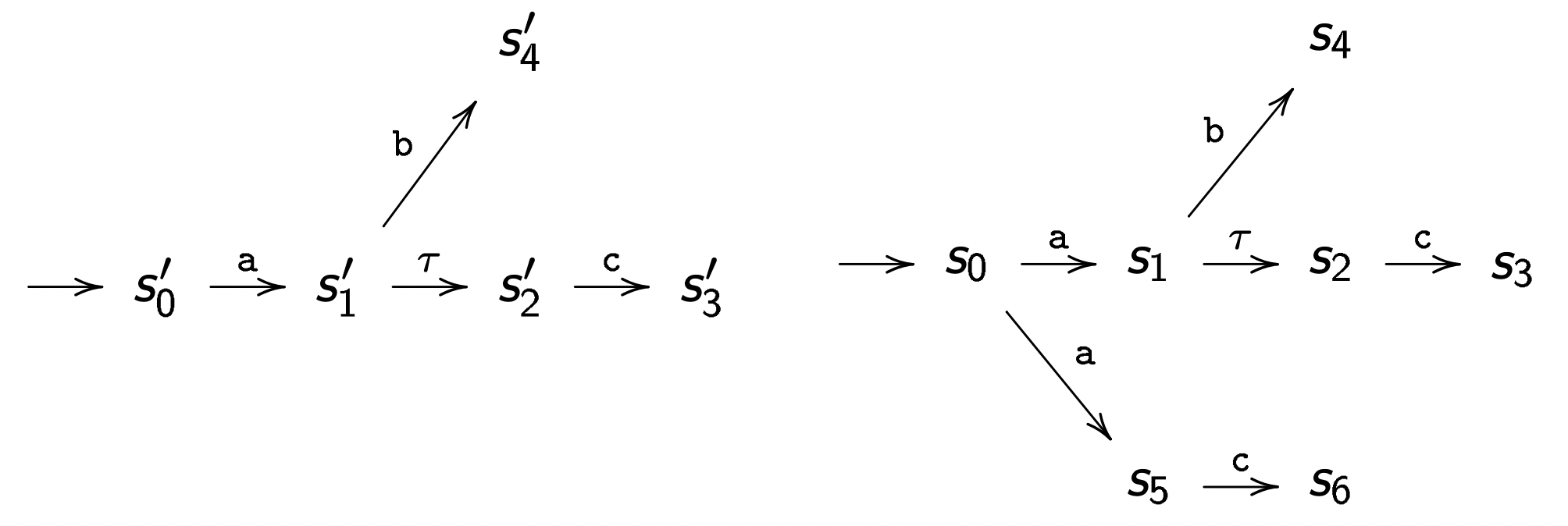
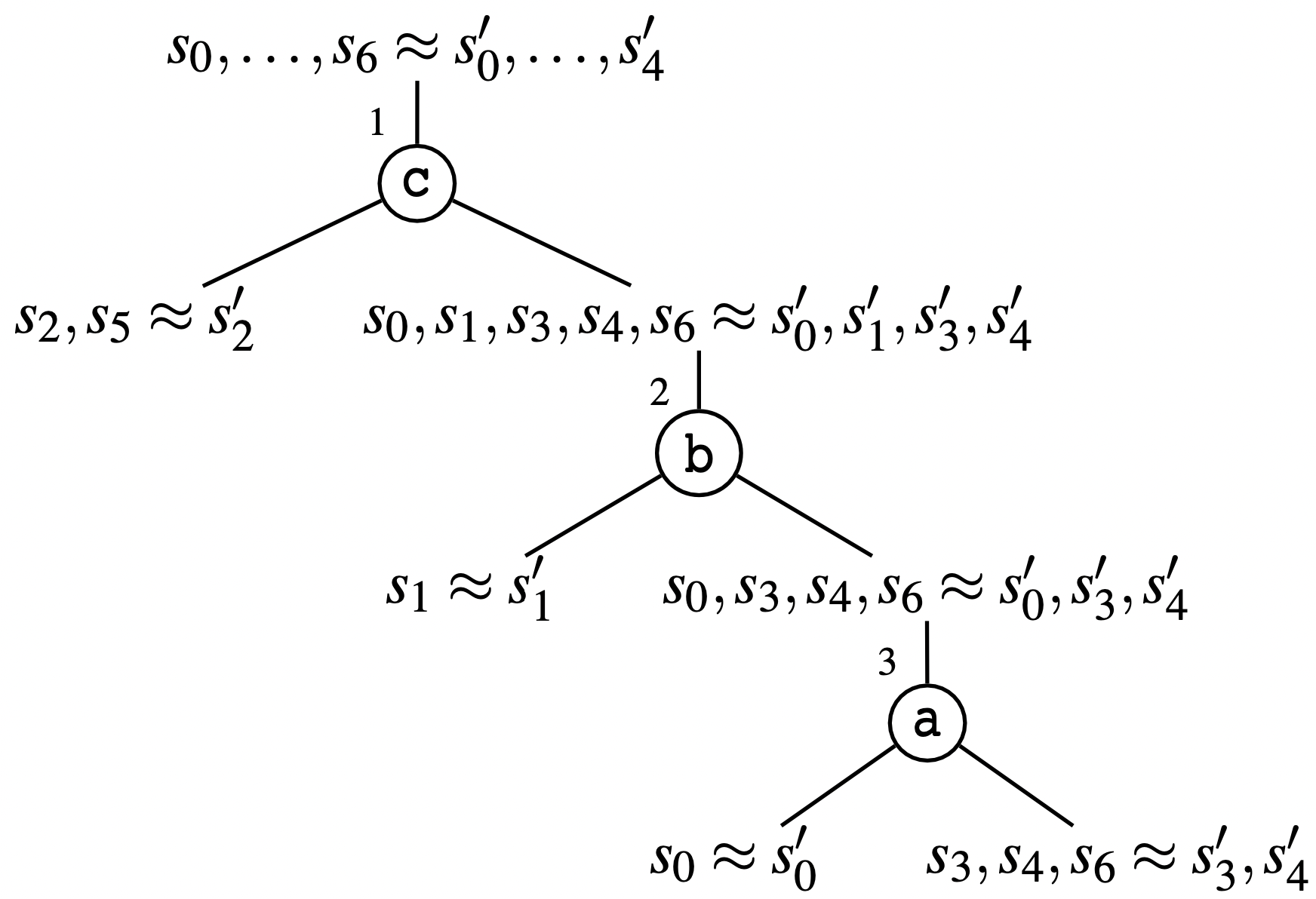
S 与 S′ 是弱双模拟的,我们可以以树的形式证明:
二、CCS
0 前情
随着计算机网络的出现和广泛应用,一个问题由此显现:通信系统与我们大多数人熟悉的计算系统有着根本的不同;用来建模传统计算系统的工具未能捕捉到分布式世界中许多计算的相关特性(缺少相关的模型)。
所以有些人便开始寻找更有用、更现实的方式来描述 Communicating Systems,这便是:process calculus (或者叫: process algèbres)。
CSS (Calculus of Communicating System) 就是其中的一种理论基础。
1 相关性质
Syntax
-
事件语言 L 包含成对的称为动作 A 的互补事件 A,以及 τ 事件:
L≜{τ}∪A∪A
其中:
- A 是一个动作(Action)集,其对应接收消息的事件(Event);
- A≜{a∣a∈A} 是事件集 A 的互补事件集合,其对应发送消息的事件(Event)。
-
CSS 术语(Termes)由如下语法描述:
-
P::=0:表示已经结束的过程 P(非活动进程);
-
P::=l.P1:表示一个过程的前缀(Prefix),我们先执行事件 l∈L,然后执行P1;
-
P::=P1∥P2:并行结构,表示两个 Pi 同步地执行;
(1)我们先找到 ∥ 两端的过程 P 中事件字母表 L 中相交的集合 Θ
(2)当 ∥ 两端的任意一个过程 P 执行到 Θ 中的元素 lθ时,都会检查是否其他过程也可以执行该元素 lθ;
(3)如果可以,则两端的过程同时执行元素 lθ;
(4)如果不可以,则暂停本端执行,直到另一端执行到该元素 lθ。
【例子】b.a.c.0∥d.e.a.0,Θ={a}
graph TD
b.a.c.0//d.e.a.0 --b--> a.c.0//d.e.a.0
b.a.c.0//d.e.a.0 --d--> b.a.c.0//e.a.0
a.c.0//d.e.a.0 --d-->a.c.0//e.a.0
a.c.0//e.a.0 --e--> a.c.0//a.0
a.c.0//a.0 --a-->c.0
a.c.0//a.0 --a-->0
c.0 --c--> 0
b.a.c.0//e.a.0 --b--> a.c.0//e.a.0
b.a.c.0//e.a.0 --e--> b.a.c.0//a.0
b.a.c.0//a.0 --b--> a.c.0//a.0
-
P::=P1+P2:选择结构,表示在两个 Pi 中选择一个执行;
-
P11::=va.P:给 P1 声明一个局部“canal”。
-
如下语法描述了使用方程组形式来定义过程(可以是递归形式的):
{Xi≜Ei}
其中,Ei 是过程 Xi 中涉及变量的 CCS 术语(Termes)。
- 此约束允许存在唯一解;
- CCS 的过程就是 Xi;
- 这个定义是被“保护的”,其定义的形式如下
-
CCS 程序 G 是一组过程 P 的定义:
- G::=D∣DG
- D::=X≜P
- P::=0∣l.P∣P∥P∣P+P∣va.P
- P′::=X∣0∣l.P′∣P′∥P′∣P′+P′∣va.P′
-
正确的定义:
X≜a.XX≜a.0∥b.XX≜a.(b.0∥X)
-
错误的定义:
X≜XX≜a.0+(b.0∥X)
例一
假设有如下两个定义在相同字母表 L 的 S.T.E. 系统 S 和 S′:

它们可以通过以下两个 CCS 过程表示:
- P′≜a.(b.0+τ.c.0)
- P≜a.(τ.c.0+b.0)+a.c.0
例二
我们模拟一下投币式自动售货机:我们可以用 20 分买到茶(tea)和咖啡(coffee);用 40 分买到卡布奇诺(cappuccino)。售货机只接收 10 分和 20 分的硬币。我们对售货机 Machine 进行建模:
- Machine≜20.Service1+10.10.Service1
- Service1≜coffee.Machine+tea.Machine+20.Service2+10.10.Service2
- Service2≜cappuccino.Machine
同样的,我们也可以对用户进行建模,假设用户 User 用了两个 10 分的硬币买了一杯咖啡:
- User≜10.10.coffee.0
Semantic
- 我们为 CCS 定义了一个操作语义 (Semantic),即我们对于每个 CCS 过程定义了一个 S.T.E.。
- 为了简化转换的描述,我们确定了某些等价项(例如,A+B≡B+A)。这种等价关系实际上是对CCS 运算符的同余 (Congruence)。
同余 Congruence
对于一个给定的 process algèbres 来说,同余 (Congruence) 是一个与该 process algèbres 的算子相换的等价物。
【定义 5】CCS 的过程 (Process) 之间的等价 ≅是同余的,当且仅当,对于所有过程,如 P≅Q,我们有:
- a.P≅a.Q
- P+M≅Q+M 或 M+P≅M+Q
- P∥M≅Q∥M 或 M∥P≅M∥Q
- va.P≅va.Q
结构同余 Structural Congruence
【定义 6】结构同余 P≡Q 是由以下规则决定的。它符合【定义 5】的条件:
- 通过 α−conversion 改变“canal”名称:如果 b 没有出现在 P 中,那么 va.P≡vb.P[a←b]
- “+” 满足交换律和结合率:P+Q≡Q+P 和 P+(Q+R)≡(P+Q)+R≡P+Q+R
- “∥” 的阿贝尔幺半群定律 (Abelian monoid law):P∥0≡P、P∥Q≡Q∥P、P∥(Q∥R)≡(Q∥P)∥R≡Q∥P∥R
- va.0≡0、va.vb.P≡vb.va.P