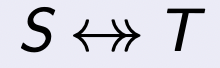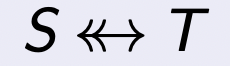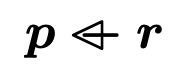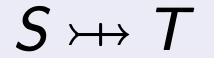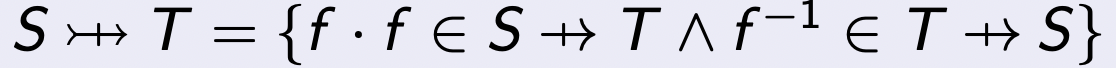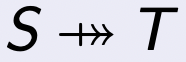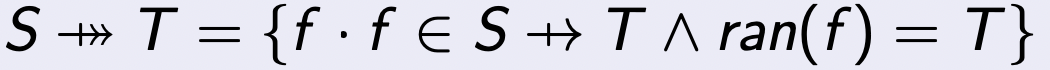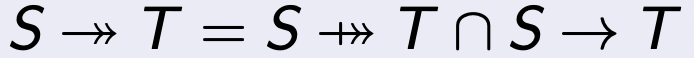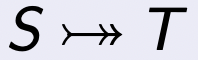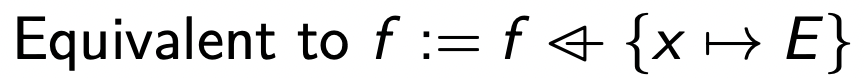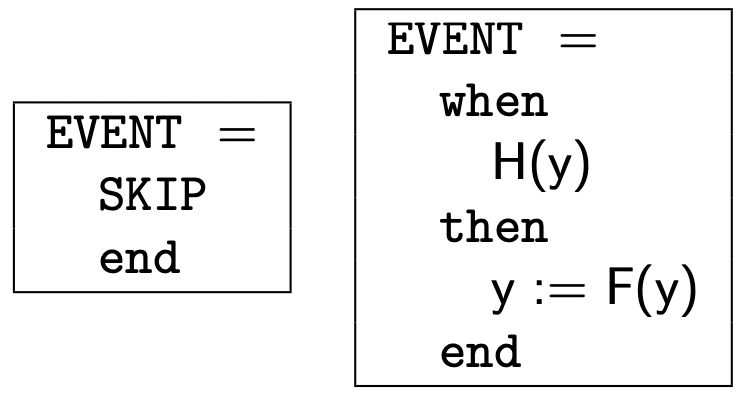写在前面:
本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T. ) 第九学期课程 “Formal development of complex system” 及以下参考资料总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考资料:
在软件工程的生命周期中,有一部分非常重要的工作,那就是进行需求分析 需求文档
需求分析 需求文档
形式化语言常用于软件工程生命周期的需求分析阶段,可以帮助工程师理解需求文档,完成建模(需求到形式化模型的转换),甚至进一步完善需求文档(挖掘隐藏的需求,以及改进需求中矛盾的部分)。
因此,我们在正式介绍 Event-B 这种形式化方法之前,需要先了解一些关于集合论的概念,以及其他的相关知识。
为了描述软件系统中的事实,就需要写各种各样的谓词(Predicate),也就是对事实的表述的断言。
我们不但需要描述一些简单的事实,还可能需要描述非常复杂的事实。为此就需要谓词逻辑表示为描述软件的性质。下面给出几个基础的谓词逻辑的表达形式:
数学表示
说明
⊤ \top ⊤ TRUE,永真(Constant True)
⊥ \bot ⊥ FALSE,永假(Constant False)
¬ A \neg A ¬ A 否定(Negation)
A ∧ B A \land B A ∧ B 和取(Conjunction)
A ∨ B A \lor B A ∨ B 析取(Disjunction)
A ⇒ B A \Rightarrow B A ⇒ B 蕴含(Implication)
A ⇔ B A \Leftrightarrow B A ⇔ B 等价(Equivalence)
在谓词逻辑(和命题逻辑)里可以证明大量的等价公式 谓词演算 等价
谓词演算
说明
P ⇒ Q = ¬ P ∨ Q P \Rightarrow Q \quad = \quad \neg P \lor Q P ⇒ Q = ¬ P ∨ Q
P ⇔ Q = ( P ⇒ Q ) ∧ ( Q ⇒ P ) P \Leftrightarrow Q \quad = \quad (P \Rightarrow Q) \land (Q \Rightarrow P) P ⇔ Q = ( P ⇒ Q ) ∧ ( Q ⇒ P )
P ∧ P = P P \land P \quad = \quad P P ∧ P = P ∧ \land ∧
P ∨ P = P P \lor P \quad = \quad P P ∨ P = P ∨ \lor ∨
P ∧ ¬ P = ⊥ ( FALSE ) P \land \neg P \quad = \quad \bot(\text{FALSE}) P ∧ ¬ P = ⊥ ( FALSE ) 矛盾律
P ∨ ¬ P = ⊤ ( TRUE ) P \lor \neg P \quad = \quad \top(\text{TRUE}) P ∨ ¬ P = ⊤ ( TRUE ) 排中律
P ∧ ⊤ = P P \land \top \quad = \quad P P ∧ ⊤ = P
P ∧ ⊥ = ⊥ P \land \bot \quad = \quad \bot P ∧ ⊥ = ⊥
P ∨ ⊤ = ⊤ P \lor \top \quad = \quad \top P ∨ ⊤ = ⊤
P ∨ ⊥ = P P \lor \bot \quad = \quad P P ∨ ⊥ = P
P ∧ Q = Q ∧ P P \land Q \quad = \quad Q \land P P ∧ Q = Q ∧ P ∧ \land ∧
P ∨ Q = Q ∨ P P \lor Q \quad = \quad Q \lor P P ∨ Q = Q ∨ P ∨ \lor ∨
( P ∧ Q ) ∧ R = Q ∧ ( P ∧ R ) (P \land Q) \land R \quad = \quad Q \land (P \land R) ( P ∧ Q ) ∧ R = Q ∧ ( P ∧ R ) ∧ \land ∧
( P ∨ Q ) ∨ R = Q ∨ ( P ∨ R ) (P \lor Q) \lor R \quad = \quad Q \lor (P \lor R) ( P ∨ Q ) ∨ R = Q ∨ ( P ∨ R ) ∨ \lor ∨
P ∧ ( Q ∨ R ) = ( P ∧ Q ) ∨ ( P ∧ R ) P \land (Q \lor R) \quad = \quad (P \land Q) \lor (P \land R) P ∧ ( Q ∨ R ) = ( P ∧ Q ) ∨ ( P ∧ R ) 分配律
P ∨ ( Q ∧ R ) = ( P ∨ Q ) ∧ ( P ∨ R ) P \lor (Q \land R) \quad = \quad (P \lor Q) \land (P \lor R) P ∨ ( Q ∧ R ) = ( P ∨ Q ) ∧ ( P ∨ R ) 分配律
¬ ( P ∧ Q ) = ¬ P ∨ ¬ Q \neg (P \land Q) \quad = \quad \neg P \lor \neg Q ¬ ( P ∧ Q ) = ¬ P ∨ ¬ Q 分配律
¬ ( P ∨ Q ) = ¬ P ∧ ¬ Q \neg (P \lor Q) \quad = \quad \neg P \land \neg Q ¬ ( P ∨ Q ) = ¬ P ∧ ¬ Q 分配律
谓词逻辑和 Event-B 里还可以写全称量词 存在量词
全称量词: Universal Quantification ∀ x . P 存在量词: Existential Quantification ∃ x . P \begin{aligned}
& \text{全称量词: Universal Quantification} \quad \forall x.P \\
& \text{存在量词: Existential Quantification} \quad \exist x.P \\
\end{aligned}
全称量词 : Universal Quantification ∀ x . P 存在量词 : Existential Quantification ∃ x . P
其中,P P P
写软件规范时,实际写出的全称和存在量化公式都是下面形式:
∀ x . ( x ∈ P ⇒ Q ) ∃ x . ( x ∈ P ∧ Q ) \begin{aligned}
& \forall x.(x \in P \Rightarrow Q) \\
& \exist x.(x \in P \land Q)
\end{aligned}
∀ x . ( x ∈ P ⇒ Q ) ∃ x . ( x ∈ P ∧ Q )
这两个公式说的是:对于属于类型 P P P x x x Q Q Q P P P x x x Q Q Q
一个集合 S S S
对于一个集合 S S S
e ∈ S e \in S e ∈ S e e e S S S e ∉ S e \notin S e ∈ / S S S S e e e
对于元素个数很少的集合,可以用枚举元素 SQUARES = { 1 , 4 , 9 , 16 , 25 } \text{SQUARES} = \{1,4,9,16,25\} SQUARES = { 1 , 4 , 9 , 1 6 , 2 5 }
集合的元素个数 c a r d ( S ) card(S) c a r d ( S ) c a r d ( { 2 , 4 , 6 } ) = 3 card(\{2,4,6\}) = 3 c a r d ( { 2 , 4 , 6 } ) = 3
空集 ∅ \varnothing ∅
如果要描述有很多元素的集合,可以采用集合的内涵(comprehension)表示方式 谓词 P P P
{ e ∣ e ∈ S ∧ P } \begin{Bmatrix}
e \mid e \in S \land P
\end{Bmatrix}
{ e ∣ e ∈ S ∧ P }
例如, SQUARES = { e ∣ n ∈ NAT 1 ∧ n ≤ 5 ∧ e = n × n } \text{SQUARES} = \{e \mid n\in \text{NAT}_1 \land n \le 5 \land e=n \times n\} SQUARES = { e ∣ n ∈ NAT 1 ∧ n ≤ 5 ∧ e = n × n }
下面我们给出一些基本集合:
数学表示
正文表示
说明
Z \mathbb{Z} Z INREGER整数集合,看作抽象集合
N \mathbb{N} N NATURAL自然数集合
I N T \mathbf{INT} I N T INT系统可实现的整数集合
N A T \mathbf{NAT} N A T NAT系统可实现的自然数集合
N A T 1 \mathbf{NAT}_1 N A T 1 NAT1N A T \mathbf{NAT} N A T
B O O L \mathbf{BOOL} B O O L BOOL布尔类型,只包括 TRUE 和 FALSE
其中,实际的整数只能是 I N T \mathbf{INT} I N T M I N I N T \mathbf{MININT} M I N I N T M A X I N T \mathbf{MAXINT} M A X I N T I N T \mathbf{INT} I N T
m . . n ≜ { i ∣ i ∈ Z ∧ m ≤ i ≤ n } m..n \triangleq \{i | i\in \mathbb{Z} \land m \le i \le n\}
m . . n ≜ { i ∣ i ∈ Z ∧ m ≤ i ≤ n }
例如, I N T = M I N I N T . . M A X I N T \mathbf{INT} = \mathbf{MININT} .. \mathbf{MAXINT} I N T = M I N I N T . . M A X I N T N A T = 0.. M A X I N T \mathbf{NAT} = 0..\mathbf{MAXINT} N A T = 0 . . M A X I N T
基本的集合运算是:
并集(Union):$S \cup T $
交集(Intersection):S ∩ T S \cap T S ∩ T
差集(Different):S − T S - T S − T
对于集合的集合
广义并集 ⋃ S S ≜ { e ∣ for all s ∈ S S ⋅ e ∈ s } \bigcup SS \triangleq \{e \mid \text{ for all } s \in SS · e \in s\} ⋃ S S ≜ { e ∣ for all s ∈ S S ⋅ e ∈ s } union SS广义交集 ⋂ S S ≜ { e ∣ for some s ∈ S S ⋅ e ∈ s } \bigcap SS \triangleq \{e \mid \text{ for some } s\in SS · e \in s\} ⋂ S S ≜ { e ∣ for some s ∈ S S ⋅ e ∈ s } inter SS
一个集合的幂集(PowerSet)是它的所有子集的集合:
幂集,所有子集 P S ≜ { T ∣ T ⊆ S } \mathbb{P}S \triangleq \{ T \mid T \subseteq S\} P S ≜ { T ∣ T ⊆ S } POW S
对于任何集合都有:
∅ ∈ P S \varnothing \in \mathbb{P}S ∅ ∈ P S S ∈ P S S \in \mathbb{P}S S ∈ P S
所有非空子集 P 1 S ≜ { T ∣ T ⊆ S ∧ T ≠ ∅ } \mathbb{P}_1S \triangleq \{ T \mid T \subseteq S \land T \ne \varnothing \} P 1 S ≜ { T ∣ T ⊆ S ∧ T = ∅ } POW1 S
两个集合 S S S T T T ( s , t ) (s,t) ( s , t ) S*T
S × T ≜ { ( s , t ) ∣ s ∈ S ∧ t ∈ T } S \times T \triangleq \{ (s,t) | s \in S \land t \in T\}
S × T ≜ { ( s , t ) ∣ s ∈ S ∧ t ∈ T }
集合之间的关系有:
数学表示
说明
注释
S = T S = T S = T S S S T T T S = T ≜ S ⊆ T ∧ T ⊆ S S = T\quad \triangleq \quad S \subseteq T \land T \subseteq S S = T ≜ S ⊆ T ∧ T ⊆ S
S ≠ T S \ne T S = T S S S
S ⊆ T S \subseteq T S ⊆ T S S S T T T S ⊆ T ≜ S ∈ P ( T ) S \subseteq T\quad \triangleq \quad S \in \mathbb{P}(T) S ⊆ T ≜ S ∈ P ( T )
S ⊂ T S \subset T S ⊂ T S S S T T T
S ⊈ T S \nsubseteq T S ⊈ T S S S T T T
S ⊄ T S \not\subset T S ⊂ T S S S T T T
显然,对于任何 S S S
S ⊆ S ∅ ⊆ S S \subseteq S \\
\varnothing \subseteq S
S ⊆ S ∅ ⊆ S
相关阅读:
Oneree 的博客:集合论与关系-有序对
我们集合的笛卡尔积部分介绍过,两个集合 S S S T T T S × T S \times T S × T 二元有序对 ( s , t ) (s,t) ( s , t ) s ∈ S s \in S s ∈ S s ↦ t s \mapsto t s ↦ t
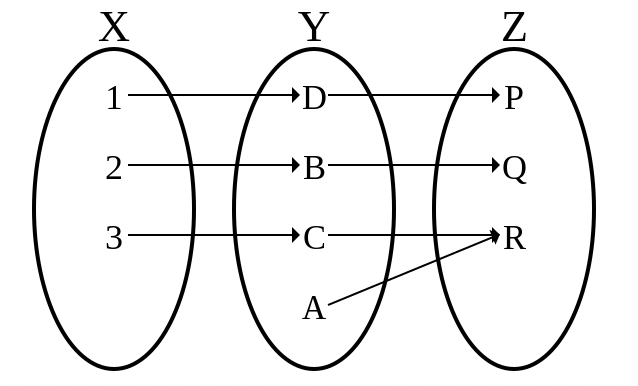
二元关系 S ↔ T S \leftrightarrow T S ↔ T
数学形式
解释
等价推理
S ↔ T S \leftrightarrow T S ↔ T 二元关系
r ∈ S ↔ T ≜ r ⊆ S × T r \in S \leftrightarrow T \quad \triangleq \quad r \subseteq S \times T r ∈ S ↔ T ≜ r ⊆ S × T
dom ( r ) \text{dom}(r) dom ( r ) 关系 r r r 定义域
E ∈ dom ( r ) ≜ ∃ y . ( E ↦ y ∈ r ) E \in \text{dom}(r) \quad \triangleq \quad \exist y.(E \mapsto y \in r) E ∈ dom ( r ) ≜ ∃ y . ( E ↦ y ∈ r )
ran ( r ) \text{ran}(r) ran ( r ) 关系 r r r 值域
E ∈ ran ( r ) ≜ ∃ x . ( x ↦ E ∈ r ) E \in \text{ran}(r) \quad \triangleq \quad \exist x.(x \mapsto E \in r) E ∈ ran ( r ) ≜ ∃ x . ( x ↦ E ∈ r )
r − 1 r^{-1} r − 1 关系 r r r 逆关系
E ↦ F ∈ r − 1 ≜ F ↦ E ∈ r 1 E \mapsto F \in r ^{-1} \quad \triangleq \quad F \mapsto E \in r ^{1} E ↦ F ∈ r − 1 ≜ F ↦ E ∈ r 1
部分满射(Partial Surjective)二元关系
if r ∈ S \text{if } r \in S if r ∈ S <->> T T T then ran ( r ) = T \text{ then ran}(r)=T then ran ( r ) = T
完全二元关系
if r ∈ S \text{if } r \in S if r ∈ S <<-> T T T then dom ( r ) = S \text{ then dom}(r)=S then dom ( r ) = S
全满射(Total Surjective)二元关系
if r ∈ S \text{if } r \in S if r ∈ S <<->> T T T then dom ( r ) = S ∧ ran ( r ) = T \text{ then dom}(r)=S \land \text{ran}(r)=T then dom ( r ) = S ∧ ran ( r ) = T
S ◃ r S \triangleleft r S ◃ r 限制关系 r r r S S S
S ◃ r S \triangleleft r S ◃ r ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ x ∈ S } \triangleq \quad \{x \mapsto y \mid x \mapsto y \in r \land x \in S\} ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ x ∈ S }
r ▹ T r \triangleright T r ▹ T 限制关系 r r r T T T
r ◃ T r \triangleleft T r ◃ T ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ y ∈ T } \triangleq \quad \{x \mapsto y \mid x \mapsto y \in r \land y \in T\} ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ y ∈ T }
限制关系 r r r 排除 S S S
≜ { x ↦ y ∣ x ↦ y ∈ r ∧ x ∉ S } \triangleq \quad \{x \mapsto y \mid x \mapsto y \in r \land x \notin S\} ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ x ∈ / S } ≜ ( dom ( r ) − S ) ◃ r \triangleq \quad (\text{dom}(r) - S) \triangleleft r ≜ ( dom ( r ) − S ) ◃ r
限制关系 r r r 排除 T T T
≜ { x ↦ y ∣ x ↦ y ∈ r ∧ y ∉ T } \triangleq \quad \{x \mapsto y \mid x \mapsto y \in r \land y \notin T\} ≜ { x ↦ y ∣ x ↦ y ∈ r ∧ y ∈ / T } ≜ r ▹ ( ran ( r ) − T ) \triangleq \quad r \triangleright (\text{ran}(r) - T) ≜ r ▹ ( ran ( r ) − T )
r [ S ] r[S] r [ S ] r [ S ] r[S] r [ S ] S S S r r r ≜ { y ∣ ∃ . x ∈ S ∧ x ↦ y ∈ r } \triangleq \quad \{y \mid \exist .x \in S \land x \mapsto y \in r\} ≜ { y ∣ ∃ . x ∈ S ∧ x ↦ y ∈ r } ≜ ran ( S ◃ r ) \triangleq \quad \text{ran}(S \triangleleft r) ≜ ran ( S ◃ r )
p ; q p;q p ; q 关系 p p p q q q
∀ p , q . p ∈ S ↔ T , q ∈ T ↔ U \forall p,q.\quad p \in S \leftrightarrow T,q \in T \leftrightarrow U ∀ p , q . p ∈ S ↔ T , q ∈ T ↔ U ≜ { x ↦ y ∣ ( ∃ z . x ↦ z ∈ p ∧ z ↦ y ∈ q ) } \triangleq \quad \{x\mapsto y \mid (\exist z. \; x \mapsto z \in p \land z \mapsto y \in q)\} ≜ { x ↦ y ∣ ( ∃ z . x ↦ z ∈ p ∧ z ↦ y ∈ q ) }
关系 p p p q q q
i d ( S ) id(S) i d ( S ) 集合 S S S
≜ { x ↦ y ∣ x ↦ y ∈ ( S × S ) ∧ x = y } \triangleq \quad \{x \mapsto y \mid x \mapsto y \in (S \times S) \land x=y\} ≜ { x ↦ y ∣ x ↦ y ∈ ( S × S ) ∧ x = y }
p ⊗ q p \otimes q p ⊗ q 关系 p p p q q q
≜ { x ↦ ( y ↦ z ) ∣ x ↦ y ∈ p ∧ y ↦ z ∈ q } \triangleq \quad \{x \mapsto (y \mapsto z) \mid x \mapsto y \in p \land y \mapsto z \in q\} ≜ { x ↦ ( y ↦ z ) ∣ x ↦ y ∈ p ∧ y ↦ z ∈ q }
p ∥ q p \parallel q p ∥ q 关系 p p p q q q
{ ( x ↦ y ) ↦ ( m ↦ n ) ∣ x , y , m , n . x ↦ m ∈ p ∧ y ↦ n ∈ q } \{(x \mapsto y) \mapsto (m \mapsto n) \mid x,y,m,n. \; x \mapsto m \in p \land y \mapsto n \in q\} { ( x ↦ y ) ↦ ( m ↦ n ) ∣ x , y , m , n . x ↦ m ∈ p ∧ y ↦ n ∈ q }
prj 1 ( r ) \text{prj}_1(r) prj 1 ( r ) 投影关系
≜ { x ∣ x ↦ y ∈ r } \triangleq \quad \{x \mid x \mapsto y \in r\} ≜ { x ∣ x ↦ y ∈ r }
prj 2 ( r ) \text{prj}_2(r) prj 2 ( r ) 投影关系
≜ { y ∣ x ↦ y ∈ r } \triangleq \quad \{y \mid x \mapsto y \in r\} ≜ { y ∣ x ↦ y ∈ r }
【示例】
p = { 1 ↦ 5 , 3 ↦ 9 , 6 ↦ 3 , 9 ↦ 2 } q = { 2 ↦ 7 , 3 ↦ 4 , 5 ↦ 1 , 9 ↦ 5 } S = { 1 , 2 , 3 } p [ S ] = { 5 , 9 } 关系p中以集合S为定义域的值的集合(像) p ; q = { 1 ↦ 1 , 3 ↦ 5 , 6 ↦ 4 , 9 ↦ 7 } \begin{aligned}
p \; & = \; \{ 1 \mapsto 5, 3 \mapsto 9, 6 \mapsto 3, 9 \mapsto 2\} \\
q \; & = \; \{ 2 \mapsto 7, 3 \mapsto 4, 5 \mapsto 1, 9 \mapsto 5\} \\
S \; & = \; \{1,2,3\} \\
p[S] & = \; \{5,9\} \quad \text{关系p中以集合S为定义域的值的集合(像)} \\
p;q & = \; \{1 \mapsto 1, 3 \mapsto 5, 6 \mapsto 4, 9 \mapsto 7\}
\end{aligned}
p q S p [ S ] p ; q = { 1 ↦ 5 , 3 ↦ 9 , 6 ↦ 3 , 9 ↦ 2 } = { 2 ↦ 7 , 3 ↦ 4 , 5 ↦ 1 , 9 ↦ 5 } = { 1 , 2 , 3 } = { 5 , 9 } 关系 p 中以集合 S 为定义域的值的集合(像) = { 1 ↦ 1 , 3 ↦ 5 , 6 ↦ 4 , 9 ↦ 7 }
函数是关系的特殊情况。对于关系,其定义域中的任意一个值都有若干个值与之对应。而对于函数 值域里最多只有一个对应的值
例如我们有一个函数关系 f f f
f = { 2 ↦ 5 , 3 ↦ 9 , 6 ↦ 3 , 9 ↦ 2 } f = \{ 2 \mapsto 5, 3 \mapsto 9, 6 \mapsto 3, 9 \mapsto 2 \}
f = { 2 ↦ 5 , 3 ↦ 9 , 6 ↦ 3 , 9 ↦ 2 }
该函数在定义域为 S = { 2 , 6 , 9 } S=\{2,6,9\} S = { 2 , 6 , 9 }
f [ S ] = f [ { 2 , 6 , 9 } ] = { 5 , 3 , 2 } f[S] = f[\{2,6,9\}] = \{5,3,2\}
f [ S ] = f [ { 2 , 6 , 9 } ] = { 5 , 3 , 2 }
对于任意一个函数 f f f a ↦ b ∈ f a \mapsto b \in f a ↦ b ∈ f
f ( a ) = b ,即 f [ { a } ] = { b } f(a)=b \text{,即 } f[\{a\}] = \{b\}
f ( a ) = b ,即 f [ { a } ] = { b }
【部分函数(Partial Function)】:
对于关系 r ∈ S ⇸ T r \in S ⇸ T r ∈ S ⇸ T a ∈ T a \in T a ∈ T ( r − 1 ; r ) ∈ i d ( T ) (r^{-1};r) \in id(T) ( r − 1 ; r ) ∈ i d ( T ) b ∈ r − 1 [ { a } ] b \in r^{-1} [\{a\}] b ∈ r − 1 [ { a } ] r [ { b } ] r[\{b\}] r [ { b } ] { a } \{a\} { a } r r r
f ∈ S ⇸ T ≜ f ∈ S ↔ T ∧ f − 1 ; f ⊆ i d ( ran ( f ) ) f \in S ⇸ T \quad \triangleq \quad f \in S \leftrightarrow T \land f^{-1};f \subseteq id(\text{ran}(f))
f ∈ S ⇸ T ≜ f ∈ S ↔ T ∧ f − 1 ; f ⊆ i d ( ran ( f ) )
【全函数(Total Function)】:
全函数是指,在部分函数的基础上使得关系 r r r dom ( r ) = S \text{dom}(r) = S dom ( r ) = S
f ∈ S → T ≜ f ∈ S ⇸ T ∧ S = dom ( f ) f \in S \to T \quad \triangleq \quad f \in S ⇸ T \land S = \text{dom}(f)
f ∈ S → T ≜ f ∈ S ⇸ T ∧ S = dom ( f )
数学形式
解释
等价推理
S ⇸ T S ⇸ T S ⇸ T 部分函数(Partial Function)
≜ f ⋅ f ∈ S ↔ T ∧ f − 1 ; f ⊆ i d ( ran ( f ) ) \triangleq \quad f \cdot f \in S \leftrightarrow T \land f^{-1};f \subseteq id(\text{ran}(f)) ≜ f ⋅ f ∈ S ↔ T ∧ f − 1 ; f ⊆ i d ( ran ( f ) )
S ↔ T S \leftrightarrow T S ↔ T 全函数(Total Function)
≜ f ⋅ f ∈ S ⇸ T ∧ S = dom ( f ) \triangleq \quad f \cdot f \in S ⇸ T \land S = \text{dom}(f) ≜ f ⋅ f ∈ S ⇸ T ∧ S = dom ( f )
部分单射(Partial Injection)
全单射(Total Injection)
部分满射(Partial Surjection)
全满射(Total Surjection)
全双射(Bijection)
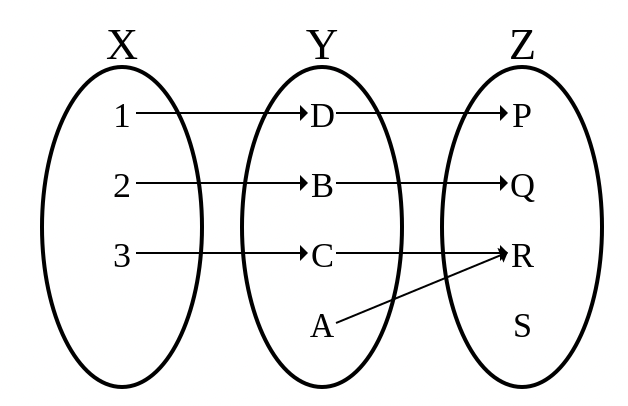
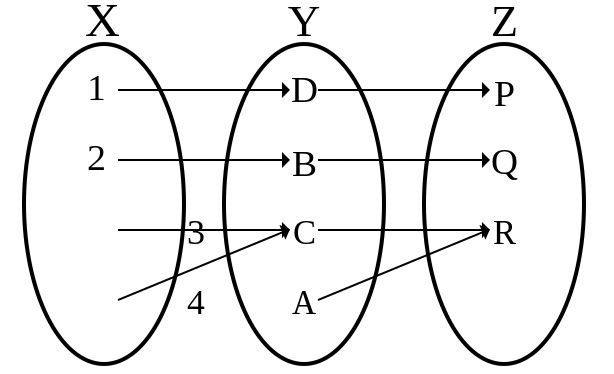
在数学定义中,单射 满射 双射 陪域 的关联方式所区分的三类映射 。
单射 单射 (一对一 )如果每个可能的像最多只有一个变量映射其上。等价的有,一个映射是单射如果它把不同值映射到不同像。一个单射映射简称单射 。下图中第二个映射不必是单射。
满射 满射 (到上)如果每个可能的像至少有一个变量映射其上,或者说陪域任何元素都有至少有一个变量与之对应。下图中第一个映射不必为满射。
双射 双射 。映射为双射当且仅当每个可能的像有且仅有一个变量与之对应。下图中第一个映射不必为满射、第二个映射不必为单射。
Event-BEvent-B 是一个基于事件 状态迁移(State- transition)模型系统 细化 证明
模型的定义是逐渐完善
首先设计一个初始的抽象自动机(Abstract Machine);
然后通过一系列的细化(Refinement)来完善这个初始的抽象机
一个模型包含了一个离散迁移系统的完整数学开发,它由分属两个类别的一些组件构成,这两个类别分别称为自动机 M a c h i n e Machine M a c h i n e 上下文 C o n t e x t Context C o n t e x t
自动机 M a c h i n e Machine M a c h i n e 动态部分
REFINES:定义该自动机是另一个抽象机的细化;SEES:用来引入一个上下文(C o n t e x t Context C o n t e x t VARIABLES:定义模型中的状态变量 INVARIANTS:定义了相应的变量 VARIABLES(状态)需要满足的状态(定义了相应 VARIABLES 的类型);THEOREMS:定义了相应的变量 VARIABLES(状态)需要满足的状态,和 SEES 的上下文中推导出的“约束”,(定义了相应 VARIABLES 的行为);VARIANT:相对于 VARIABLES 来说,是 EVENT 中临时变量 VARIABLES 小;EVENT:EVENT 则定义了能使状态变量改变的事件,其中包括初始化
上下文 C o n t e x t Context C o n t e x t 静态部分
EXTENDS:通过添加新的集合、常量、公理和定理来表达扩展(对另一个上下文的丰富);SETS:声明一些集合;CONSTANTS:定义的一些常量;AXIOMS:公理,定义集合和常量的属性,描述了不能从其他公理派生出来的属性;THEOREMS:描述了可以由 AXIOMS 公理
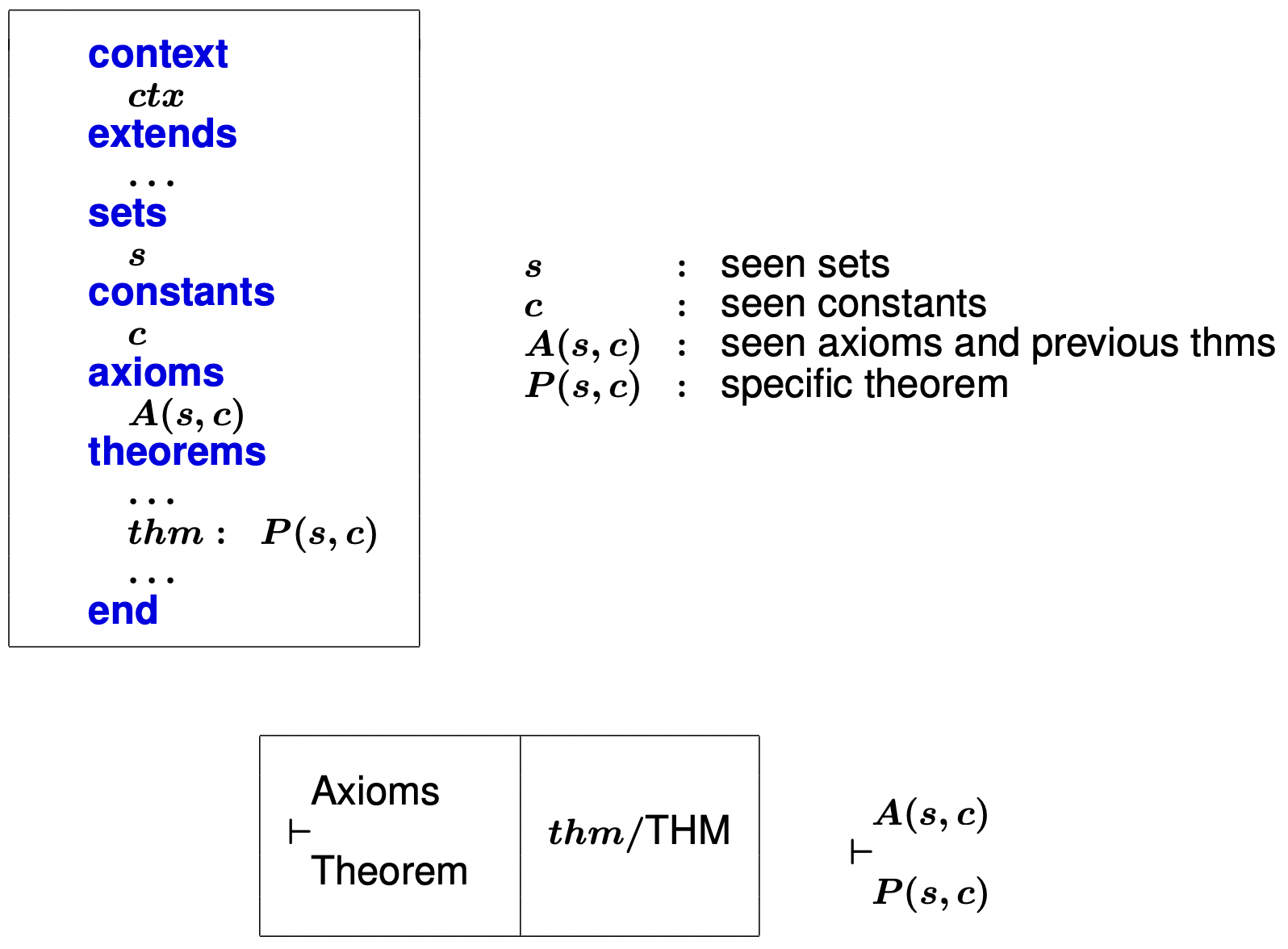
【C o n t e x t Context C o n t e x t
1 2 3 4 5 6 7 8 9 10 11 12 13 CONTEXT ctx EXTENDS actx // 上下文ctx扩展了另一个上下文actx, 并添加了一些新的元素 SETS s // 定义一个新集合s CONSTANTS c // 定义一个新常量c AXIOMS A_c : ... // 公理A_c定义了集合和常量的属性 THEOREMS T_c : ... // 定义了从公理和定理推导出的一些定理 END
【M a c h i n e Machine M a c h i n e
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 MACHINE m // 自动机m对应的系统模型 REFINES am // 自动机m从抽象机am细化而来 SEES acts // 将上下文acts导入抽象机m VARIABLES x // 自动机的变量(状态) INVARIANTS inv(x) // 关于变量x的不变量"约束" THEOREMS t(x) // 从上下文推导出的定义和不变量"约束" VARIANT v // EVENTS ev1: ... // ev1, ... 描述状态变化的机器事件列表,至少有一个 INITIALISATION 事件 ... END
在抽象机中,VARIABLES 的修改
Before-After Predicates(BAP)
解释
S k i p Skip S k i p NULL / 为空的动作
x : = E x := E x : = E 为 x x x E E E
x : ∈ S x :\in S x : ∈ S 使 x x x S S S
x : ∣ P x : \mid P x : ∣ P 使 x x x P P P
f ( x ) : = E f(x):=E f ( x ) : = E
可以使用 x : ∣ P x : \mid P x : ∣ P P ( x , x ′ ) P(x,x') P ( x , x ′ )
x 1 , . . . , x n : ∣ P x_1,...,x_n : \mid P
x 1 , . . . , x n : ∣ P
【初始化】定义状态变量的初始化的值。
【状态变量的修改】Before-After Predicates,BAP(x,x')。例如 x : ∣ ( x ′ = x + 1 ) or x : = x + 1 x : \mid (x'=x+1) \text{ or } x := x+1 x : ∣ ( x ′ = x + 1 ) or x : = x + 1
【三种类型的事件】:
无卫(Non guarded)事件:P ( x , x ′ ) P(x,x') P ( x , x ′ ) g r d ( E ) grd(E) g r d ( E ) TRUE \text{TRUE} TRUE
1 2 3 4 event_non_guarded = BEGIN x :| BAP(x, x') END
有卫(Guarded)事件:G ( x ) ∧ P ( x , x ′ ) G(x) \land P(x,x') G ( x ) ∧ P ( x , x ′ ) g r d ( E ) grd(E) g r d ( E ) G ( x ) G(x) G ( x )
1 2 3 4 5 6 event_guarded = WHEN G(x) BEGIN x :| BAP(x, x') END
有参(Parameterised)事件:∃ I . ( G ( x , I ) ∧ P ( x , x ′ , I ) ) \exist I.(G(x, I) \land P(x,x',I)) ∃ I . ( G ( x , I ) ∧ P ( x , x ′ , I ) ) g r d ( E ) grd(E) g r d ( E ) ∃ I . G ( x , I ) \exist I.G(x, I) ∃ I . G ( x , I )
1 2 3 4 5 6 7 8 event_guarded = ANY I WHERE G(x,I) BEGIN x :| BAP(x, x', I) END
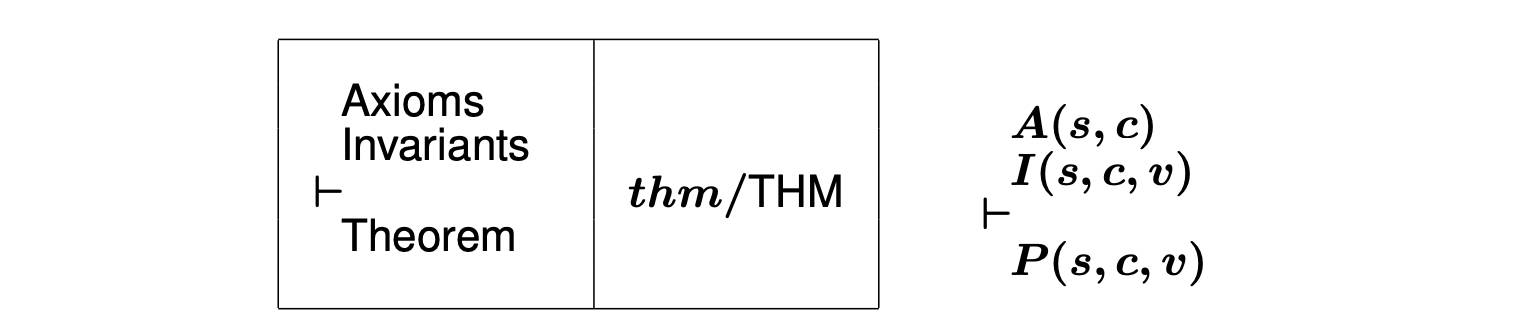
其关于细化的证明义务(PO)规则为:
(Γ ( s , c ) \Gamma(s,c) Γ ( s , c ) s , c s,c s , c s , c s,c s , c A x i o m Axiom A x i o m 本章最后的部分:义务证明 中查看更详细的内容)
POs
数学表达
Invariant preservation at initialisationINIT
Γ ( s , c ) ⊢ I n i t ( x ) \Gamma(s,c) \vdash Init(x) Γ ( s , c ) ⊢ I n i t ( x ) ⇒ I ( x ) \Rightarrow I(x) ⇒ I ( x )
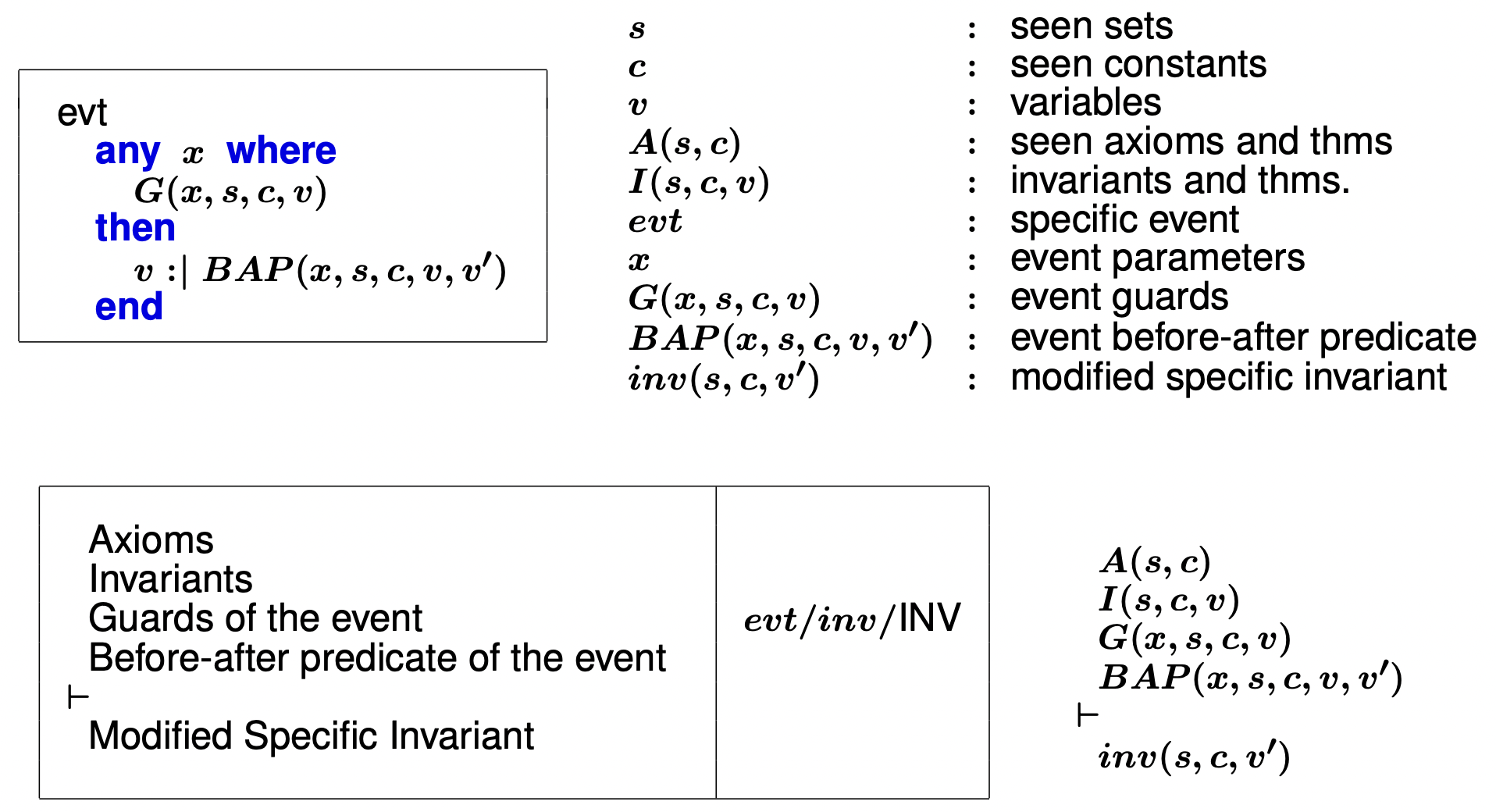
Invariant preservation by each eventINV
Γ ( s , c ) ⊢ I ( x ) ∧ G ( I , x ) ∧ B A P ( x , x ′ , l ) \Gamma(s,c) \vdash I(x) \land G(I,x) \land BAP(x,x',l) Γ ( s , c ) ⊢ I ( x ) ∧ G ( I , x ) ∧ B A P ( x , x ′ , l ) ⇒ I ( x ′ ) \Rightarrow I(x') ⇒ I ( x ′ )
Deadlock freenessDEAD
Γ ( s , c ) ⊢ I ( x ) \Gamma(s,c) \vdash I(x) Γ ( s , c ) ⊢ I ( x ) ( g r d ( e 1 ) ∨ . . . ∨ g r d ( e n ) ) (grd(e_1) \lor ... \lor grd(e_n)) ( g r d ( e 1 ) ∨ . . . ∨ g r d ( e n ) )
Theorems shall be proveSAFE
Γ ( s , c ) ⊢ I ( x ) \Gamma(s,c) \vdash I(x) Γ ( s , c ) ⊢ I ( x ) T h e o r e m ( x ) T_{heorem}(x) T h e o r e m ( x )
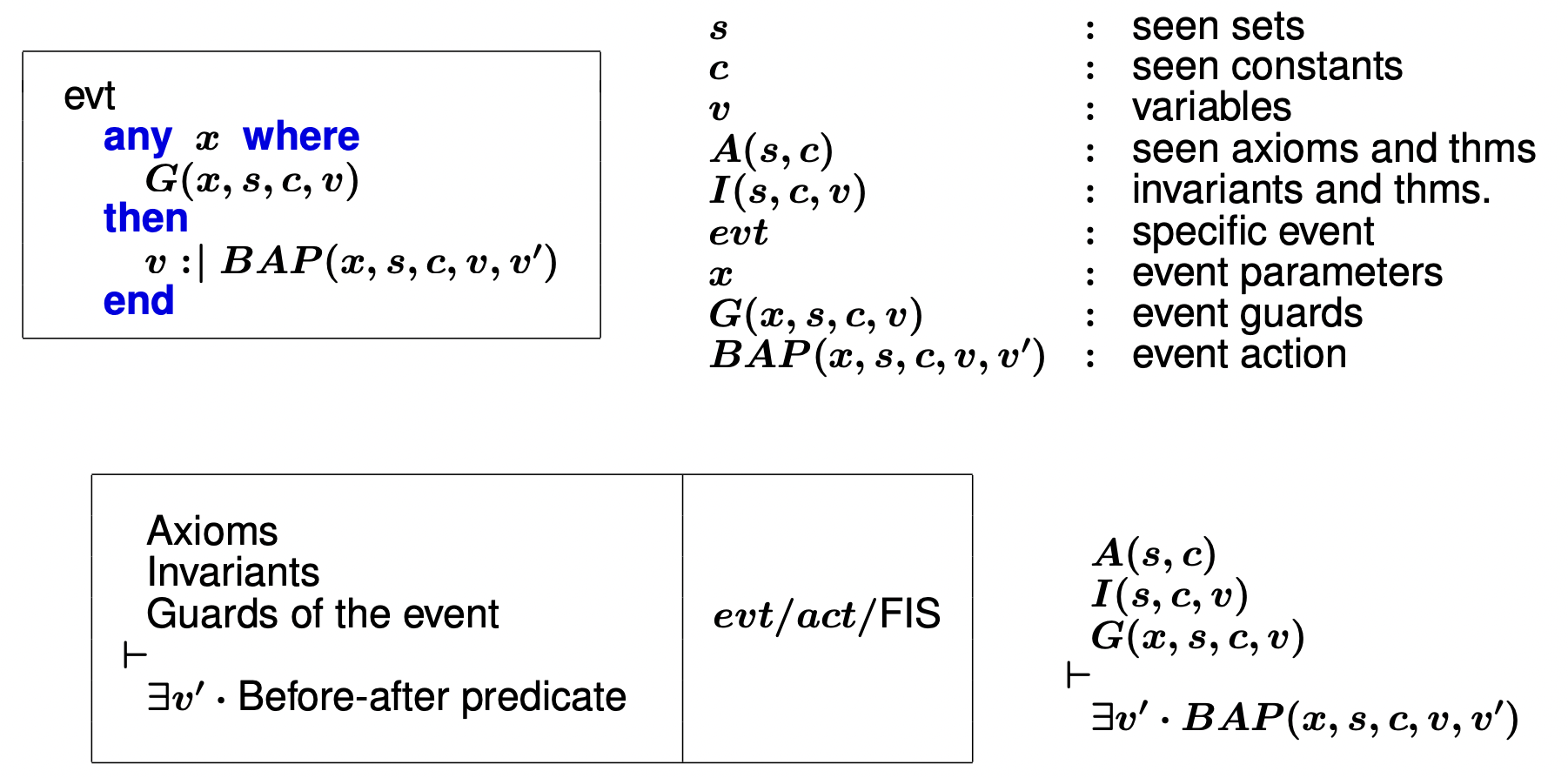
Events shall be feasibleFIS
Γ ( s , c ) ⊢ I ( x ) ∧ G ( I , x ) \Gamma(s,c) \vdash I(x) \land G(I,x) Γ ( s , c ) ⊢ I ( x ) ∧ G ( I , x ) ⇒ ∃ x ′ . B A P ( x , x ′ , l ) \Rightarrow \exist x'.BAP(x,x',l) ⇒ ∃ x ′ . B A P ( x , x ′ , l )
一个项目中可以存在多个 M a c h i n e Machine M a c h i n e C o n t e x t Context C o n t e x t
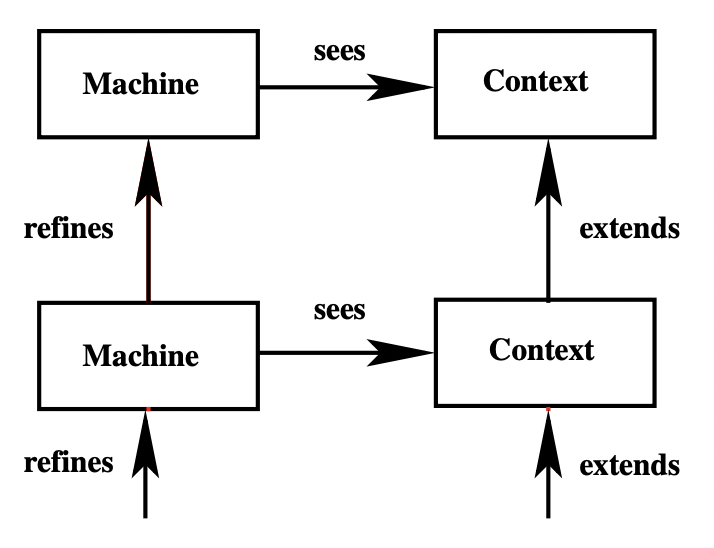
抽象机和上下文之间存在多种关系:一个抽象机可以被另一个抽象机“细化”(refines),一个上下文可以被另一个上下文“扩展”(extends),一个抽象机可以“观看”一个或几个上下文,下图描绘了机器和上下文之间的关系:
"Machines and contexts have various relationships: a machine can be ”refined” by another one, and a context can be ”extended” by another one (no cycles are allowed in both these relationships).
Moreover, a machine can ”see” one or several contexts. An example of machine and context relationship is as follows:"
细化是增加系统的功能、增加细节、改变状态模型。细化一个自动机过程中,可能需要增加新的变量和新的事件。一般一个模型需要进行多次细化才能符合要求。即 Machine 在细化中越来越复杂,越来越细致。C o n t e x t Context C o n t e x t M a c h i n e Machine M a c h i n e C o n t e x t Context C o n t e x t
一个 M a c h i n e Machine M a c h i n e SEES(导入)若干上下文(也可以不引入上下文)。
一个 C o n t e x t Context C o n t e x t EXTENDS(扩充)若干上下文(也可以不扩充任何上下文)。
上下文扩充的概念具有传递性 C 2 C_2 C 2 C 1 C_1 C 1 C 1 C_1 C 1
当上下文 C 2 C_2 C 2 C 1 C_1 C 1 C 1 C_1 C 1 C 2 C_2 C 2
把细化和扩充关系放一起,不允许出现任何循环
一个 M a c h i n e Machine M a c h i n e
一个 M a c h i n e Machine M a c h i n e SEES(导入)的上下文必须不小于它所细化的那一个抽象机。
抽象(Abstract)模型使用变量 x x x y y y
对于抽象机:INVARIANTS 为 I ( x ) I(x) I ( x )
对于细化的 M a c h i n e Machine M a c h i n e INVARIANTS 为 J ( x , y ) J(x,y) J ( x , y )
M a c h i n e Machine M a c h i n e J ( x , y ) J(x,y) J ( x , y ) M a c h i n e Machine M a c h i n e M a c h i n e Machine M a c h i n e
抽象机之间的细化关系是指对应事件之间具有细化关系,事件之间的细化关系是指对应事件的卫式条件满足卫式条件加强、动作满足模拟关系。
graph LR
MACHINE之间的细化 --"是指"--> EVENT之间的细化
EVENT之间的细化 --"是指"--> GUARD条件加强,动作满足模拟关系
对于事件:
一个新事件 Skip 事件
对于一个具体(Concrete)的事件:通过与其对应的抽象(Abstract)事件细化得来。
注意
我们假设一个抽象事件中有变量(variable) x x x y y y
抽象事件中的不定式(Invariant)为 I ( x ) I(x) I ( x ) J ( x , y ) J(x,y) J ( x , y ) 抽象和其本身参数的不定式
对于一个如下所示的新事件 Skip 事件
其中,细化的具体事件的不定式义务证明
(其他条件,如AXIOMS等) ∧ I ( x ) ∧ J ( x , y ) ∧ H ( y ) ⇒ J ( x , F ( y ) ) \begin{aligned}
& \text{(其他条件,如AXIOMS等)} \\
\land \quad & I(x) \land J(x,y) \land H(y) \\
\Rightarrow \quad & J(x,F(y))
\end{aligned}
∧ ⇒ ( 其他条件,如 AXIOMS 等 ) I ( x ) ∧ J ( x , y ) ∧ H ( y ) J ( x , F ( y ) )
对于一个如下所示的有卫事件
其中,细化的具体事件的不定式义务证明
(其他条件,如AXIOMS等) ∧ I ( x ) ∧ J ( x , y ) ∧ H ( y ) ⇒ G ( x ) ∧ J ( E ( x ) , F ( y ) ) \begin{aligned}
& \text{(其他条件,如AXIOMS等)} \\
\land \quad & I(x) \land J(x,y) \land H(y) \\
\Rightarrow \quad & G(x) \land J(E(x),F(y))
\end{aligned}
∧ ⇒ ( 其他条件,如 AXIOMS 等 ) I ( x ) ∧ J ( x , y ) ∧ H ( y ) G ( x ) ∧ J ( E ( x ) , F ( y ) )
对于一个如下所示的含参有卫事件
其中,细化的具体事件的不定式义务证明
(其他条件,如AXIOMS等) ∧ I ( x ) ∧ J ( x , y ) ∧ H ( y , w ) ⇒ ∃ v . ( G ( x , v ) ∧ J ( E ( x , v ) , F ( y , v ) ) ) \begin{aligned}
& \text{(其他条件,如AXIOMS等)} \\
\land \quad & I(x) \land J(x,y) \land H(y,w) \\
\Rightarrow \quad & \exist v. (G(x,v) \land J(E(x,v),F(y,v)))
\end{aligned}
∧ ⇒ ( 其他条件,如 AXIOMS 等 ) I ( x ) ∧ J ( x , y ) ∧ H ( y , w ) ∃ v . ( G ( x , v ) ∧ J ( E ( x , v ) , F ( y , v ) ) )
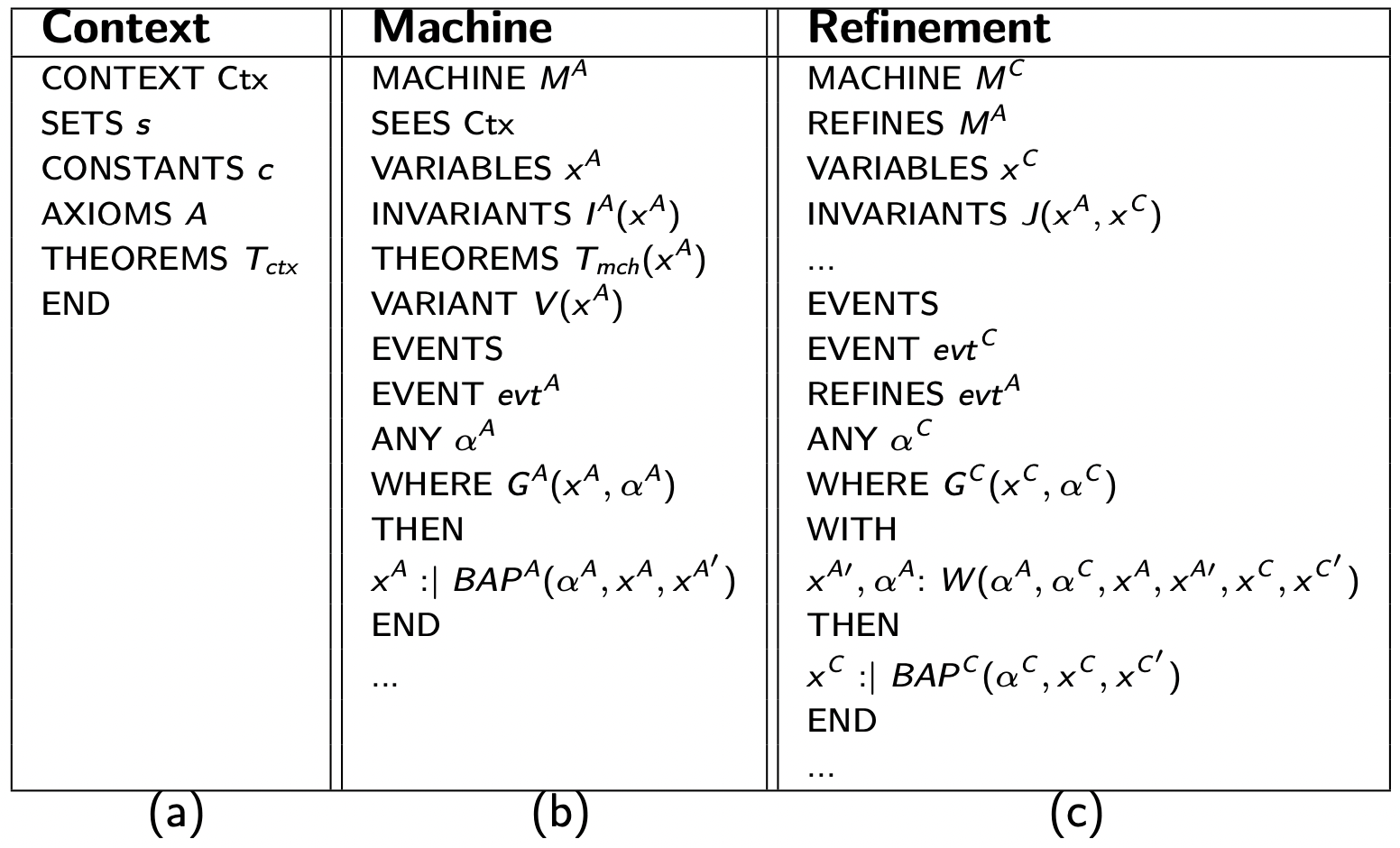
此时,我们考虑一个任意的抽象机及其对应的具体机:
其关于细化的义务推理(PO)规则为:
POs
数学表示
(6 INIT
A ∧ G C ( α C ) ∧ W ( α A , α C , x A ′ , x C ′ ) ∧ B A P C ( α C , x C ′ ) A \land G^C(\alpha ^C) \land W(\alpha ^A, \alpha ^C, x^{A\prime}, x^{C\prime}) \land BAP^C(\alpha^C, x^{C\prime}) A ∧ G C ( α C ) ∧ W ( α A , α C , x A ′ , x C ′ ) ∧ B A P C ( α C , x C ′ ) ⇒ J ( x A ′ , x C ′ ) \Rightarrow J(x^{A\prime}, x^{C\prime}) ⇒ J ( x A ′ , x C ′ )
Invariant preservationINV
A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ B A P C ( x C , α C , x C ′ ) A \land G^C(x^C, \alpha ^C) \land W(\alpha ^A, \alpha ^C, x^A, x^{A\prime}, x^C, x^{C\prime}) \land BAP^C(x^C, \alpha^C, x^{C\prime}) A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ B A P C ( x C , α C , x C ′ ) ∧ I A ( x A ) ∧ J ( x A , x C ) \land I^A(x^A) \land J(x^A, x^C) ∧ I A ( x A ) ∧ J ( x A , x C ) ⇒ J ( x A ′ , x C ′ ) \Rightarrow J(x^{A\prime}, x^{C\prime}) ⇒ J ( x A ′ , x C ′ )
Event SimulationSIM
A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ B A P C ( x C , α C , x C ′ ) A \land G^C(x^C, \alpha ^C) \land W(\alpha ^A, \alpha ^C, x^A, x^{A\prime}, x^C, x^{C\prime}) \land BAP^C(x^C, \alpha^C, x^{C\prime}) A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ B A P C ( x C , α C , x C ′ ) ∧ I A ( x A ) ∧ J ( x A , x C ) \land I^A(x^A) \land J(x^A, x^C) ∧ I A ( x A ) ∧ J ( x A , x C ) ⇒ B A P A ( x A , α A , x A ′ ) \Rightarrow BAP^A(x^A, \alpha ^A, x^{A\prime}) ⇒ B A P A ( x A , α A , x A ′ )
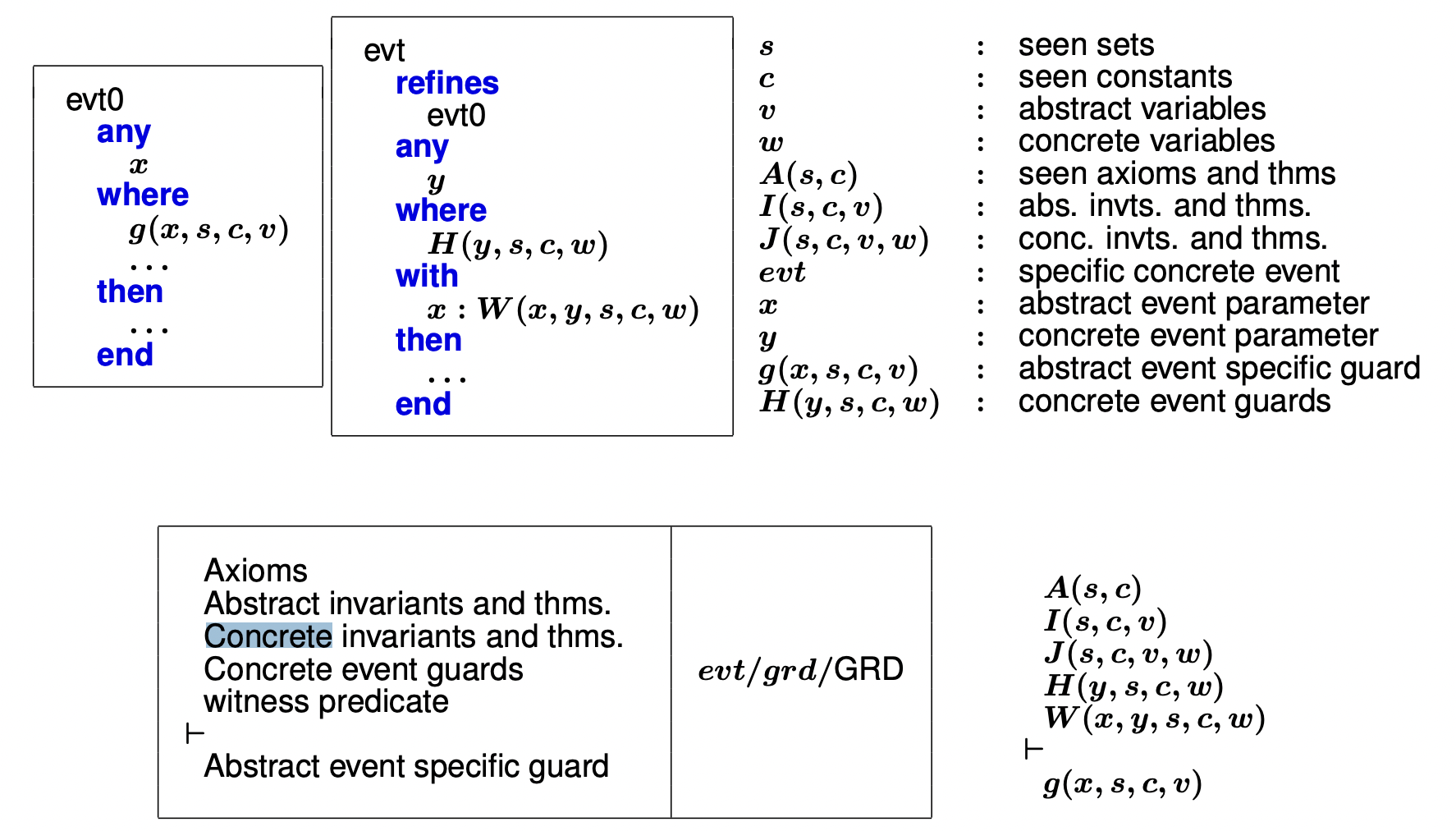
Guard StrengtheningGS
A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ I A ( x A ) ∧ J ( x A , x C ) A \land G^C(x^C, \alpha ^C) \land W(\alpha ^A, \alpha ^C, x^A, x^{A\prime}, x^C, x^{C\prime}) \land I^A(x^A) \land J(x^A, x^C) A ∧ G C ( x C , α C ) ∧ W ( α A , α C , x A , x A ′ , x C , x C ′ ) ∧ I A ( x A ) ∧ J ( x A , x C ) ⇒ G A ( x A , α A ) \Rightarrow G^A(x^A, \alpha^A) ⇒ G A ( x A , α A )
证明义务规则定义定义了“对一个 Event-B 模型必须证明些什么”。证明义务(proof obligation)并不是为了得到某些信息而进行的操作,它并不是必须的。它的作用只是确定建立的模型是否符合原始需求以及内部需求。
Rodin 平台中有一个称为证明义务生成器的工具,它对上下文和抽象机的正文做一些静态检查,自动确定要证明的东西。这些相继式被送给证明器,在那里完成自动的或者交互式的证明。证明义务规则包括:
不变式保持证明义务规则(Invariant Preservation):这一证明义务规则保证机器里的每一条不变式被每个事件保持
“Ensuring that each invariant is preserved by each event.”
可行性证明义务规则(Feasibility PO):这一证明义务规则的用途是保证非确定性动作的可行性。
“Ensuring that each non-deterministic action is feasible.”
卫加强证明义务规则:这一证明义务规则的用途是保证一个具体事件的具体卫强于
“Ensuring that each abstract guard is stronger than the concrete ones in the refining event. This ensures that when a concrete event is enabled then so is the corresponding abstract one.”
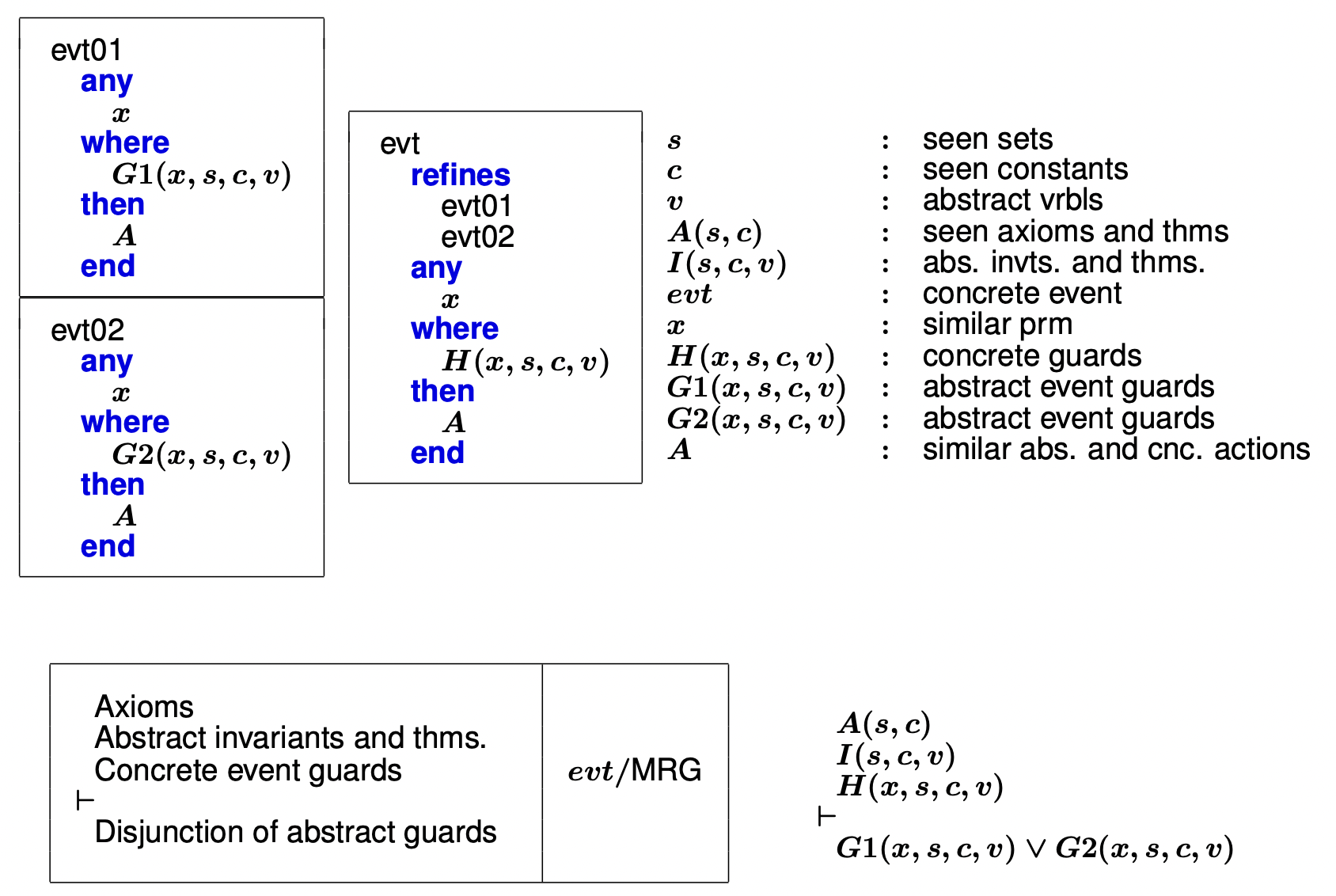
归并证明义务规则:这一证明义务保证,当一个具体事件归并了两个抽象事件时,它的卫应强于那两个抽象事件卫的析取。
模拟证明义务规则:这一证明义务规则的作用是保证在一个具体事件每一个抽象事件的每个动作,在相应的具体事件里都得到了正确的模拟。
“Ensuring that each action in a concrete event simulates the corresponding abstract action.”
数值变动式证明义务规则:这一证明义务规则保证,在每个收敛的或者预期事件的卫条件下,我们提出的变动式确实是有自然数值。
“Ensuring that under the guards of each convergent event a proposed numeric variant is indeed a natural number.”
有穷集变动式证明义务规则:这一证明义务规则保证,在每个收敛的或者预期事件的卫条件下,我们提出的集合变动式确实是一个有穷集。
“Ensuring that a proposed set variant is indeed a finite set.”
变动量证明义务规则:这一证明义务规则保证,每一个收敛事件都能使我们提出的数值变动式或者有穷集变动式减小。它也保证了每一个预期事件不会增大我们提出的数值变动式或有穷集变动式。
“Ensuring that each convergent event decreases the proposed numeric variant.”
非确定性见证证明义务规则:这一证明义务规则保证,在一个具体事件的见证谓词中提出的每个见证都存在。
“Ensuring that each witness proposed in the witness predicate of a concrete event indeed exists.”
定理证明义务规则:这一证明义务规则保证所提出的上下文或及其定理是可证的。定理的重要性在于有可能简化证明。
“Ensuring that a proposed context theorem is indeed provable.”
良好证明义务规则:这一证明义务规则保证,每个有可能病态定义的公理、定理、不变式、卫、动作、变动式或者见证都确实是良好定义的。
“Ensuring that a potentially ill-defined axiom, theorem, invariant, guard, action, variant, or witness is indeed well-defined.”