写在前面:
本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T. ) 第九学期课程 “Real Time System Scheduling” 及以下参考资料总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
与我们日常使用的操作系统不同,实时系统不仅要求计算结果正确,而且要求结果必须在一个特定的截止期限内产生 时间约束
例如我们在实验中遇到的自平衡车 传感器反馈的数据 实时地 一段时间内不会倾倒 时间约束
“A real-time system is able, first to read all incoming data before they become useless, second to give an appropriate timely reaction.”
“一个实时系统首先能够在所有传入的数据变得无用之前读取它们,其次能够及时做出适当的反应”
由此可见,实时系统的一个最大的特点就是时间正确性
然而在时间的约束上也有严格与不严格之分:
在实时系统中,一个应用通常由一组任务构成,每个任务完成应用中的一部分功能,组合后为用户提供特定的服务。根据任务的周期划分实时任务,可以分为 3 类:
我们通常规定,在处理器的时序图中,
使用向上的箭头 ↑ \uparrow ↑ 一个周期的开始时间 就绪时间
使用向下的箭头 ↓ \downarrow ↓ 截止时间 deadline
周期任务 按一定周期达到并请求运行 P P P C C C D D D 0 ≤ C ≤ D ≤ P 0 \le C \le D \le P 0 ≤ C ≤ D ≤ P
偶发任务 时间间隔一定 ≥ \ge ≥
非周期性任务 最迟开始时间 最迟结束时间
我们也可以对任务赋予有优先级
在抢占式
在非抢占式
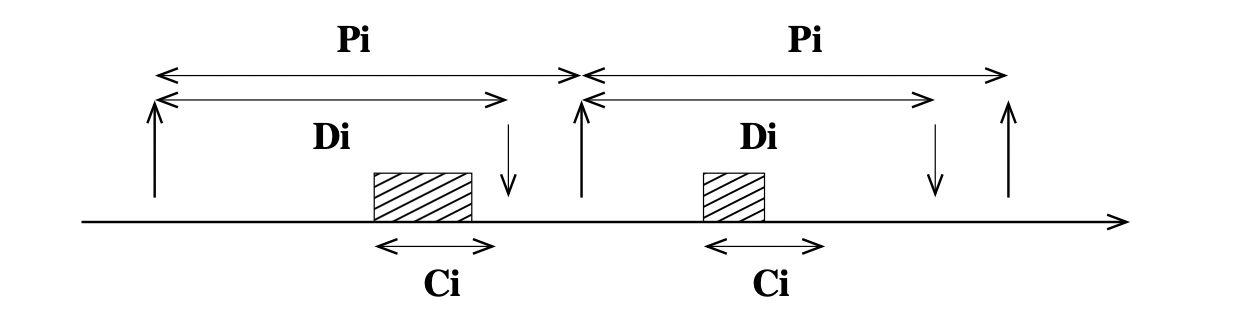
一个任务 T i T_i T i T i T_i T i
最坏情况下的执行时间 WCET W orst-C ase E xecution T ime):
执行一项工作所花费时间的安全上限,即实际执行时间(下图中用阴影表示)应该小于等于这个上限。使用 C i C_i C i
“Safe upper bound on the execution time of one job of the task”
(对于一个周期性任务)周期
在该任务中,连续的两个工作间的持续时间。使用 P i P_i P i
提示
周期 P i P_i P i 两个向上的箭头 ↑ \uparrow ↑
“(Minimum) duration between consecutive job releases of the task”
相对的截止时间
任务中每项工作的最大允许响应时间。使用 D i D_i D i
表现在图上就是向上的箭头 ↑ \uparrow ↑ ↓ \downarrow ↓
“Maximum allowed response time for each job of the task”
当我们在一个多任务(multitask)的系统内编排这些任务时,就需要引入调度器(Scheduler)与不同的调度策略(Scheduling strategy)。
在多任务的实时系统中,任务必须满足实时约束
“The worst-case response time of every job of every task is not greater than the task’s relative deadline”
"任务中每项工作 T i T_i T i C i C_i C i WCET D i D_i D i
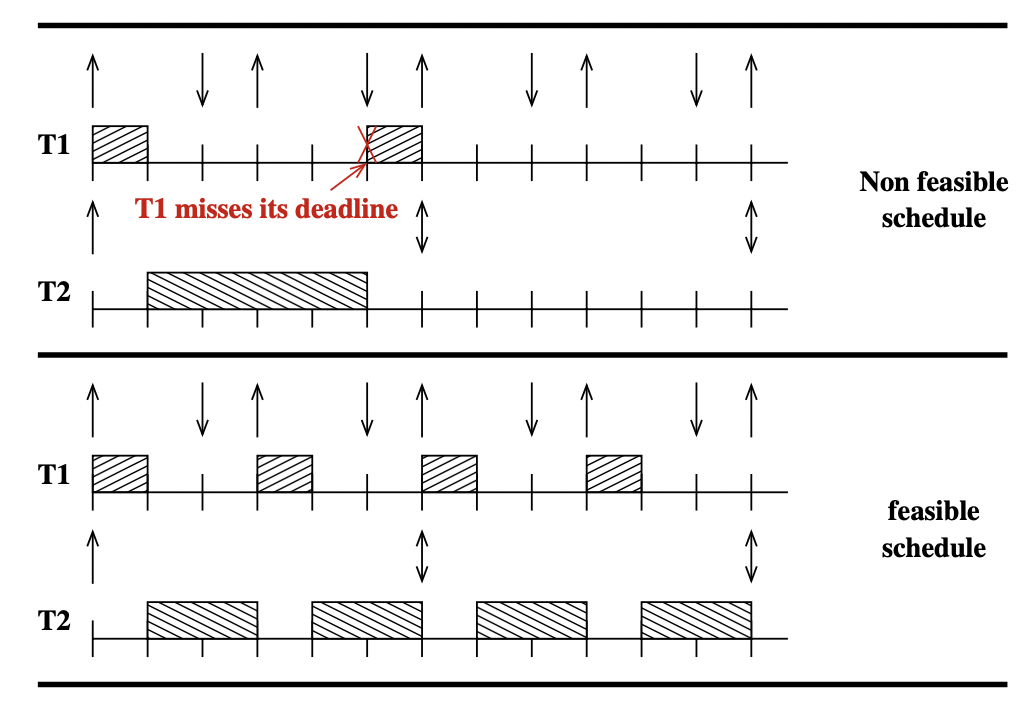
如下图,我们给出任务 T 1 T_1 T 1 T 2 T_2 T 2
T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 3 ) T_1 (r_1:0, \; C_1:1, \; D_1:2, \; P_1:3) T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 3 ) T 2 ( r 2 : 0 , C 2 : 4 , D 2 : 6 , P 2 : 6 ) T_2 (r_2:0, \; C_2:4, \; D_2:6, \; P_2:6) T 2 ( r 2 : 0 , C 2 : 4 , D 2 : 6 , P 2 : 6 )
我们可以看到,第一种调度显然是一种非抢占式 T 2 T_2 T 2 T 1 T_1 T 1 T 2 T_2 T 2 T 1 T_1 T 1 D 2 D_2 D 2 T 1 T_1 T 1 T 1 T_1 T 1
第二种调度显然是一种抢占式
我们假设若干个任务 T n T_n T n
Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 ) > . . . > Priority ( T n ) \text{Priority}(T_1) > \text{Priority}(T_2) > \text{Priority}(T_3) > ... >\text{Priority}(T_n)
Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 ) > . . . > Priority ( T n )
我们做出如下定义:
下面,我们将给出一个关于任务 T 1 T_1 T 1 T 2 T_2 T 2
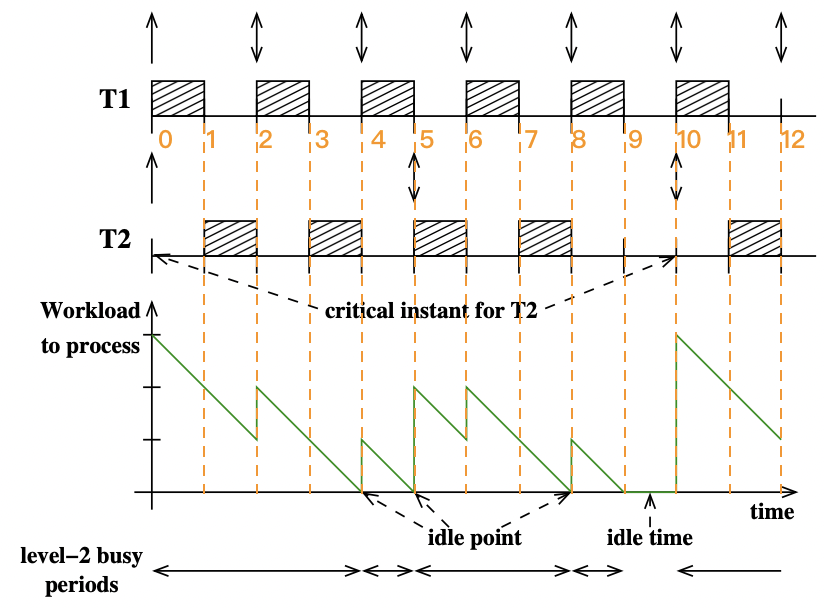
T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 2 ) T_1 (r_1:0, \; C_1:1, \; D_1:2, \; P_1:2) T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 2 ) T 2 ( r 2 : 0 , C 2 : 2 , D 2 : 5 , P 2 : 5 ) T_2 (r_2:0, \; C_2:2, \; D_2:5, \; P_2:5) T 2 ( r 2 : 0 , C 2 : 2 , D 2 : 5 , P 2 : 5 ) Priority ( T 1 ) > Priority ( T 2 ) \text{Priority}(T_1) > \text{Priority}(T_2) Priority ( T 1 ) > Priority ( T 2 ) CPU 空闲点(idle point)
【逐步分析】:
在分析之前,我们观察到各个任务周期的最小公倍数 L C M 1 ≤ i ≤ n LCM_{1\le i \le n} L C M 1 ≤ i ≤ n
L C M 1 ≤ i ≤ n ( P 1 , P 2 , . . . P n ) , 关 于 所 有 周 期 P i 的 最 大 公 约 数 LCM_{1\le i \le n}(P_1,P_2,...P_n), 关于所有周期P_i的最大公约数
L C M 1 ≤ i ≤ n ( P 1 , P 2 , . . . P n ) , 关 于 所 有 周 期 P i 的 最 大 公 约 数
第 0 时刻,任务 T 1 T_1 T 1 T 2 T_2 T 2 竞争时刻 T 1 T_1 T 1 Level-2 繁忙阶段 C 1 : 0 / 1 C_1:0/1 C 1 : 0 / 1 C 2 : 0 / 2 C_2:0/2 C 2 : 0 / 2
第 1 时刻,任务 T 1 T_1 T 1 执行完毕 T 2 T_2 T 2 处于就绪时刻 T 2 T_2 T 2 Level-2 繁忙阶段 C 1 : 1 / 1 C_1:1/1 C 1 : 1 / 1 C 2 : 0 / 2 C_2:0/2 C 2 : 0 / 2
第 2 时刻,任务 T 1 T_1 T 1 新周期的就绪时刻 T 2 T_2 T 2 处理了一个单位时间 T 1 T_1 T 1 所以暂停 T 2 T_2 T 2 T 1 T_1 T 1 Level-2 繁忙阶段 C 1 : 0 / 1 C_1:0/1 C 1 : 0 / 1 C 2 : 1 / 2 C_2:1/2 C 2 : 1 / 2
第 3 时刻,任务 T 1 T_1 T 1 执行完毕 T 2 T_2 T 2 继续执行 T 2 T_2 T 2 Level-2 繁忙阶段 C 1 : 1 / 1 C_1:1/1 C 1 : 1 / 1 C 2 : 1 / 2 C_2:1/2 C 2 : 1 / 2
第 4 时刻,任务 T 1 T_1 T 1 新周期的就绪时刻 T 2 T_2 T 2 执行完毕 所以开始执行 T 1 T_1 T 1 Level-2 繁忙阶段 C 1 : 0 / 1 C_1:0/1 C 1 : 0 / 1 C 2 : 2 / 2 C_2:2/2 C 2 : 2 / 2
第 5 时刻,任务 T 1 T_1 T 1 执行完毕 T 2 T_2 T 2 新周期的就绪时刻 T 2 T_2 T 2 Level-2 繁忙阶段 C 1 : 1 / 1 C_1:1/1 C 1 : 1 / 1 C 2 : 0 / 2 C_2:0/2 C 2 : 0 / 2
第 6 时刻,任务 T 1 T_1 T 1 新周期的就绪时刻 T 2 T_2 T 2 处理了一个单位时间 T 1 T_1 T 1 所以暂停 T 2 T_2 T 2 T 1 T_1 T 1 Level-2 繁忙阶段 C 1 : 0 / 1 C_1:0/1 C 1 : 0 / 1 C 2 : 1 / 2 C_2:1/2 C 2 : 1 / 2
第 7 时刻,任务 T 1 T_1 T 1 执行完毕 T 2 T_2 T 2 继续执行 T 2 T_2 T 2 Level-2 繁忙阶段 C 1 : 1 / 1 C_1:1/1 C 1 : 1 / 1 C 2 : 1 / 2 C_2:1/2 C 2 : 1 / 2
第 8 时刻,任务 T 1 T_1 T 1 新周期的就绪时刻 T 2 T_2 T 2 执行完毕 所以开始执行 T 1 T_1 T 1 Level-2 繁忙阶段 C 1 : 0 / 1 C_1:0/1 C 1 : 0 / 1 C 2 : 2 / 2 C_2:2/2 C 2 : 2 / 2
第 9 时刻,任务 T 1 T_1 T 1 执行完毕 T 2 T_2 T 2 执行完毕 所以没有任务执行 Level-2 繁忙阶段 C 1 : 1 / 1 C_1:1/1 C 1 : 1 / 1 C 2 : 2 / 2 C_2:2/2 C 2 : 2 / 2
第 10 时刻与第 0 时刻完全相同,因为两个任务周期(P 1 : 2 P_1:2 P 1 : 2 P 2 : 5 P_2:5 P 2 : 5 LCM
在上面的例子中,我们发现在第 9 时刻到第 10 时刻内 空闲
我们使用 U U U
U = ∑ i = 1 n C i P i ≤ 1 U = \sum ^{n} _{i=1} \frac {C_i} {P_i} \le 1
U = i = 1 ∑ n P i C i ≤ 1
当 U ≤ 1 U \le 1 U ≤ 1
注意
【情况 1】:D i ≤ P i D_i \le P_i D i ≤ P i
我们使用以下公式寻找任务 T i T_i T i 响应时间 R i ( n + 1 ) R^{(n+1)}_i R i ( n + 1 ) 最小不动点 R i ( ∗ ) R^{(*)}_i R i ( ∗ )
R i ( 0 ) = C i R i ( n + 1 ) = C i + ∑ j ∈ h p ( i ) ⌈ R i ( n ) P j ⌉ × C j \begin{aligned}
& R^{(0)}_i \quad = C_i \\
& R^{(n+1)}_i = C_i + \sum _{j\in hp(i)} \left \lceil \frac{R^{(n)}_i}{P_j} \right \rceil \times C_j
\end{aligned}
R i ( 0 ) = C i R i ( n + 1 ) = C i + j ∈ h p ( i ) ∑ ⌈ P j R i ( n ) ⌉ × C j
提示
使用之前研究过的任务 T 1 T_1 T 1 T 2 T_2 T 2
T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 2 ) T_1 (r_1:0, \; C_1:1, \; D_1:2, \; P_1:2) T 1 ( r 1 : 0 , C 1 : 1 , D 1 : 2 , P 1 : 2 ) T 2 ( r 2 : 0 , C 2 : 2 , D 2 : 5 , P 2 : 5 ) T_2 (r_2:0, \; C_2:2, \; D_2:5, \; P_2:5) T 2 ( r 2 : 0 , C 2 : 2 , D 2 : 5 , P 2 : 5 )
R 2 ( 0 ) = C 2 = 2 R 2 ( 1 ) = C 2 + ⌈ R 2 ( 0 ) P 1 ⌉ × C 1 = 2 + ⌈ 2 2 ⌉ × 1 = 3 R 2 ( 2 ) = C 2 + ⌈ R 2 ( 1 ) P 1 ⌉ × C 1 = 2 + ⌈ 3 2 ⌉ × 1 = 4 R 2 ( 3 ) = C 2 + ⌈ R 2 ( 2 ) P 1 ⌉ × C 1 = 2 + ⌈ 4 2 ⌉ × 1 = 4 = R 2 ( 2 ) = R 2 ( ∗ ) \begin{aligned}
& R^{(0)}_2 \quad = C_2 = 2\\
& R^{(1)}_2 \quad = C_2 + \left \lceil \frac{R^{(0)}_2}{P_1} \right \rceil \times C_1 = 2 + \left \lceil \frac{2}{2} \right \rceil \times 1 = 3 \\
& R^{(2)}_2 \quad = C_2 + \left \lceil \frac{R^{(1)}_2}{P_1} \right \rceil \times C_1 = 2 + \left \lceil \frac{3}{2} \right \rceil \times 1 = 4 \\
& R^{(3)}_2 \quad = C_2 + \left \lceil \frac{R^{(2)}_2}{P_1} \right \rceil \times C_1 = 2 + \left \lceil \frac{4}{2} \right \rceil \times 1 = 4 = R^{(2)}_2 = R^{(*)}_2
\end{aligned}
R 2 ( 0 ) = C 2 = 2 R 2 ( 1 ) = C 2 + ⌈ P 1 R 2 ( 0 ) ⌉ × C 1 = 2 + ⌈ 2 2 ⌉ × 1 = 3 R 2 ( 2 ) = C 2 + ⌈ P 1 R 2 ( 1 ) ⌉ × C 1 = 2 + ⌈ 2 3 ⌉ × 1 = 4 R 2 ( 3 ) = C 2 + ⌈ P 1 R 2 ( 2 ) ⌉ × C 1 = 2 + ⌈ 2 4 ⌉ × 1 = 4 = R 2 ( 2 ) = R 2 ( ∗ )
【情况 2】:D i > P i D_i > P_i D i > P i T i T_i T i
在这种情况下,必须计算这个工作 job k \text{job}_k job k 响应时间 R i ( n + 1 ) ( k ) R^{(n+1)}_i(k) R i ( n + 1 ) ( k ) t k t_k t k
因为我们需要:测试 k k k
R i ( ∗ ) ( k ) ≤ k × P i R^{(*)}_i(k) \le k \times P_i
R i ( ∗ ) ( k ) ≤ k × P i
"k k k
计算公式类比于【情况 1】,如下所示:
R i ( 0 ) ( k ) = k × C i R i ( n + 1 ) ( k ) = k × C i + ∑ j ∈ h p ( i ) ⌈ R i ( n ) ( k ) P j ⌉ × C j \begin{aligned}
& R^{(0)}_i(k) \quad = k \times C_i \\
& R^{(n+1)}_i(k) = k \times C_i + \sum _{j\in hp(i)} \left \lceil \frac{R^{(n)}_i(k)}{P_j} \right \rceil \times C_j
\end{aligned}
R i ( 0 ) ( k ) = k × C i R i ( n + 1 ) ( k ) = k × C i + j ∈ h p ( i ) ∑ ⌈ P j R i ( n ) ( k ) ⌉ × C j
下面,我们将给出另一个关于任务 T 1 T_1 T 1 T 2 T_2 T 2
T 1 ( r 1 : 0 , C 1 : 26 , D 1 : 70 , P 1 : 70 ) T_1 (r_1:0, \; C_1:26, \; D_1:70, \; P_1:70) T 1 ( r 1 : 0 , C 1 : 2 6 , D 1 : 7 0 , P 1 : 7 0 )
T 2 ( r 2 : 0 , C 2 : 62 , D 2 : 118 , P 2 : 100 ) T_2 (r_2:0, \; C_2:62, \; D_2:118, \; P_2:100) T 2 ( r 2 : 0 , C 2 : 6 2 , D 2 : 1 1 8 , P 2 : 1 0 0 )
计算过程:
对于任务 T 1 T_1 T 1
R 1 ( 0 ) = C 1 = 26 R 1 ( 1 ) = C 1 = 26 = R 1 ( 0 ) = R 1 ( ∗ ) \begin{aligned}
& R^{(0)}_1 \quad = C_1 = 26\\
& R^{(1)}_1 \quad = C_1 = 26 = R^{(0)}_1 = R^{(*)}_1
\end{aligned}
R 1 ( 0 ) = C 1 = 2 6 R 1 ( 1 ) = C 1 = 2 6 = R 1 ( 0 ) = R 1 ( ∗ )
对于任务 T 2 T_2 T 2 T 1 T_1 T 1
R 2 ( 0 ) ( 1 ) = C 2 = 62 R 2 ( 1 ) ( 1 ) = C 2 + ⌈ R 2 ( 0 ) ( 1 ) P 1 ⌉ × C 1 = 62 + ⌈ 62 70 ⌉ × 26 = 88 R 2 ( 2 ) ( 1 ) = C 2 + ⌈ R 2 ( 1 ) ( 1 ) P 1 ⌉ × C 1 = 62 + ⌈ 88 70 ⌉ × 26 = 114 R 2 ( 3 ) ( 1 ) = C 2 + ⌈ R 2 ( 2 ) ( 1 ) P 1 ⌉ × C 1 = 62 + ⌈ 114 70 ⌉ × 26 = 114 = R 2 ( 2 ) ( 1 ) = R 2 ( ∗ ) ( 1 ) ∵ R 2 ( ∗ ) ( 1 ) > k × P 2 ,不满足要求 ∴ 令 k=2,继续计算 R 2 ( ∗ ) ( 2 ) = 202 > 2 × P 2 ( = 200 ) R 2 ( ∗ ) ( 3 ) = 316 > 3 × P 2 ( = 300 ) R 2 ( ∗ ) ( 4 ) = 404 > 4 × P 2 ( = 400 ) R 2 ( ∗ ) ( 5 ) = 518 > 5 × P 2 ( = 500 ) R 2 ( ∗ ) ( 6 ) = 606 > 6 × P 2 ( = 600 ) R 2 ( ∗ ) ( 7 ) = 694 < 7 × P 2 ( = 700 ) 满足条件,且最后一个工作的响应时间为 94 \begin{aligned}
& R^{(0)}_2(1) \quad = C_2 = 62\\
& R^{(1)}_2(1) \quad = C_2 + \left \lceil \frac{R^{(0)}_2(1)}{P_1} \right \rceil \times C_1 = 62 + \left \lceil \frac{62}{70} \right \rceil \times 26 = 88 \\
& R^{(2)}_2(1) \quad = C_2 + \left \lceil \frac{R^{(1)}_2(1)}{P_1} \right \rceil \times C_1 = 62 + \left \lceil \frac{88}{70} \right \rceil \times 26 = 114 \\
& R^{(3)}_2(1) \quad = C_2 + \left \lceil \frac{R^{(2)}_2(1)}{P_1} \right \rceil \times C_1 = 62 + \left \lceil \frac{114}{70} \right \rceil \times 26 = 114 = R^{(2)}_2(1) = R^{(*)}_2(1)\\
& \because R^{(*)}_2(1) > k \times P_2 \text{,不满足要求}\quad \therefore\text{令 k=2,继续计算}\\
\\
& R^{(*)}_2(2) = 202 > 2 \times P_2(=200) \\
& R^{(*)}_2(3) = 316 > 3 \times P_2(=300) \\
& R^{(*)}_2(4) = 404 > 4 \times P_2(=400) \\
& R^{(*)}_2(5) = 518 > 5 \times P_2(=500) \\
& R^{(*)}_2(6) = 606 > 6 \times P_2(=600) \\
& R^{(*)}_2(7) = 694 < 7 \times P_2(=700) \quad \text{满足条件,且最后一个工作的响应时间为 94}
\end{aligned}
R 2 ( 0 ) ( 1 ) = C 2 = 6 2 R 2 ( 1 ) ( 1 ) = C 2 + ⌈ P 1 R 2 ( 0 ) ( 1 ) ⌉ × C 1 = 6 2 + ⌈ 7 0 6 2 ⌉ × 2 6 = 8 8 R 2 ( 2 ) ( 1 ) = C 2 + ⌈ P 1 R 2 ( 1 ) ( 1 ) ⌉ × C 1 = 6 2 + ⌈ 7 0 8 8 ⌉ × 2 6 = 1 1 4 R 2 ( 3 ) ( 1 ) = C 2 + ⌈ P 1 R 2 ( 2 ) ( 1 ) ⌉ × C 1 = 6 2 + ⌈ 7 0 1 1 4 ⌉ × 2 6 = 1 1 4 = R 2 ( 2 ) ( 1 ) = R 2 ( ∗ ) ( 1 ) ∵ R 2 ( ∗ ) ( 1 ) > k × P 2 ,不满足要求 ∴ 令 k=2 ,继续计算 R 2 ( ∗ ) ( 2 ) = 2 0 2 > 2 × P 2 ( = 2 0 0 ) R 2 ( ∗ ) ( 3 ) = 3 1 6 > 3 × P 2 ( = 3 0 0 ) R 2 ( ∗ ) ( 4 ) = 4 0 4 > 4 × P 2 ( = 4 0 0 ) R 2 ( ∗ ) ( 5 ) = 5 1 8 > 5 × P 2 ( = 5 0 0 ) R 2 ( ∗ ) ( 6 ) = 6 0 6 > 6 × P 2 ( = 6 0 0 ) R 2 ( ∗ ) ( 7 ) = 6 9 4 < 7 × P 2 ( = 7 0 0 ) 满足条件,且最后一个工作的响应时间为 94
速率单调 周期任务 P P P 1 P \frac{1}{P} P 1
该策略需要知道欲执行任务的周期 P P P
而且要为每个任务 T i T_i T i P i P_i P i 任务的周期越小,优先级就越高
前面我们已经介绍过有关处理器利用率 U U U 速率单调算法下是可调度的【必要】条件
U ≤ 1 U \le 1
U ≤ 1
我们通过对周期任务的分析,我们得出周期任务在速率单调算法下是可调度的【充分】条件
U = ∑ i = 1 n C i P i ≤ n × ( 2 1 n − 1 ) U = \sum _{i=1} ^n \frac{C_i}{P_i} \le n \times (2^{\frac{1}{n}} -1)
U = i = 1 ∑ n P i C i ≤ n × ( 2 n 1 − 1 )
下面,我们给出几个常见的周期任务 T i , i ∈ [ 0... n ] T_i,i\in[0...n] T i , i ∈ [ 0 . . . n ] 单调速率 可调度 处理器使用率 b o u n d bound b o u n d
n n n 1
2
3
4
5
6
10
∞ \infin ∞
b o u n d bound b o u n d 1 1 1 0.828 0.828 0 . 8 2 8 0.779 0.779 0 . 7 7 9 0.756 0.756 0 . 7 5 6 0.743 0.743 0 . 7 4 3 0.734 0.734 0 . 7 3 4 0.717 0.717 0 . 7 1 7 0.693 0.693 0 . 6 9 3
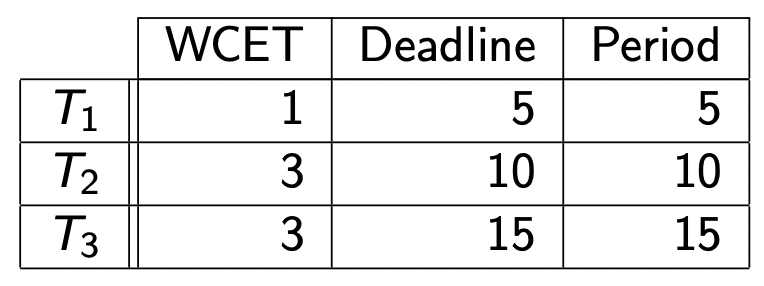
我们给出一个使用速率单调法来确定静态优先级的可调度的例子:
(1)首先,我们可以先计算一下任务 T 1 T_1 T 1 T 2 T_2 T 2 T 3 T_3 T 3 U U U
U = ∑ i = 1 n C i P i = 1 5 + 3 10 + 3 15 = 7 10 < 0.779 U = \sum _{i=1} ^n \frac{C_i}{P_i} = \frac{1}{5} + \frac{3}{10} + \frac{3}{15} = \frac{7}{10} < 0.779
U = i = 1 ∑ n P i C i = 5 1 + 1 0 3 + 1 5 3 = 1 0 7 < 0 . 7 7 9
所以,该任务可以被成功调度。
(2)其次,通过速率单调法 T 1 T_1 T 1 T 2 T_2 T 2 T 3 T_3 T 3 静态优先级
Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 ) \text{Priority}(T_1) > \text{Priority}(T_2) > \text{Priority}(T_3)
Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 )
我们可以画出调度时序图(Scheduling sequence):
(3)最后,我们可以计算出各个任务的响应时间分析
t 0 = ∑ i = 1.. j , j ∈ h p ( i ) C i t n + 1 = ∑ i = 1.. j , j ∈ h p ( i ) ⌈ t n P i ⌉ × C i iff R i ( ∗ ) ≤ D i , then OK , else KO \begin{aligned}
& t_0 = \sum _{i=1..j,j\in hp(i)} C_i\\
& t_{n+1} = \sum _{i=1..j,j\in hp(i)} \left \lceil \frac{t_{n}}{P_i} \right \rceil \times C_i\\
& \text{iff } R^{(*)}_i \le D_i, \quad \text{then OK}, \quad \text{else KO}
\end{aligned}
t 0 = i = 1 . . j , j ∈ h p ( i ) ∑ C i t n + 1 = i = 1 . . j , j ∈ h p ( i ) ∑ ⌈ P i t n ⌉ × C i iff R i ( ∗ ) ≤ D i , then OK , else KO
注意
t n t_n t n T 1 T_1 T 1 T 2 T_2 T 2 T 3 T_3 T 3
t 0 t_0 t 0 C 1 = 1 C_1 = 1 C 1 = 1 C 1 + C 2 = 4 C_1 + C_2 = 4 C 1 + C 2 = 4 C 1 + C 2 + C 3 = 7 C_1 + C_2 + C_3 = 7 C 1 + C 2 + C 3 = 7
t 1 t_1 t 1 ⌈ t 0 P 1 ⌉ C 1 = 1 \left \lceil \frac{t_{0}}{P_1} \right \rceil C_1 = 1 ⌈ P 1 t 0 ⌉ C 1 = 1 ⌈ t 0 P 1 ⌉ C 1 + ⌈ t 0 P 2 ⌉ C 2 = 4 \left \lceil \frac{t_{0}}{P_1} \right \rceil C_1 + \left \lceil \frac{t_{0}}{P_2} \right \rceil C_2 = 4 ⌈ P 1 t 0 ⌉ C 1 + ⌈ P 2 t 0 ⌉ C 2 = 4 ⌈ t 0 P 1 ⌉ C 1 + ⌈ t 0 P 2 ⌉ C 2 + ⌈ t 0 P 3 ⌉ C 3 = 8 \left \lceil \frac{t_{0}}{P_1} \right \rceil C_1 + \left \lceil \frac{t_{0}}{P_2} \right \rceil C_2 + \left \lceil \frac{t_{0}}{P_3} \right \rceil C_3 = 8 ⌈ P 1 t 0 ⌉ C 1 + ⌈ P 2 t 0 ⌉ C 2 + ⌈ P 3 t 0 ⌉ C 3 = 8
t 2 t_2 t 2 -
-
⌈ t 1 P 1 ⌉ C 1 + ⌈ t 1 P 2 ⌉ C 2 + ⌈ t 1 P 3 ⌉ C 3 = 8 \left \lceil \frac{t_{1}}{P_1} \right \rceil C_1 + \left \lceil \frac{t_{1}}{P_2} \right \rceil C_2 + \left \lceil \frac{t_{1}}{P_3} \right \rceil C_3 = 8 ⌈ P 1 t 1 ⌉ C 1 + ⌈ P 2 t 1 ⌉ C 2 + ⌈ P 3 t 1 ⌉ C 3 = 8
t 3 t_3 t 3 -
-
-
OK
OK
OK
在静态优先级算法中,尤其是速率单调法中,我们得出了一个可调度的充分条件:
当处理器使用率 U ≤ n × ( 2 1 n − 1 ) U \le n \times (2^ {\frac{1}{n}} -1) U ≤ n × ( 2 n 1 − 1 )
显然,这个上界值并不是很好。我们为了使这个上界值接近 ≤ 1 \le 1 ≤ 1 单调截止时间法 截止时间 D D D
但是,这种单调截止时间法并不是最佳的静态优先级分配。所以我们提出了动态的优先级分配策略,最早截止时间优先
提示:课件 P 38 P_{38} P 3 8
一个固定优先级(静态优先级 动态优先级 容易实现
但是,动态优先级 EDF U U U 100 % 100% 1 0 0 % 静态优先级 单调速率 RM U U U 69 % 69% 6 9 %
最早截止时间优先 EDF 周期性和非周期性任务
在每一个新的就绪状态,调度器都是从那些已就绪但还没有完全处理完毕的任务中选择最早截止时间的任务
EDF 抢占式 单处理器 最优的调度算法
【对于周期任务 T T T D ≤ P D \le P D ≤ P
可调度的充分必要
U = ∑ i = 1 n C i P i ≤ 1 U = \sum _{i=1}^n \frac{C_i}{P_i} \le 1
U = i = 1 ∑ n P i C i ≤ 1
【对于周期任务 T T T D > P D > P D > P
可调度性分析会更加复杂:我们需要引入需求函数 d f ( ) df() d f ( )
关于需求函数 d f ( ) df() d f ( )
“Definition:
The demand function for a task T i T_i T i [ t 1 , t 2 ] [t_1, t_2] [ t 1 , t 2 ] [ t 1 , t 2 ] [t_1, t_2] [ t 1 , t 2 ] T i T_i T i
d f i ( t 1 , t 2 ) = ∑ a i j ≥ t 1 , d i j ≤ t 2 C i j df_i(t_1, t_2) = \sum _{a_{ij} \ge t_1 , d_{ij} \le t_2} C_{ij}
d f i ( t 1 , t 2 ) = a i j ≥ t 1 , d i j ≤ t 2 ∑ C i j
For the entire task set:
d f ( t 1 , t 2 ) = ∑ i = 1 n d f i ( t 1 , t 2 ) df(t_1, t_2) = \sum _{i=1} ^n df_i(t_1, t_2)
d f ( t 1 , t 2 ) = i = 1 ∑ n d f i ( t 1 , t 2 )
此时我们先给出,在一般情况下,对于该问题,任务可以被 EDF 成功调度的充分必要条件是:
∀ t 1 , t 2 d f ( t 1 , t 2 ) ≤ t 2 − t 1 \forall t_1, t_2 \qquad df(t_1, t_2) \le t_2 − t_1
∀ t 1 , t 2 d f ( t 1 , t 2 ) ≤ t 2 − t 1
但是我们无法计算所有的 [ t 1 , t 2 ] [t_1,t_2] [ t 1 , t 2 ]
个人理解
对于任务 T i T_i T i d f i ( ) df_i() d f i ( ) 同一个周期内 就绪时刻 向上的箭头 ↑ \uparrow ↑ 截止时刻 向下的箭头 ↓ \downarrow ↓ [ t 1 , t 2 ] [t_1,t_2] [ t 1 , t 2 ] C i C_i C i 和
对于所有任务 d f ( ) df() d f ( ) C C C
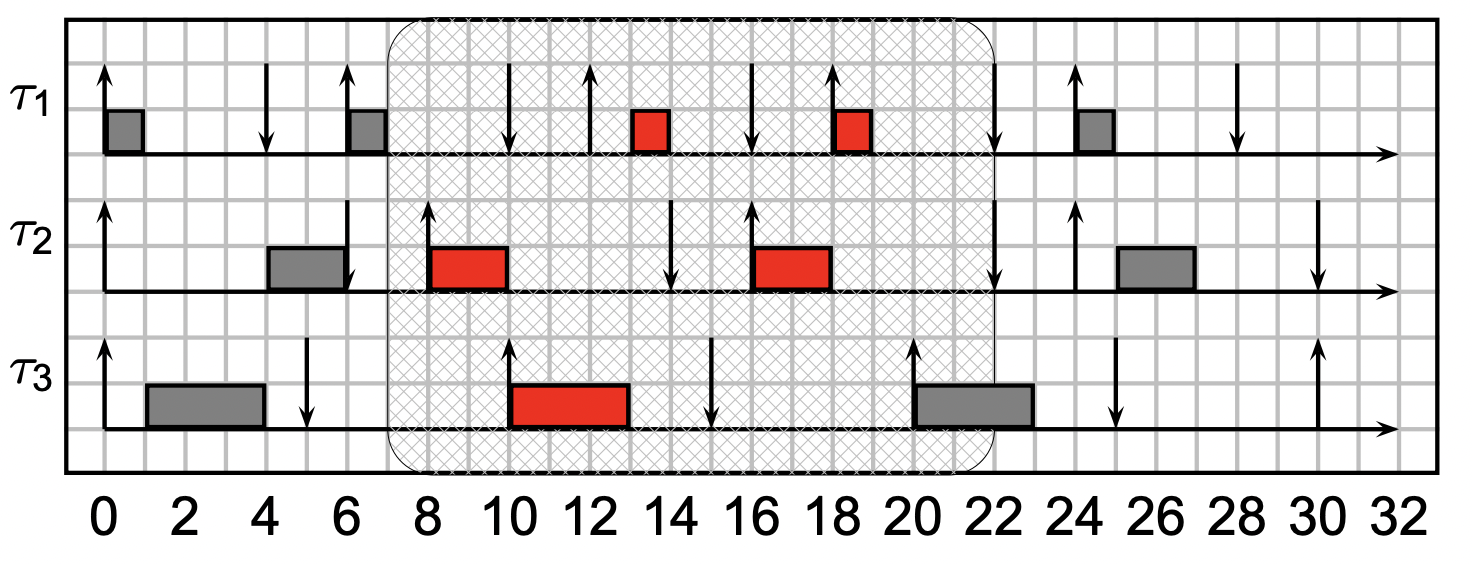
示例:给出如下任务
T 1 = ( 1 , 4 , 6 ) , T 2 = ( 2 , 6 , 8 ) , T 3 = ( 3 , 5 , 10 ) T_1 = (1, 4, 6),\quad T_2 = (2, 6, 8), \quad T_3 = (3, 5, 10) T 1 = ( 1 , 4 , 6 ) , T 2 = ( 2 , 6 , 8 ) , T 3 = ( 3 , 5 , 1 0 )
我们即可画出调度时序图:
当计算 d f ( 7 , 22 ) df(7,22) d f ( 7 , 2 2 )
d f ( 7 , 22 ) = 2 × C 1 + 2 × C 2 + 1 × C 3 = 9 ; df(7,22) = 2 \times C_1 + 2 \times C_2 + 1 \times C_3 = 9;
d f ( 7 , 2 2 ) = 2 × C 1 + 2 × C 2 + 1 × C 3 = 9 ;
计算 d f ( 3 , 13 ) df(3,13) d f ( 3 , 1 3 )
d f ( 3 , 13 ) = 1 × C 1 + 0 × C 2 + 0 × C 3 = 1 ; df(3,13) = 1 \times C_1 + 0 \times C_2 + 0 \times C_3 = 1;
d f ( 3 , 1 3 ) = 1 × C 1 + 0 × C 2 + 0 × C 3 = 1 ;
计算 d f ( 10 , 25 ) df(10,25) d f ( 1 0 , 2 5 )
d f ( 10 , 25 ) = 2 × C 1 + 1 × C 2 + 2 × C 3 = 10 ; df(10,25) = 2 \times C_1 + 1 \times C_2 + 2 \times C_3 = 10;
d f ( 1 0 , 2 5 ) = 2 × C 1 + 1 × C 2 + 2 × C 3 = 1 0 ;
对于一系列同步的周期任务 T T T 截止时刻 L L L d f ( 0 , L ) df(0,L) d f ( 0 , L ) 临界需求函数 dbf
d b f ( L ) = max t ( d f ( t , t + L ) ) = d f ( 0 , L ) dbf(L) = \max _t(df(t,t+L)) = df(0,L)
d b f ( L ) = t max ( d f ( t , t + L ) ) = d f ( 0 , L )
之前我们说过,对于一系列周期性任务,我们可以找到他们周期的最小公倍数 L C M 1 ≤ i ≤ n ( P i ) LCM_{1\le i \le n}(P_i) L C M 1 ≤ i ≤ n ( P i )
H = L C M 1 ≤ i ≤ n ( P i ) H = LCM_{1\le i \le n}(P_i)
H = L C M 1 ≤ i ≤ n ( P i )
然后在这个最小公倍周期 H H H 所有截止时间构成的集合 D e a d l i n e S e t DeadlineSet D e a d l i n e S e t
∀ L ∈ D e a d l i n e T e s t , D e a d l i n e S e t ⊂ 集 合 [ 0 , H ] \forall L \in DeadlineTest, \quad DeadlineSet \subset 集合[0,H]
∀ L ∈ D e a d l i n e T e s t , D e a d l i n e S e t ⊂ 集 合 [ 0 , H ]
在此情况下,任务可以被 EDF 成功调度的充分必要
∀ L ∈ D e a d l i n e S e t , d b f ( L ) ≤ L \forall L \in DeadlineSet, \quad dbf(L) \le L
∀ L ∈ D e a d l i n e S e t , d b f ( L ) ≤ L
而对于异步情况来讲,同步是其中最特殊的情况,也是最坏的情况。所以异步的周期任务也满足该条件。
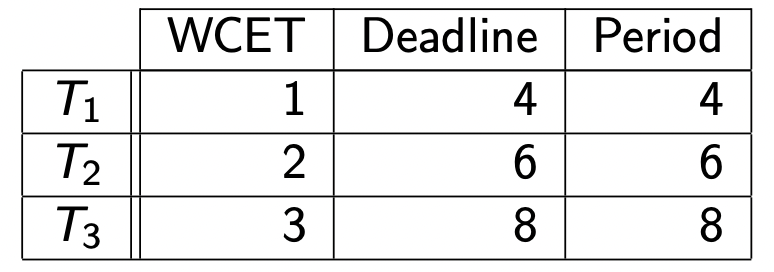
给出如下任务:
计算处理器使用率 U U U
U = ∑ i = 1 n C i P i = 1 4 + 2 6 + 3 8 = 23 24 U = \sum _{i=1}^n \frac{C_i}{P_i} = \frac{1}{4} + \frac{2}{6} + \frac{3}{8} = \frac{23}{24}
U = i = 1 ∑ n P i C i = 4 1 + 6 2 + 8 3 = 2 4 2 3
计算最小公倍周期 H H H
H = L C M 1 ≤ i ≤ n ( P i ) = 24 H = LCM_{1\le i \le n}(P_i)=24
H = L C M 1 ≤ i ≤ n ( P i ) = 2 4
列出 D e a d l i n e S e t DeadlineSet D e a d l i n e S e t
D e a d l i n e S e t = { 4 , 6 , 8 , 12 , 16 , 18 , 20 , 24 } DeadlineSet= \{4,6,8,12,16,18,20,24\}
D e a d l i n e S e t = { 4 , 6 , 8 , 1 2 , 1 6 , 1 8 , 2 0 , 2 4 }
计算所有的临界需求函数 d b f ( L ) dbf(L) d b f ( L )
d b f ( 4 ) = d f ( 0 , 4 ) = 1 × C 1 = 1 dbf(4) = df(0,4) = 1 \times C_1 = 1 d b f ( 4 ) = d f ( 0 , 4 ) = 1 × C 1 = 1 d b f ( 6 ) = d f ( 0 , 6 ) = 1 × C 1 + 1 × C 2 = 3 dbf(6) = df(0,6) = 1 \times C_1 + 1 \times C_2 = 3 d b f ( 6 ) = d f ( 0 , 6 ) = 1 × C 1 + 1 × C 2 = 3 d b f ( 8 ) = d f ( 0 , 8 ) = 2 × C 1 + 1 × C 2 + 1 × C 3 = 7 dbf(8) = df(0,8) = 2 \times C_1 + 1 \times C_2 + 1 \times C_3= 7 d b f ( 8 ) = d f ( 0 , 8 ) = 2 × C 1 + 1 × C 2 + 1 × C 3 = 7 d b f ( 12 ) = d f ( 0 , 12 ) = 3 × C 1 + 2 × C 2 + 1 × C 3 = 10 dbf(12) = df(0,12) = 3 \times C_1 + 2 \times C_2 + 1 \times C_3= 10 d b f ( 1 2 ) = d f ( 0 , 1 2 ) = 3 × C 1 + 2 × C 2 + 1 × C 3 = 1 0 d b f ( 16 ) = d f ( 0 , 16 ) = 4 × C 1 + 2 × C 2 + 2 × C 3 = 14 dbf(16) = df(0,16) = 4 \times C_1 + 2 \times C_2 + 2 \times C_3= 14 d b f ( 1 6 ) = d f ( 0 , 1 6 ) = 4 × C 1 + 2 × C 2 + 2 × C 3 = 1 4 d b f ( 18 ) = d f ( 0 , 18 ) = 4 × C 1 + 3 × C 2 + 2 × C 3 = 16 dbf(18) = df(0,18) = 4 \times C_1 + 3 \times C_2 + 2 \times C_3= 16 d b f ( 1 8 ) = d f ( 0 , 1 8 ) = 4 × C 1 + 3 × C 2 + 2 × C 3 = 1 6 d b f ( 20 ) = d f ( 0 , 20 ) = 5 × C 1 + 3 × C 2 + 2 × C 3 = 17 dbf(20) = df(0,20) = 5 \times C_1 + 3 \times C_2 + 2 \times C_3= 17 d b f ( 2 0 ) = d f ( 0 , 2 0 ) = 5 × C 1 + 3 × C 2 + 2 × C 3 = 1 7 d b f ( 24 ) = d f ( 0 , 24 ) = 6 × C 1 + 4 × C 2 + 3 × C 3 = 23 dbf(24) = df(0,24) = 6 \times C_1 + 4 \times C_2 + 3 \times C_3= 23 d b f ( 2 4 ) = d f ( 0 , 2 4 ) = 6 × C 1 + 4 × C 2 + 3 × C 3 = 2 3
满足被 EDF 成功调度的充分必要
∀ L ∈ D e a d l i n e S e t , d b f ( L ) ≤ L \forall L \in DeadlineSet, \quad dbf(L) \le L
∀ L ∈ D e a d l i n e S e t , d b f ( L ) ≤ L
对于非周期性(Aperiodic)任务来说,我们应该从两个方面来分析它们:
无截止时间 确保周期任务可调度 尽量缩短非周期任务的响应时间 有截止时间 验收测试
若不行,可以直接拒绝该任务或者停止一个最不“重要”的任务
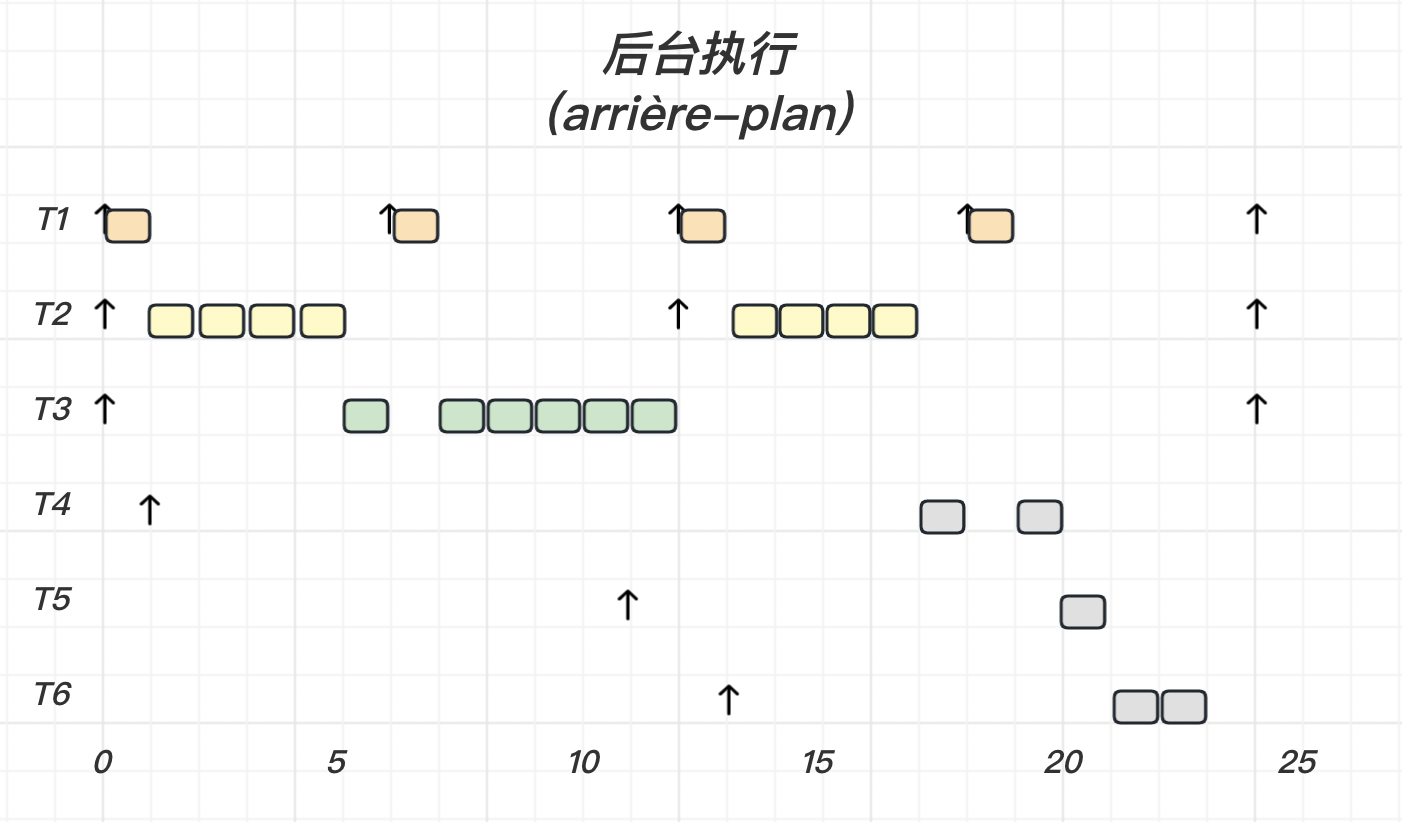
后台执行
使用先前提出的算法之一,为周期性任务 调度周期性任务
在***没有周期性任务的间隙(idle)*** 安排就绪的非周期任务 非周期性 相同的最低优先级
非周期任务按照“先到先服务
注意
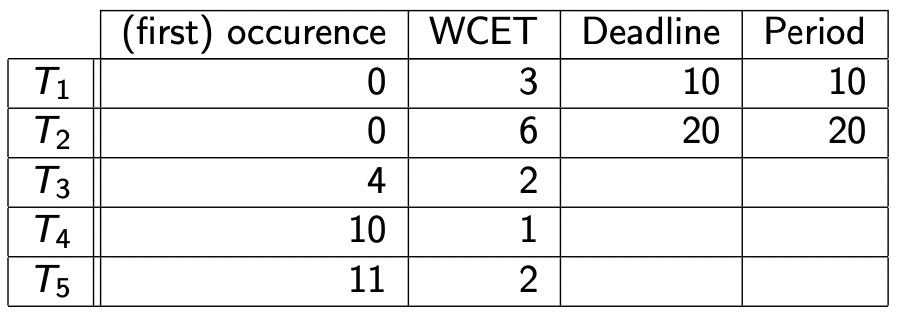
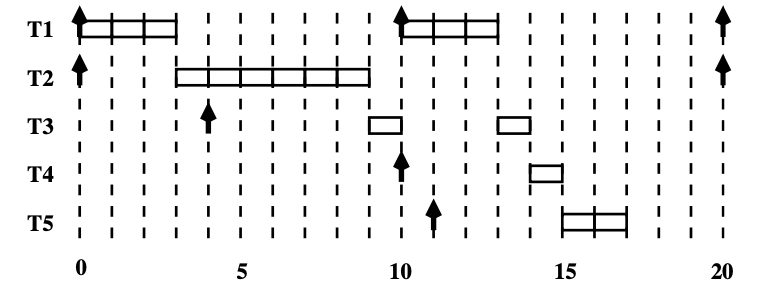
【示例】
我们使用后台执行
可以看到,任务 T 1 T_1 T 1 T 2 T_2 T 2 速率单调 T 3 T_3 T 3 T 4 T_4 T 4 T 5 T_5 T 5
画出调度时序图:
我们为了尽量缩短非周期性任务的响应时间,在此,我们引入服务器(Server)和预算(Budget)的概念:
服务器 服务器 周期任务 非周期任务的工作封装进服务器
服务器 较短的周期 P s P_s P s
预算 预算 服务器 C s C_{s} C s
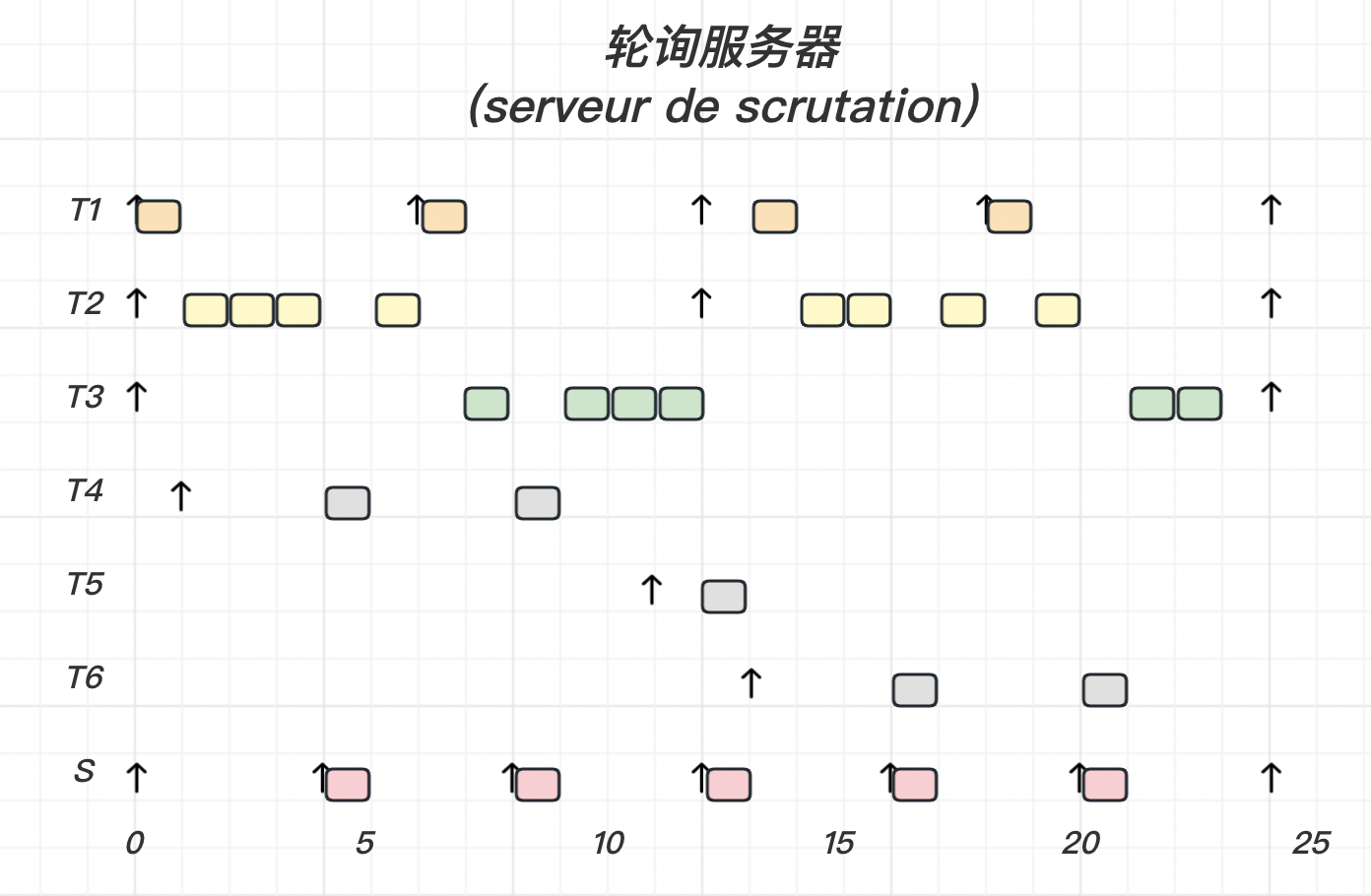
轮询服务器(serveur de scrutation)法的策略如下:
1 2 3 4 5 6 7 8 9 每次服务器获取处理器资源: Budget <- C_s; 下一次获取处理器资源的时间 <- 当前时间 + P_s; While( 有挂起或就绪的非周期任务 && Budget>0 ) : 执行一个单位时间的最早挂起或就绪的非周期任务; Budget <- Budget - 1; EndWhile Budget <- 0; // 若不满足while的执行条, 则直接置0, 从而结束本周期服务器的执行 释放处理器资源
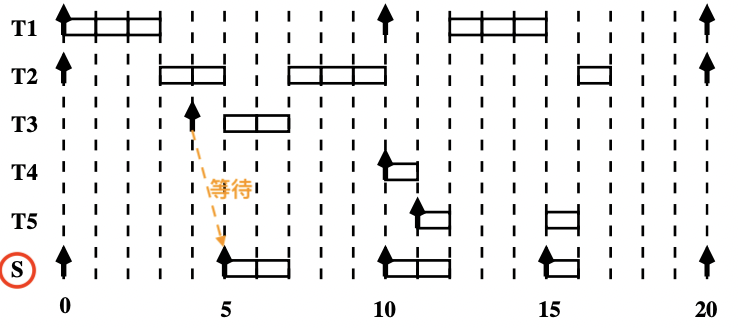
【示例】
我们使用轮询服务器 速率单调法
任务 T 1 T_1 T 1 T 2 T_2 T 2 S S S
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 ) \text{Priority}(S) > \text{Priority}(T_1) > \text{Priority}(T_2)
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 )
画出调度时序图:
关于结果的一点解释:
0 时刻时,S S S 没有挂起或就绪的非周期任务 立即将Budget 置 0 并释放处理器 等待下一个周期
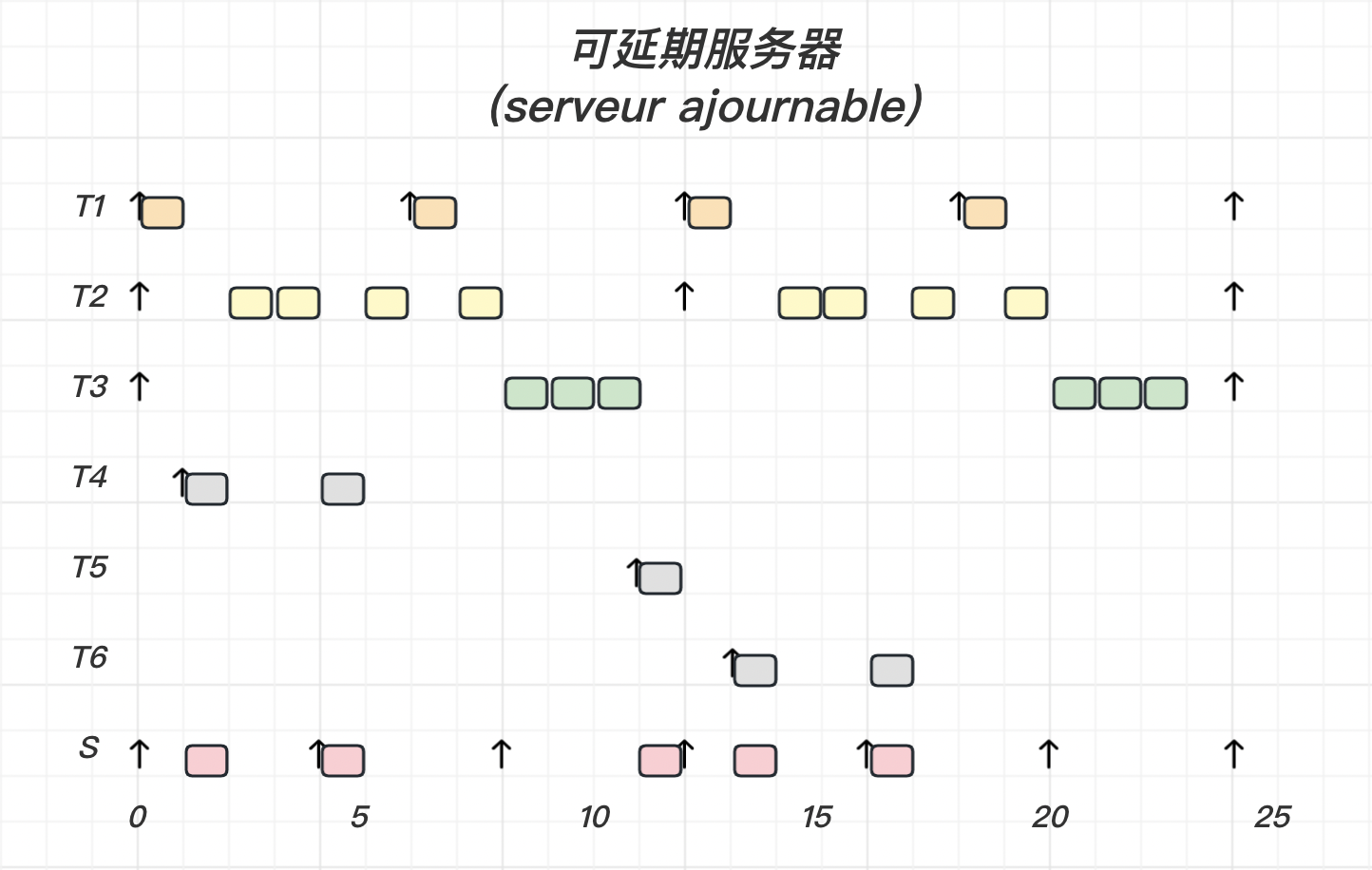
与轮询服务器不同,可延期服务器 保留其 Budget
可延期服务器(serveur ajournable)法的策略如下:
1 2 3 4 5 6 7 Budget <- C_s; 下一次获取处理器资源的时间 <- 当前时间 + P_s; While( 有挂起或就绪的非周期任务 && Budget>0 ) : 执行一个单位时间的最早挂起或就绪的非周期任务; Budget <- Budget - 1; EndWhile
当服务器没有获取处理器资源,但是有非周期任务就绪 有剩余的 Budget
1 2 3 4 While( 有挂起或就绪的非周期任务 && Budget>0 ) : 执行一个单位时间的最早挂起或就绪的非周期任务; Budget <- Budget - 1; EndWhile
注意 ⚠️:
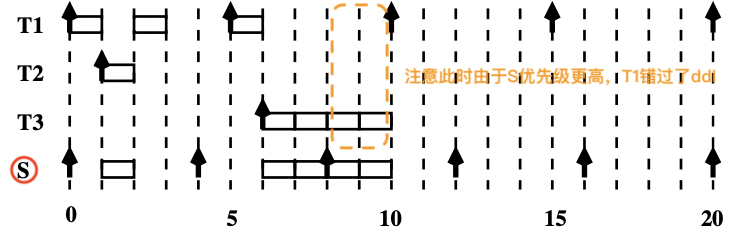
需要注意的是,这种策略可能导致周期任务错过 Deadline
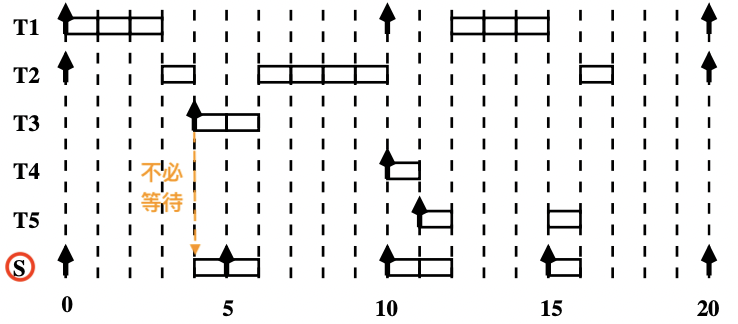
【示例】
我们使用可延期服务器
任务 T 1 T_1 T 1 T 2 T_2 T 2 S S S
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 ) \text{Priority}(S) > \text{Priority}(T_1) > \text{Priority}(T_2)
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 )
画出调度时序图:
关于结果的一点解释:
0 时刻时,S S S 立即释放处理器 本周期内 监听 之后是否有就绪的非周期任务
4 时刻时,非周期任务 T 3 T_3 T 3 T 3 T_3 T 3
【示例:导致周期任务错过 ddl
画出调度时序图:
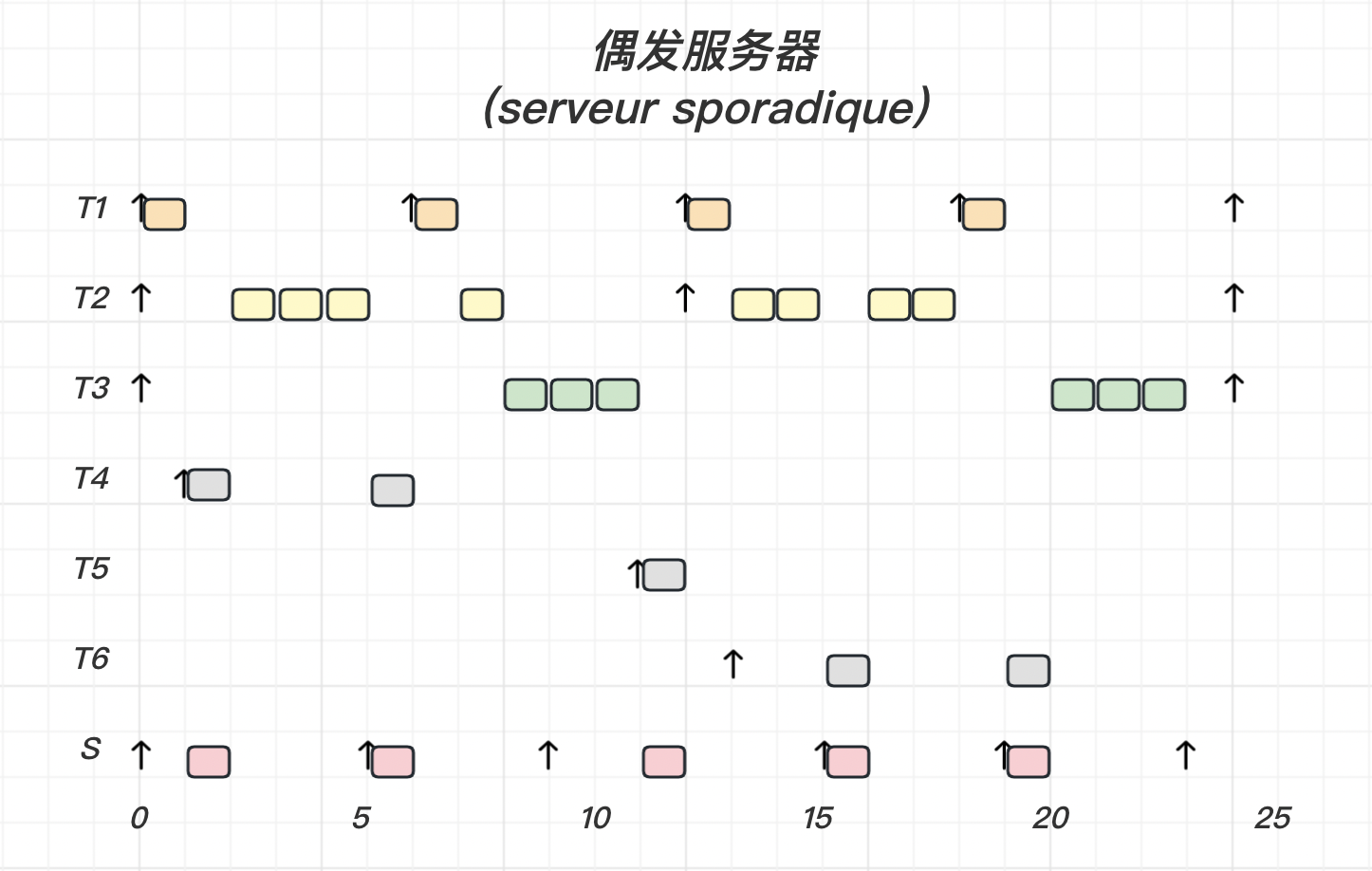
这种调度方式与前两种最显著的区别,在于周期的更新
在之前的版本中,周期的更新是固定
调度策略如下:
1 2 3 4 5 6 7 8 9 10 11 Budget <- C_s; If (有挂起或就绪的非周期任务) then 下一次获取处理器资源的时间 <- 当前时间 + P_s; While( 有挂起或就绪的非周期任务 && Budget>0 ) : 执行一个单位时间的最早挂起或就绪的非周期任务; Budget <- Budget - 1; EndWhile EndIf
当服务器没有获取处理器资源,但是有非周期任务就绪 有剩余的 Budget
1 2 3 4 5 6 7 8 If ( Budget == C_s ) then 下一次获取处理器资源的时间 <- 当前时间 + P_s; EndIf While( 有挂起或就绪的非周期任务 && Budget>0 ) : 执行一个单位时间的最早挂起或就绪的非周期任务; Budget <- Budget - 1; EndWhile
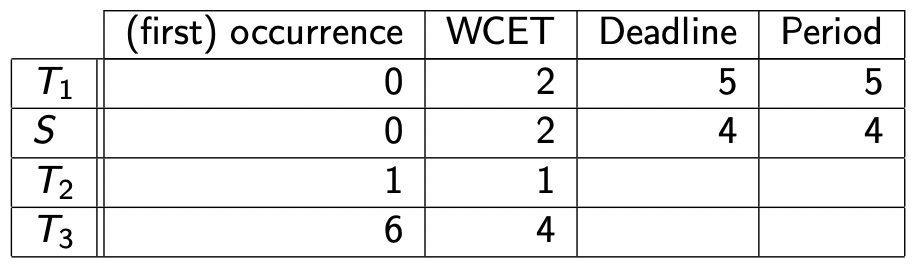
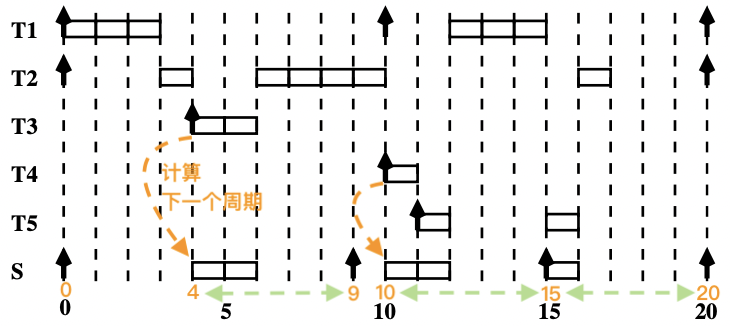
【示例】
我们使用可延期服务器
任务 T 1 T_1 T 1 T 2 T_2 T 2 S S S
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 ) \text{Priority}(S) > \text{Priority}(T_1) > \text{Priority}(T_2)
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 )
画出调度时序图:
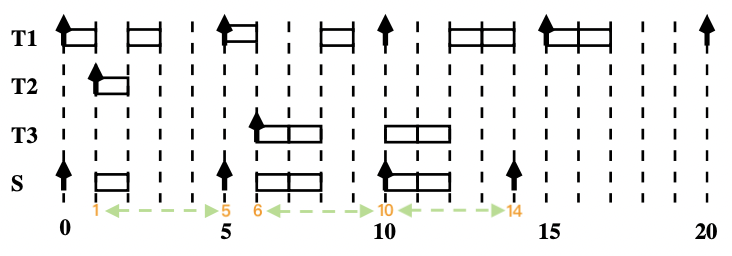
【示例 2】
我们继续研究上一节中导致周期任务错过 ddl 的例子:
画出调度时序图:
周期任务错过 ddl 的问题解决。
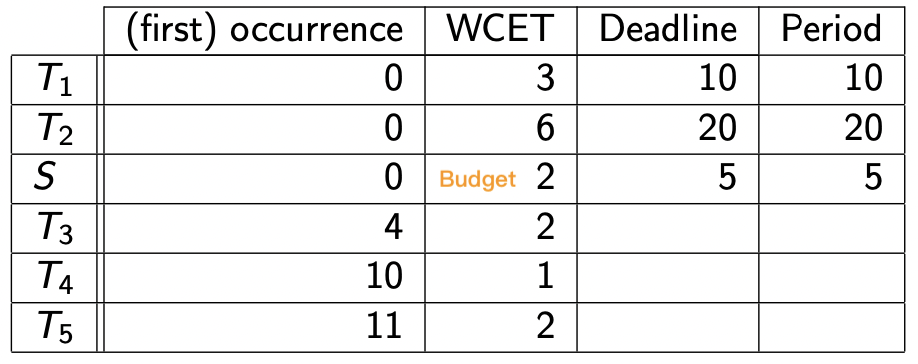
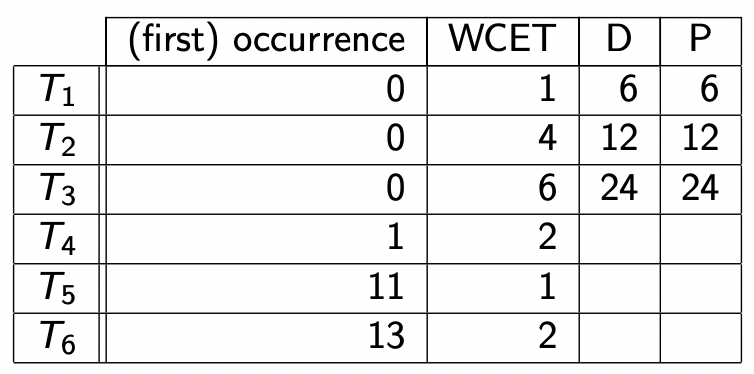
下面我们用一道例题将这四种不同的无截止时间的非周期任务调度放在一起比较:
下面的所有周期任务均使用速率单调法
关于服务器的信息 P s = 4 P_s = 4 P s = 4 Budget = 1 \text{Budget} = 1 Budget = 1
任务 T 1 T_1 T 1 T 2 T_2 T 2 T 3 T_3 T 3
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 ) \text{Priority}(S) > \text{Priority}(T_1) > \text{Priority}(T_2) > \text{Priority}(T_3)
Priority ( S ) > Priority ( T 1 ) > Priority ( T 2 ) > Priority ( T 3 )
画出调度时序图:
后台执行(arrière-plan)
轮询服务器(serveur de scrutation)
可延期服务器(serveur ajournable)
偶发服务器(serveur sporadique)
除了处理器资源外,任务在执行的过程中还需要访问共享的临界区资源 互斥方式 完成所有临界区资源访问后,后才会释放这些资源
在这种约定下,任务调度会出现两种问题:
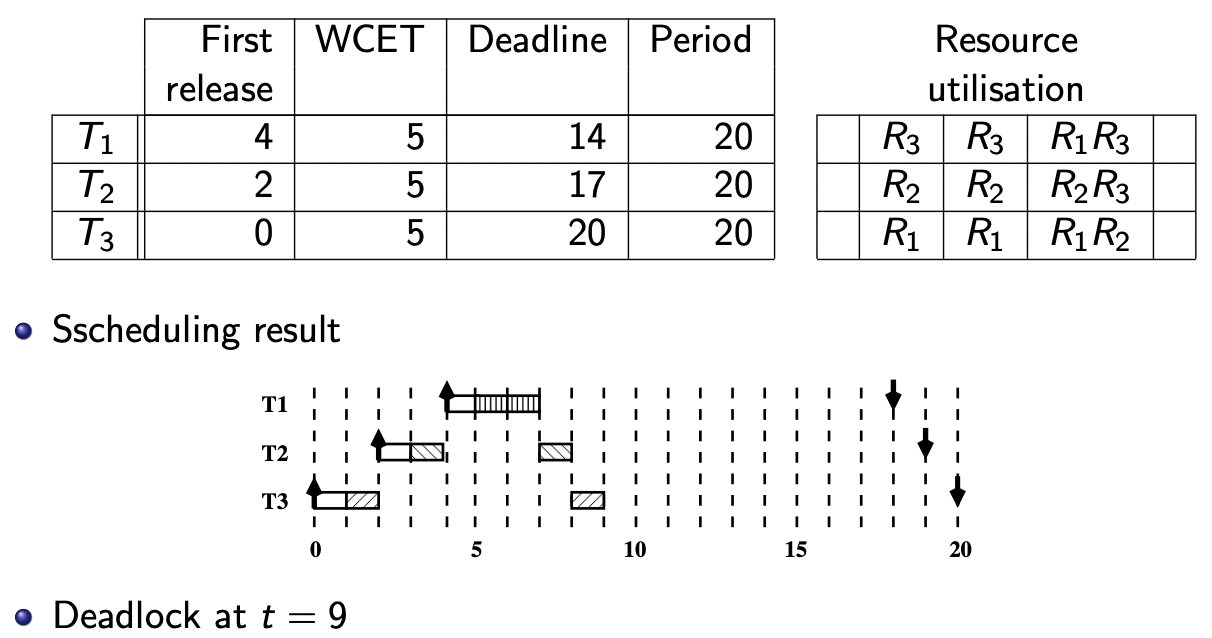
死锁
可以通过一种资源分配机制(resource allocation mechanism)防止死锁的产生
【死锁例子】
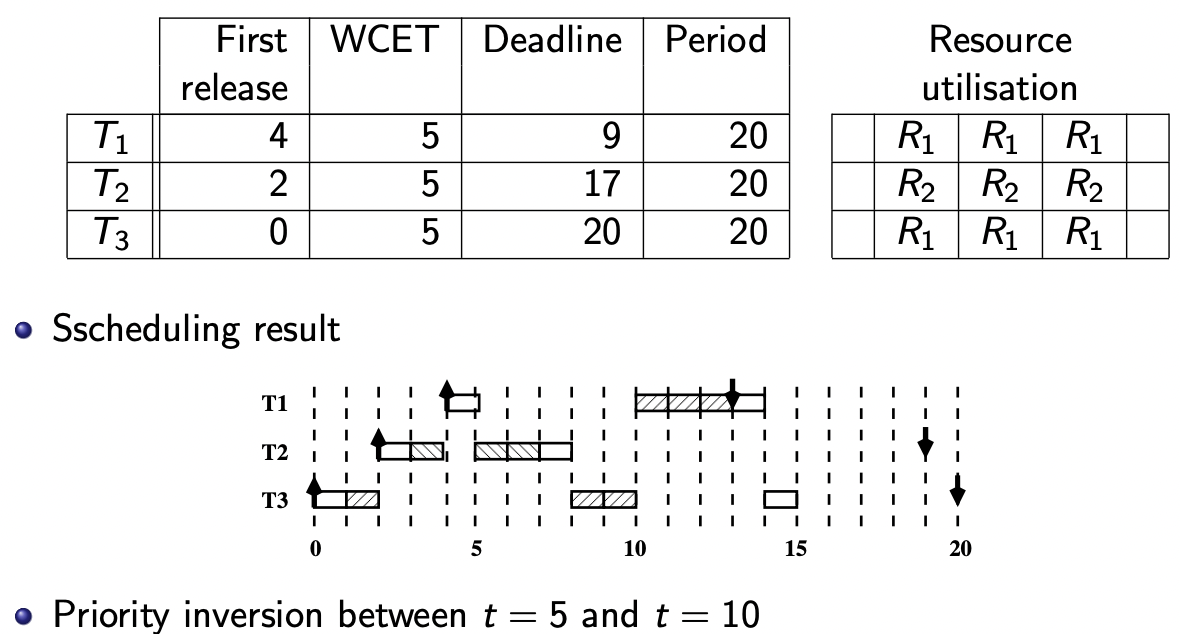
优先级倒置
优先级反转无法避免,但应该被限制资源等待时间(依托于资源分配机制)
【优先级倒置例子】
那么我们如何“避免”这些问题呢?
“超级优先级”(Super priority)方法是最简单的
方法描述:
当一个任务请求一个临界区资源时,会立即获得该资源。此时,该临界区拥有最高的优先级 任务在访问临界区资源时不会被抢占
在这种方法下:
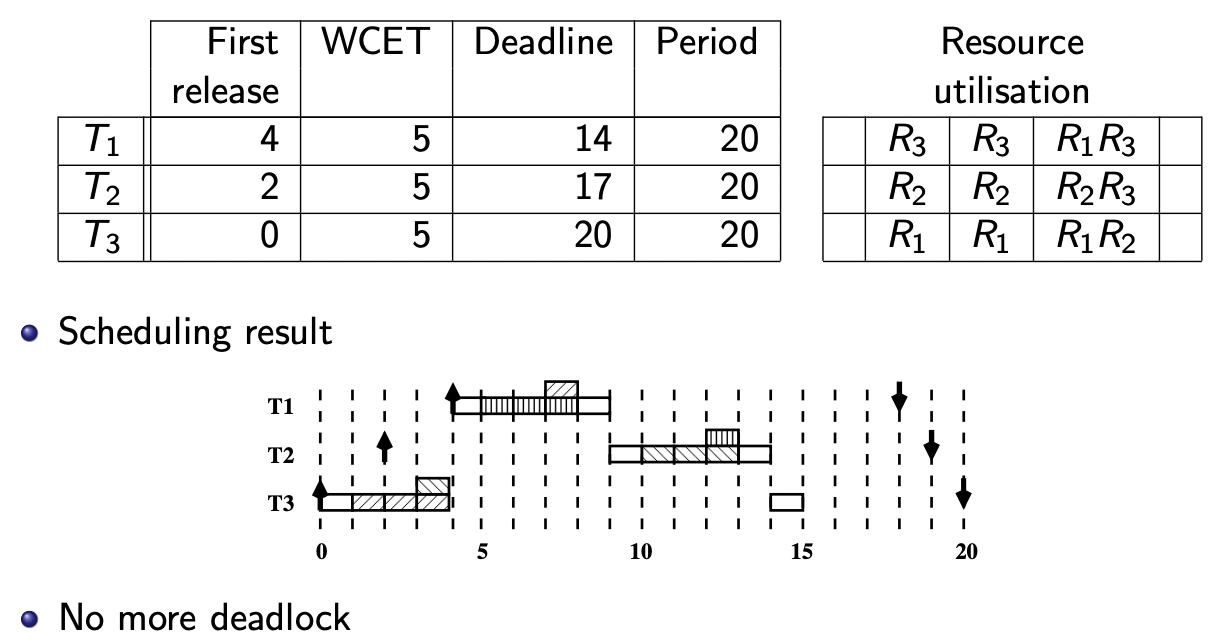
不会发生死锁
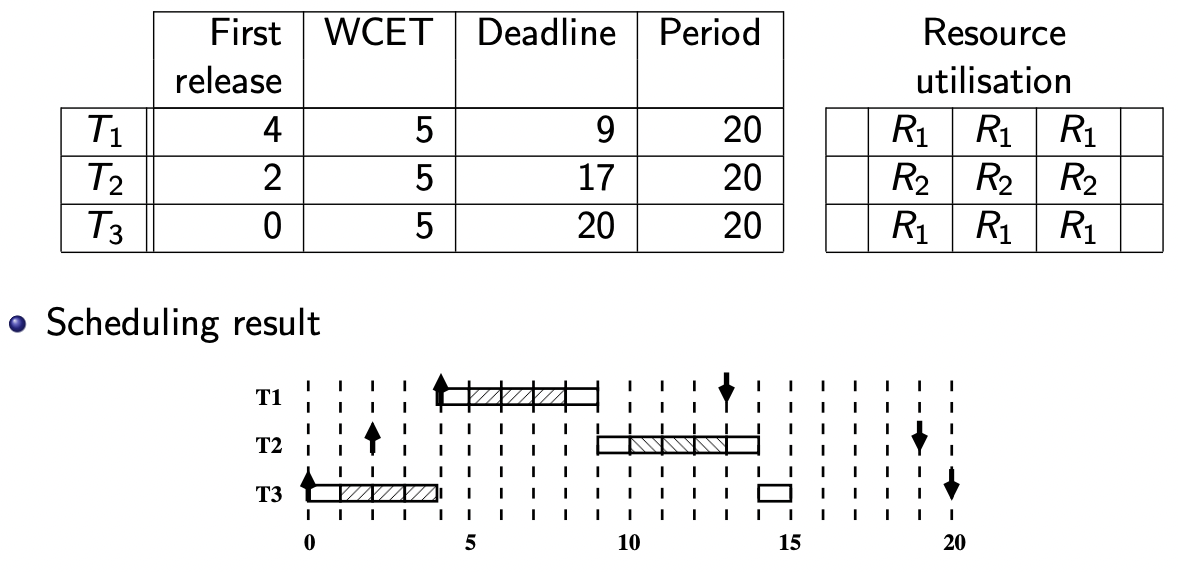
优先级反转的持续时间上限为最长临界区
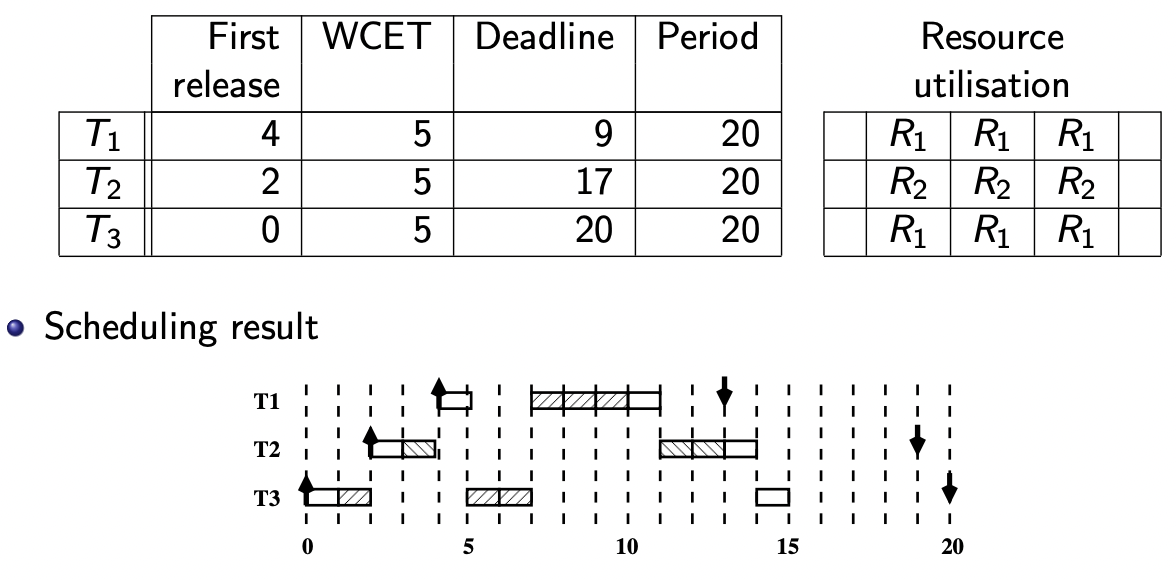
【例 1(课件 P 66 P_{66} P 6 6
【例 2(课件 P 67 P_{67} P 6 7
优先级继承(Priority inheritance)方法:不防止死锁 优先级反转的等待时间的上限被缩短
方法描述:
当高优先级任务 T h p T_{hp} T h p T l p T_{lp} T l p T l p T_{lp} T l p T h p T_{hp} T h p T l p T_{lp} T l p
之后恢复至原有的优先级
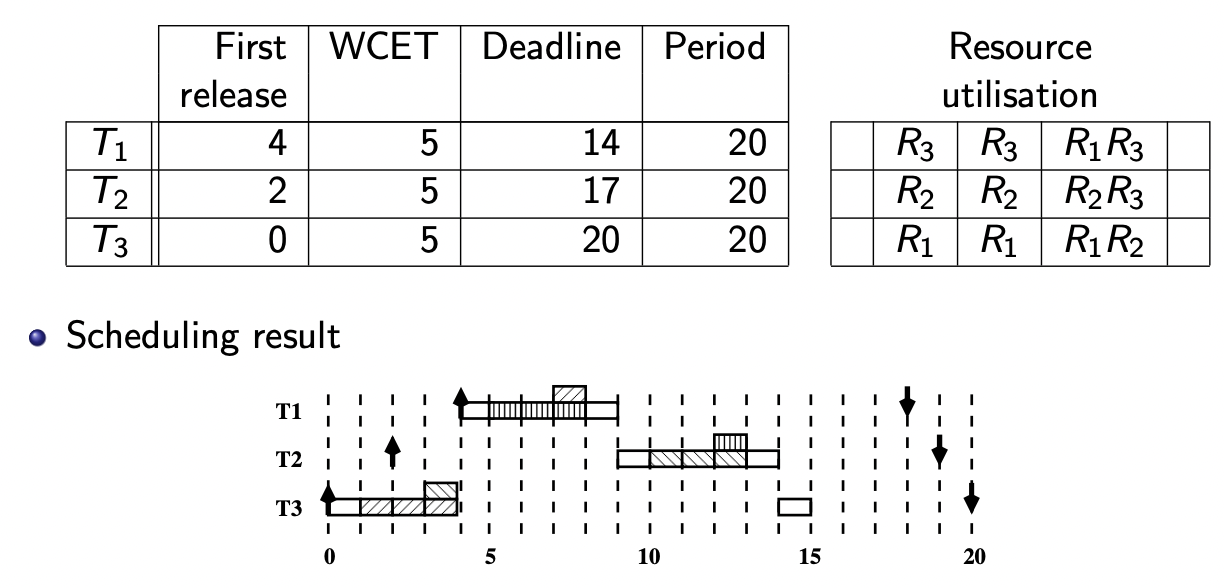
【例子(课件 P 70 P_{70} P 7 0
在这种方法中,每个临界区资源 堆栈 任务优先级 低 先入栈 高 后入栈
方法描述:
在开始之前,确定每个临界区资源的任务堆栈。
开始后,对于每个申请访问临界区资源
直到该任务退出临界区
【例子(课件 P 72 − P 74 P_{72} - P_{74} P 7 2 − P 7 4
在 m m m P P P T T T
每个处理器 P i P_i P i 最多执行一个任务 T j T_j T j
每个任务 T j T_j T j 最多由一个处理器 P i P_i P i
对于多处理器的调度,我们主要将其分为两个部分:分区调度 全局调度
无迁移的分区调度 任务级别迁移的全局调度 工作 Job 级别迁移的全局调度
对于分区调度,我们将任务静态地分布在可用的处理器上(类似于装箱问题)。
对于每个处理器来讲,它使用之前介绍的单处理器调度方法来独立执行