分布式系统与算法 - 课程笔记
写在前面:
本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第九学期课程 “Systèmes et algorithmes répartis” 及以下参考资料总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考资料:
- 《Systèmes et algorithmes répartis》Philippe Quéinnec, Gérard Padiou
- 《分布式计算——原理、算法与系统》 Kshemekalyani, A. D. and Singhal, M.
- 《分布式系统概念与设计》第5版
- 逻辑时钟-如何刻画分布式中的事件顺序
- 周刊(第22期):图解一致性模型 - codedump’s blog
- YOUTUBE : CSE138 (Distributed Systems) lectures, Spring 2021
零、概述
我们把分布式系统定义成一个其硬件或软件组件分布在联网的计算机上,组件之间通过传递消息进行通信和动作协调的系统。这个简单的定义覆盖了所有可有效部署连网计算机的系统。由一个网络连接的计算机可能在空间上的距离不等。我们定义的分布式系统有如下特征:
- 并发:在一个计算机网络中,执行并发程序是常见的行为。用户可以在各自的计算机上工作,在必要时共享诸如 Web 页面或文件之类的资源。系统处理共享资源的能力会随着网络资源 (例如,计算机)的增加而提高。对共享资源的并发执行程序的协调也是一个重要和重复提及的主题。
- 缺乏全局时钟 :在程序需要协作时,它们通过交换消息来协调它们的动作。密切的协作通常取决于对程序动作发生的时间的共识。但是,事实证明,网络上的计算机与时钟同步所达到的准确性是有限的,即没有一个正确时间的全局概念。这是通信仅仅是通过网络发送消息这个事实带来的直接结果。 定时问题和它们的解决方案将在下一章描述。
- 故障独立性:所有的计算机系统都可能出故障,一般由系统设计者负责为可能的故障设计结果。 分布式系统可能以新的方式出现故障。网络故障导致网上互连的计算机的隔离,但这并不意味着它们 停止运行,事实上,计算机上的程序不能 检测到网络是出现故障还是网络运行得比通常慢。类似的, 计算机的故障或系统中程序的异常终止(崩溃),并不能马上使与它通信的其他组件了解。系统的每个组件会单独地出现故障,而其他组件还在运行。
构造和使用分布式系统的主要动力来源于对共享资源的期望。“资源” 一词是相当抽象的,它涉及的范围从硬件(如硬盘、打印机)到软件定义的实体 (如文件、数据库和所有的数据对象) 等。
随着分布式系统的应用范围和规模的扩展,可能会遇到许多如下的挑战:
- 异构性:分布式系统必领由多种不同的网络、操作系统、计算机硬件和编程语言构成。互联网通信协议屏蔽了网络的差异,中间件能处理其他的差异。
- 开放性:计算机系统的开放性是决定系统能否以不同的方式被扩展和重新实现的特征。分布式系统应该是可扩展的——第一步是发布组件的接口,但由不同程序员编写的组件 的集成是一个真正的挑战
- 安全性:分布式系统中维护和使用的众多信息资源对用户具有很高的内在价值,因此它们的安全相当重要。 信息资源的安全性包括 三个部分:机密性 (防止泄露给末授权的个人)、完整性 (防止被改变或被破坏)、可用性 (防止对访问资源的手段的干扰)。
- 可伸缩性:分布式系统可在不同的规模 (从小型企业内部网到互联网)下有效且高效地运转。如果资源数量和用户数量激增,系统们能保持其有效性,那么该系统就称为可伸缩的。
- 故障处理:计算机系统有时会出现故障。分布式系统的故障是部分的,也就是说,有些组件出了故障而有些组件运行正常。因此故障的处 理相当困难。我们将讨论下列处理故障的技术:
- 检测故障:有些故障能被检测到。例如,校验和可用于检测消息或文件中出错的数据。
- 掩盖故障:有些被检测到的故障能被隐藏起来或降低它的严重程度。例如:消息在不能到达时进行重传;将文件数据写入两个磁盘,如果一个磁盘损坏,那么另一个磁盘的数据仍是正确的(冗余)。
- 容错:互联网上的大多数服务确实有可能发生故障,试图检测并隐藏在这样大的网络、这么多的 组件中发生的所有故障是不太实际的。服务的客户能被设计成容错的,这通常也站及用户要容忍错误。 例如,当 Web 浏览器不能与 Web 服务器连接时,它不会让用户一直等待它与服务器建立连接,而是通知用户这个问题,让用户自由选择是否尝试稍后再连接。
- 故障恢复:恢复涉及软件的设计,以便在服务器崩溃后,永久数据的状态能被恢复或 “回滚”。
- 并发性:在分布式系统中,服务和应用均提供可被客户共享的资源。因此,可能有几个客户同时试图访向一个共享资源的情况。所有资源必须被设计成在并发环境中是安全的。
- 透明性:透明性被定义成对用户和应用程序员屏蔽分布式系统的组件的分离性,使系统被认为是一个整体, 而不是独立组件的集合。访问透明性、位置透明性、兵法透明性、复制透明性、故障透明性、移动透明性、性能透明性和伸缩透明性。
- 服务质量:在分布式系统中仅提供对服务的访问是不够的。特别是,提供与服务访问相关的质量保障也是重要的。这种质量的例子包括与性能、安全性和可靠性相关的参数。
一、时间与全局状态
本章将重点介绍分布式系统中与时间有关的问题。时间是理解分布式运行的一个重要的理论概念。每台计算机都有自己的物理时钟,但是不同计算机件的物理时钟存在偏离,我们无法将他们精确同步。而对于全局物理时间的缺乏,使得我们无法知道各个分布式程序在运行中的状态,例如对于一个分布式进程A 来讲,它并不知道另一个分布式进程 B 的状态。但是对于确实需要观察分布式系统,确定事件的某些状态是否会同时出现。此时我们引入逻辑时间与逻辑时钟(物理时钟任然有许多同步算法,恕在此不做讨论)。
0 全局物理时钟
对于上面提到的两个问题,我们试图解决的一个天然想法是, 记录每个分布式进程中发生事件的原始时间戳, 并把它连同事件本身扩散到其他节点,这样其他节点的视角上就可以观察到完整的因果顺序了?
If you have one clock, you know what the time is. If you have two, you are not sure.
大家都清楚的一点是,不同节点的物理时钟其实是不一致的,而且无法做到精确一致。
其原因:
- 仍然是由于网络延迟的不确定,我们无法通过网络同步时间来获取一个全局一致的物理时钟。
- 现实中的多个时钟,即使时间已经调成一致,但是由于日积月累的计时速率的差异,会导致时钟漂移而显示不同的时间。
如此看来,寄希望于一个全局的时钟来对事件顺序做全局标定也是不现实的。
参考链接:
1 逻辑时间与逻辑时钟
逻辑时钟的概念是由著名的分布式系统科学家 Leslie Lamport 提出, 在他的那篇著名的论文《Time, Clocks and the Ordering of Events in a Distributed System》的介绍上,lamport提到了著名的狭义相对论:
Special relativity teaches us that there is no invariant total ordering of events in space-time; different observers can disagree about which of two events happened first. There is only a partial order in which an event precedes an event iff can causally affect .
爱因斯坦的狭义相对论告诉我们,时空中不存在绝对的全序事件顺序, 不同的观察者可能对哪个事件是先发生的无法达成一致。 但是有偏序关系存在,当事件 是由事件 引起的时候, 和 之间才有先后关系。
一个简单的例子:“假如太阳消失了(事件 A),地球上的我们(观察者)也要在8分钟之后感知到太阳消失了。”
也就是说,一个事件 A 发生后, 载有这个事件信息的光(引力、无论什么,快不过光速)到达观察者之前, 观察者是无法没有任何感知的, 这时我们就无法定义事件的顺序。 而当信息最终传播到达观察者时, 这个事件也就对观察者发生了影响, 造成了一个新的事件 B,叫做“观察到了事件 A 的事件 B”。 这时我们才有 A happened before B 的因果关系。
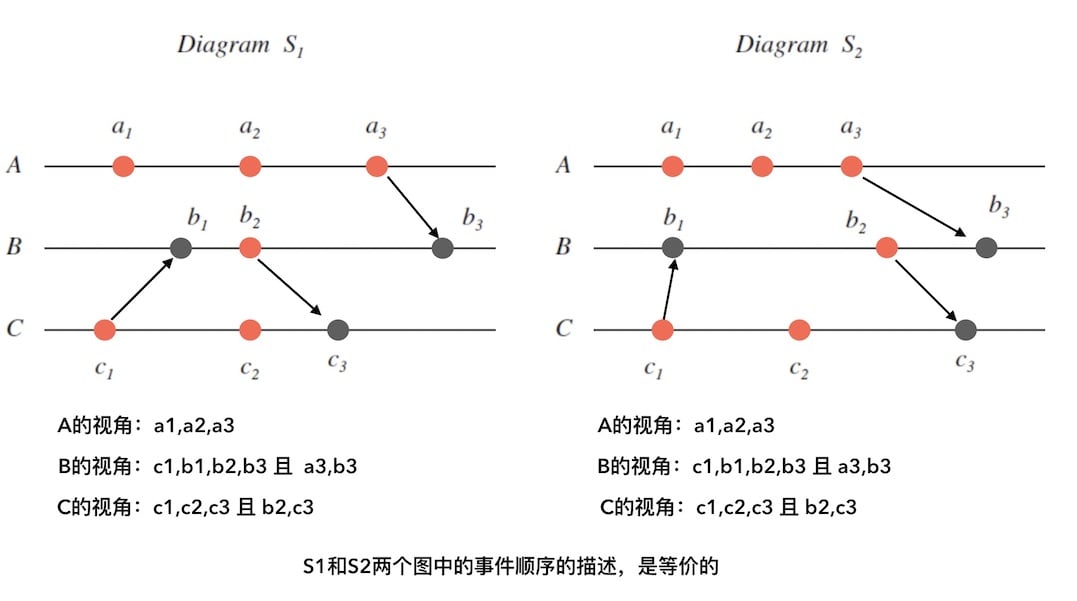
而这种对于描述事件顺序的“happened before”,在进程的视角下依然成立。如下图
因果关系
通常,我们使用类似物理因果关系 (Relation de causalité) 的方案,但将它应用到分布式系统是为了给发生在不同进程里的事件排序。这种排序是基于下面既简单又直观的几点:
-
如果两个事件发生在同一个进程 中,那么他们发生的顺序是 观察到的顺序,即
-
当一条消息在不同的进程之间发送时,发送消息的事件在接受消息的事件之前发生。即
-
这种发生在先的因果序存在传递性。即
-
但是并不是所有的事件都可以按照以上的规则推断出明确的先后顺序,此时我们说这两个事件是并发的。即
【例 1】在如下这个例子中,我们可以找出各个事件间的逻辑时间先后关系:
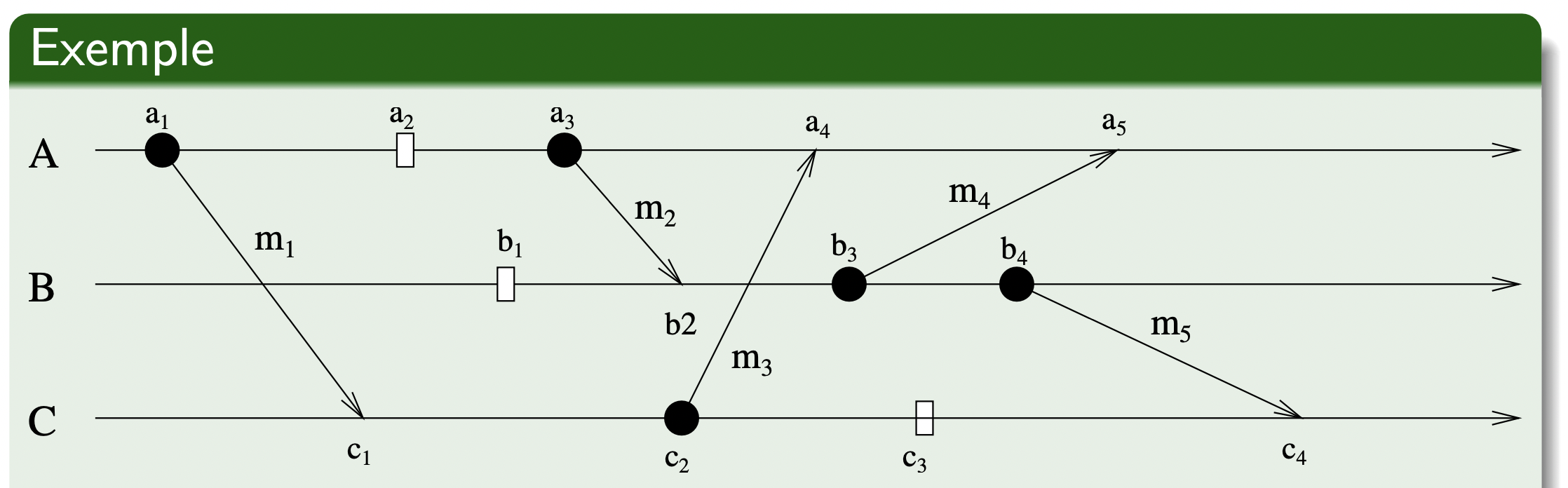
- 且 且
past() 与 future() 因果集
前面我们已经学习了事件之间的因果关系。那么对于一个事件 ,如果:
-
明确其他事件先于事件 发生,那么我们可以将其归为一个
past(e)的集合。即 -
相反,如果事件 先于其他事件发生,则归为
future(e)集合。即 -
其余的事件归为
concurrence(e)集合:
如下图,是一个 PAST 集合为分割线 passé(b2) 左侧所有事件组成,FUTURE 集合则为分割线 futur(b2) 右侧所有事件组成:
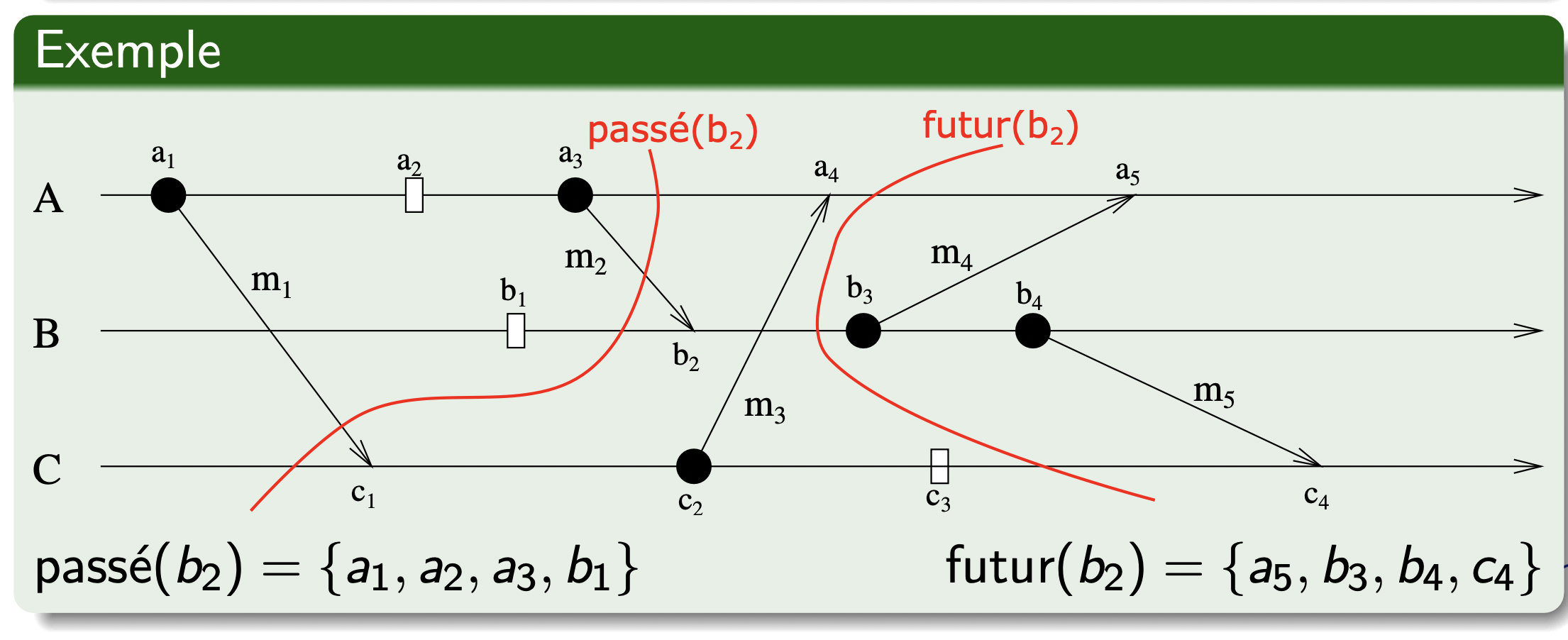
逻辑时钟
现在,我们开始讨论 Lamport 的逻辑时钟算法。首先我们需要明确一点: 逻辑时钟并不度量时间本身,仅区分事件发生的前后顺序。
从单个进程的⻆度看,事件可唯一地按照本地时钟显示的时间进行排序。但 Lamport [1978] 指 出,因为我们不能在一个分布式系统上完美地同步时钟,因此通常我们不能使用物理时间指出在分布式系统中发生的任何一对事件的顺序。
Lamport 逻辑时钟
Lamport 逻辑时钟是 一个单调增长的计数器 ,它的值与任何物理时钟无关。
对于每个进程 ,维护它自己的逻辑时钟 ,进程用它给事件加上时间戳 (Lamport timestamp)。我们用 表示 的事件 的时间戳,用 表示发生在任一进程中的事件 的时间戳。
Lamport 的时钟算法:
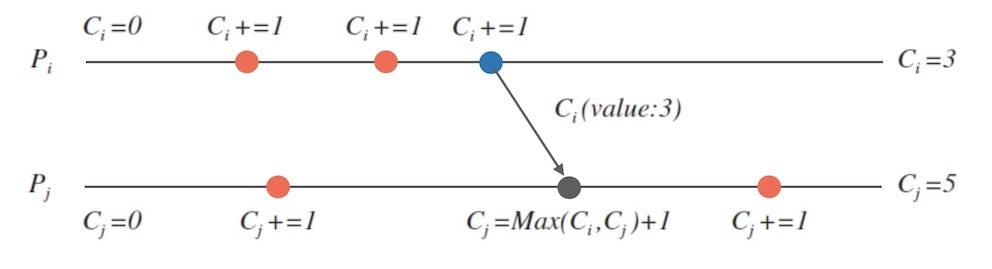
- 每个进程 内维护本地一个计数器 ,初始为 ;
- 每次执行一个事件 ,计数器 自增 (假设自增量为 );
- 进程 发消息 给进程 时,需要在消息上附带自己的计数器 ;
- 当进程 接收 消息时,更新自己的计数器 。
通过与事件 与事件 有关的事件序列上进行长度归纳,我们可以很容易地得出:
但是相反的情况是不成立的。如果 ,我们不能推导出 。例如【例1】中, ,但是 ,我们不能推导出 。
Lamport 的逻辑时钟算法构建了一个全序 (total ordering) 时钟来描述事件顺序, 但是我们知道“happened before”是一个偏序关系, 用全序关系的一维计数器来描述“happened before” 的话, 就会导致无法等价化描述的结果, lamport时钟的缺陷在于:如果两个事件并不相关,那么这个时钟给出的大小关系则没有意义, 这个缺陷其实恰好就是全序和偏序的不同点而已。
所以,要准确描述事件顺序,我们终究要寻求偏序方法。于是,我们继续探讨向量时钟。
向量时钟
Matter [1989] 和 Fidge [ 1991] 开发了向量时钟用以克服 Lamport 时钟的缺点:我们 ,不能推导出 。有 个进程的系统的向量时钟是 个整数的一个数组。每个进程维护它自己的向量时钟 ,用于给本地事件加时间戳。与 Lamaport 时间戳 类似,进程在发送给对方的消息上附加向量时间戳,更新时钟的规则如下:
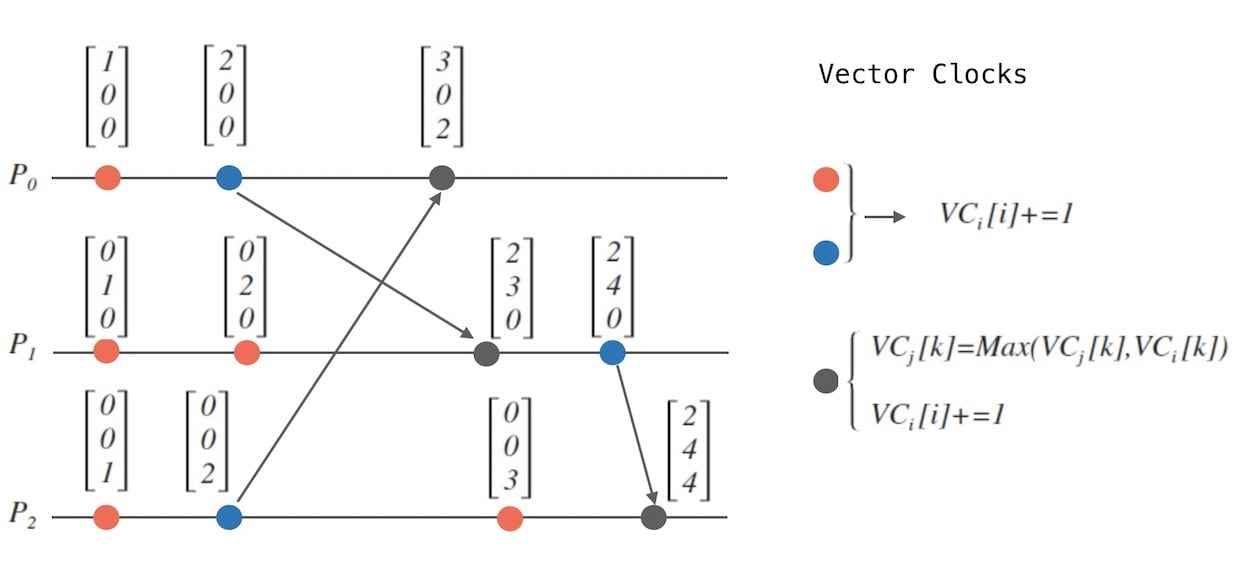
- 初始化各个进程 的向量, 全部置为 :。
- 进程 每发生一个事件时, 其向量的第 个元素自增: 。
- 当进程 发消息给进程 时,需要在消息上附带自己的向量 。
- 当进程 接收到消息时,合并对方的时钟,并在自己的时钟上自增:
- 对 上的任意一个整数 执行
- 接着,对应第 2 点:
与 Lamport 的异同
可以发现,向量时钟和 Lamport 的时钟算法结构一样, 不同的点在于:
- Lamport时钟只是在对齐时钟的计数器
- 而向量时钟是在对齐各自对整个系统的视角,其中包含各个进程内的时间戳。
向量时钟的性质
我们可以推导出来关于向量时钟比较大小的几个性质:
-
向量的各维相等,则向量相等。 这个是显而易见的。
-
向量时钟是有序的 (充要), 的各维上的值 对应维上的值, 则认为 。
-
向量时钟有序性质的进一步细化,定义了严格小于:如果 , 并且至少存在一个维,在这个维上 的值严格 在这个维上的值, 则认为 。
-
如果两个向量不存在大小关系,则认为两个向量平行,记作 。
这几个性质看起来复杂,其实都是在定义向量时钟之间的大小关系。 我们可以得出一个结论:
向量时钟之间的大小关系是一种偏序关系。
我们省去证明步骤,在此直接给出如下的结论:
-
向量有序,则事件有序(充要):
-
向量平行,则事件并发(充要):
向量时钟可以准确刻画事件顺序,其本质在于将 Lamport 时钟的全序计数器的方式改造成向量时钟的偏序大小关系。
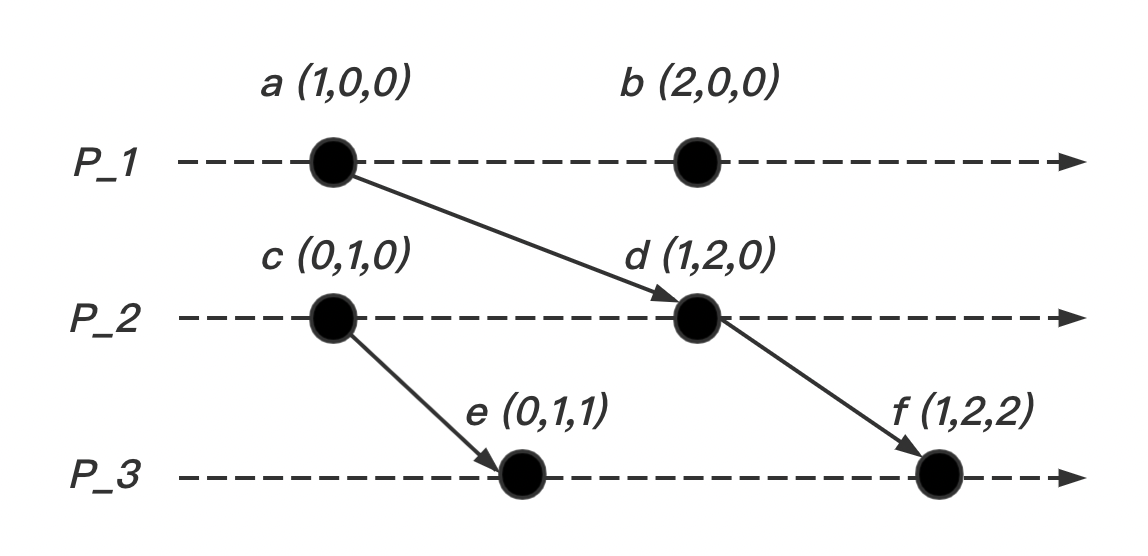
如下图所示,我们可以根据每个事件(图中点)的向量信息推导出事件的先后顺序为:
- ,
- ,
2 全局状态和一致割集
全局状态
从原理上说,观察单个进程的的连续状态是可能的,但是整个分布式系统的全局状态是十分困难的。其本质原因是缺乏全局时间。
如果所有进程都有完全同步的时钟,那么我们可以在同一时间让每个进程记录下它的状态,也就是系统实际的全局状态。从进程状态集中我们可以判断进程是否发生死锁等。但我们不能获得完美的时钟同步,所以这个方法不适用。
然而,在满足一定条件的情况下,利用不同时间记录的本地状态可以得出一个有意义的全局状态。
在一个有 个进程 的分布式系统中,如果一个进程 中发生了一系列事件,我们可以通过这个进程的历史来描述每个进程的执行过程:
理论上我们可以记录在这个进程 发生的事件,以及它经过的连续状态。我们用 来表示进程 在第 个事件 发生之前的状态,所以 是进程 的初始状态。我们注意到,在不同进程间发送、接收 消息 时,可以根据进程经过的连续状态记录发送 与接收 的状态。
解释 💡:什么是“根据进程经过的连续状态记录发送 与接收 的状态”?
我们以一张图作为讲解范例:
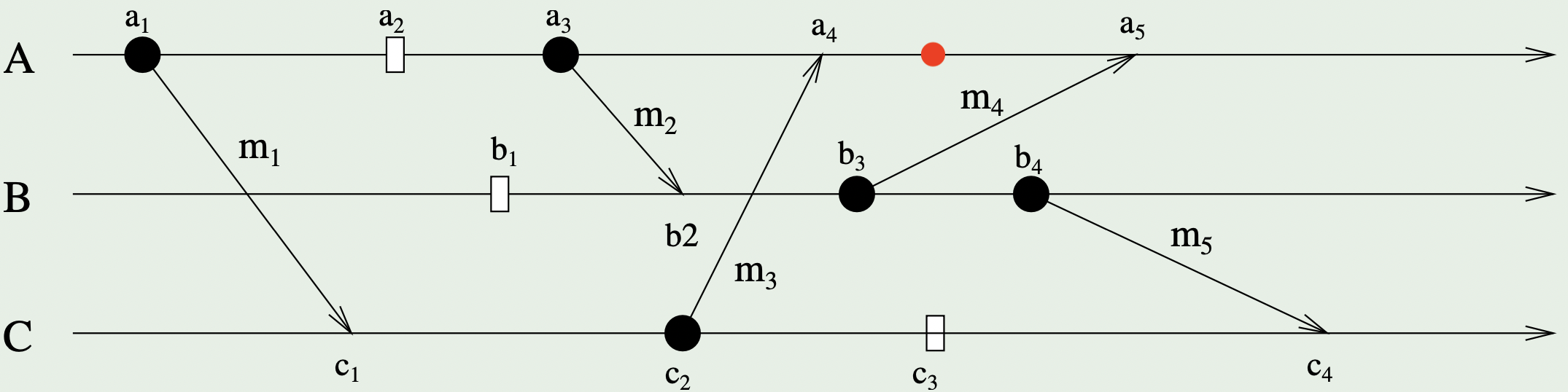
我们讨论进程 在事件 发生之前,即图中红点位置处的状态 :该进程
- 在事件 中发送 了消息 到另一个进程 ;
- 发生过事件 ;
- 在事件 中发送 了消息 到另一个进程 ;
- 在事件 中从另一个进程 接收 到消息 。
如果我们发现进程 已经发送 了一个消息 到另一个进程 ,那么通过检查 是否接收 到该消息 ,我们就能够推断出消息 是否是进程 和进程 之间信道状态的一部分。
通过取单个进程历史的并集,我们可以得到系统的全局历史 (global history):
理论上讲,我们可以取每个进程 上的任意状态组成集合,形成一个全局状态 。割集(Cut)是一种“有意义的”全局状态,是系统全局历史的子集,是进程历史前缀的并集。
在对应于割集 的全局状态 中的状态 是在由进程 处理的最后一个事件 之后的 状态。事件集 称为割集的边界(Frontier)。
一致性割集
在如下所示的图中给出了进程 , 和 中发生的事件。该图给出了两个割集(红色部分)。
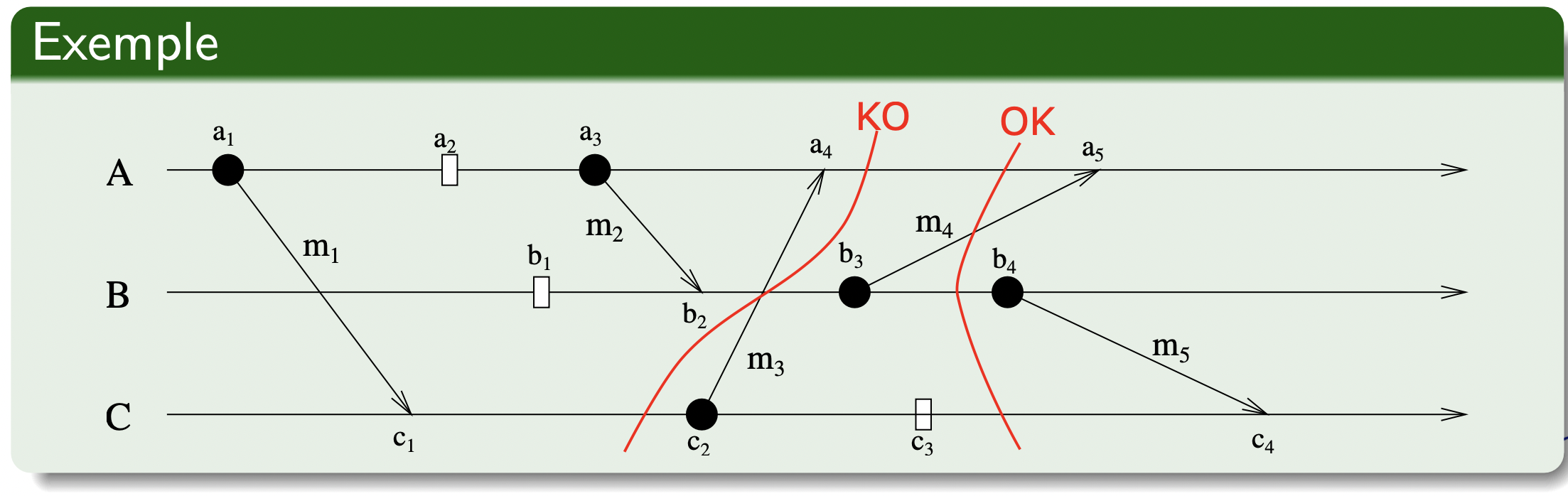
一个割集的边界是 ,另一个割集的边界是 。
-
最左割集是不一致(inconsistent)的。这是因为在进程 的事件 它包含了对消息 的接收,但在其他进程中不包含对该消息的发送。这是一个没有原因的结果。 实际的执行不会处于该割集边界所对应的全局状态。
-
相反,最右割集是一致(consistent, cohérentes)的。它包括消息 、 和 的发送和接收。它也包括消息 的发送但不包括 的接收。这与实际执行相一致,毕竟,消息要花一些时间才能到达。有因必有果或有因(一段时间后总会有果)。
网格
至此,我们已经知道了如何判定一个割集(全局状态)是否是一致的。在分布式系统内,我们希望获得一致性的全局状态,以便在后续能在系统当中实现互斥、同步等管理。那么我们又该如何更直观的得到“有意义的”全局状态(所有的一致性割集)呢?我们引入网格(Treillis)的概念:
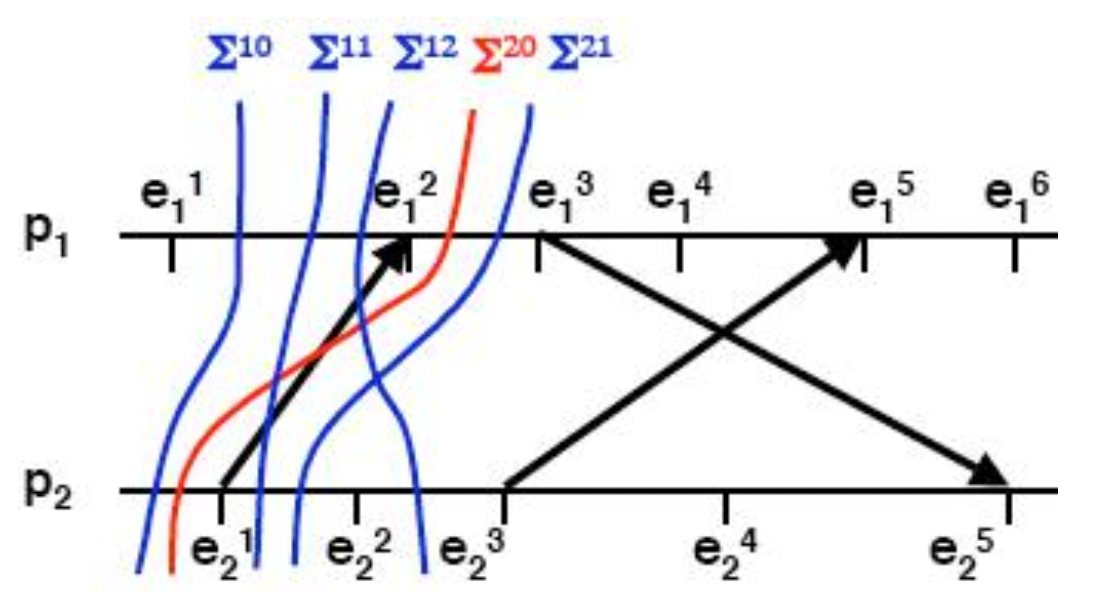
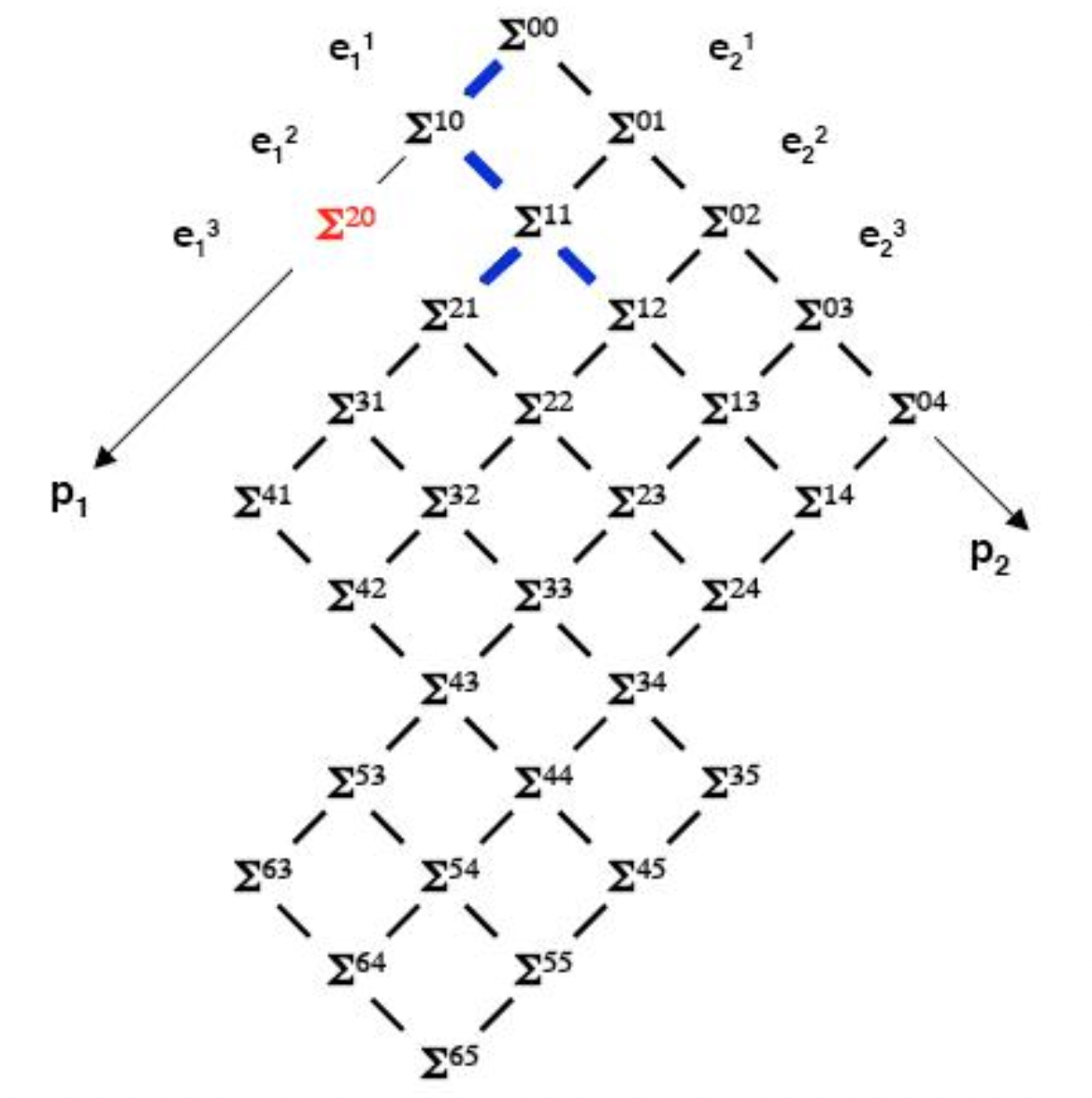
我们考虑如图所示的进程执行情况,我们可以找出这个分布式系统中所有的一致性割集,并将其以网格图像的形式表现出来。其中:
- 坐标系:各个进程 发生的事件 ;
- 节点 :对应一个关于 和 一致性割集(全局状态);
- 节点间的“路径”:两个一致性割集(全局状态)间的连线。
快照(Snapshots, Cliché)算法
- 快照:所谓快照,就是记录系统中的所有进程 的全局状态(包括通道状态)。
- 分布式快照主要用途:故障恢复(即检查点)、死锁检测、垃圾收集等。
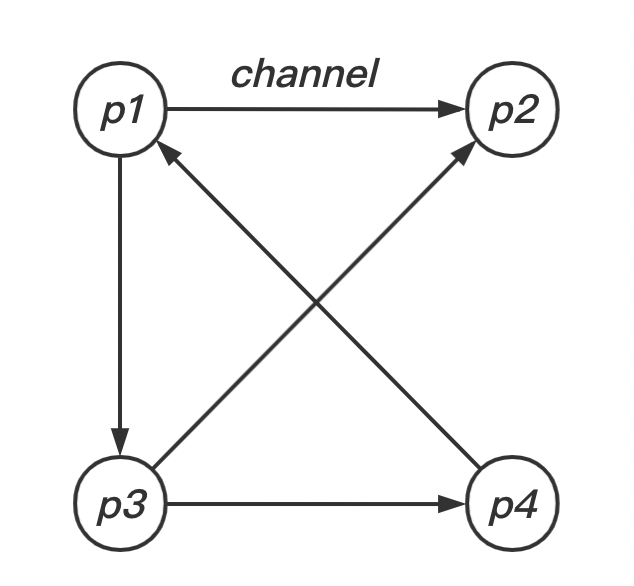
定义分布式系统的全局状态,我们先将分布式系统抽象成有限个进程和进程之间的通道(Channel)组成,也就是一个有向图(如上图):节点是进程,边是通道是分布式系统,也就是说,这些进程是运行在不同的物理机器上的。那么一个分布式系统的全局状态就是有进程的状态和通道中的消息组成,这个也是分布式快照算法需要记录的。
由于进程之间通过通道不停地交换数据,所以以下的动作都会造成进程状态的改变:
- 进程 收到或发出一条消息 ;
- 通道 内存在(承载)一条离开或到达进程 的消息 ;
那么我们如何得到这个系统内每个进程在某一“时刻”的状态呢?
在分布式的快照算法中,我们先假设:
- 系统中的任意两个节点之间都可以通过通道通信。发送消息的这一端被称为接入通道(Incoming Channel),接收消息的这一端成为外出通道(Outgoing Channel);
- 通道和进程都不会出现故障:通信是可靠的,每个发送的消息都会被完整地接收(TCP/IP 协议);
- 通道是单向的,提供 FIFO 顺序的消息传递;
- 在执行快照的过程中,进程可以继续原本的任务,发送接收消息。
我们在算法中使用了一种特殊的标记(Marker)消息。标记有双重作用:
- 如果接收者(Receiver)还没有保存自己的状态,那么该标记作为提示保存(Record)状态的提示;
- 如果接收者已经保存了自己的状态,该标记作为停止接入通道的消息流入的提示。
算法表述
1. 发起 (Initiating) 一个快照:
- 进程 发起: 记录自己的进程状态,同时生产一个标识信息
marker,marker和进程通信的 不同 - 将
marker信息通过 Outgoing channel 发送给系统里面的其他进程 - 开始记录所有 Incoming channel 接收到的
2. 传播 (Propagating) 这个快照:
对于进程 从 Incoming channel 接收到从进程 发送的 marker 信息:
-
如果 还没有记录自己的进程状态,则
- 记录自己的进程状态,同时将 Incoming channel 置空
- 向进程 的所有 Outgoing channel 发送
marker信息
-
否则
- 记录其他 Incoming channel 在收到
marker之前的通道中收到所有
- 记录其他 Incoming channel 在收到
所以这里的
marker其实是充当一个分隔符,分隔进程做 local snapshot (记录进程状态)的 。比如 做完 local snapshot 之后 中发送过来的 为[a,b,c,marker,x,y,z]那么a, b, c就是进程 做 local snapshot 前的数据, 对于这部分数据需要记录下来,比如记录在 log 里面。而marker后面 正常处理掉就可以了。
3. 停止 (Terminating) 快照算法
- 所有的进程都收到
marker信息并且记录下自己的状态和 channel 的状态(包含的 )
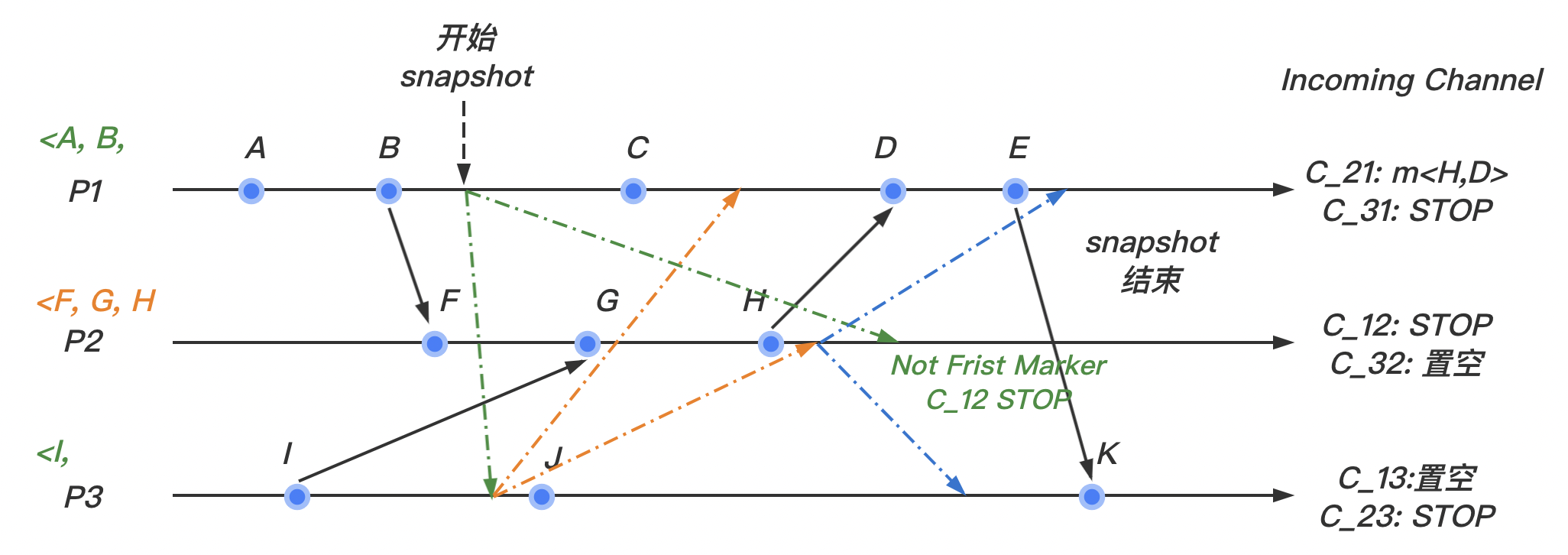
4. 时序图演示
(1)我们在 进程如图所示的地方开始快照算法
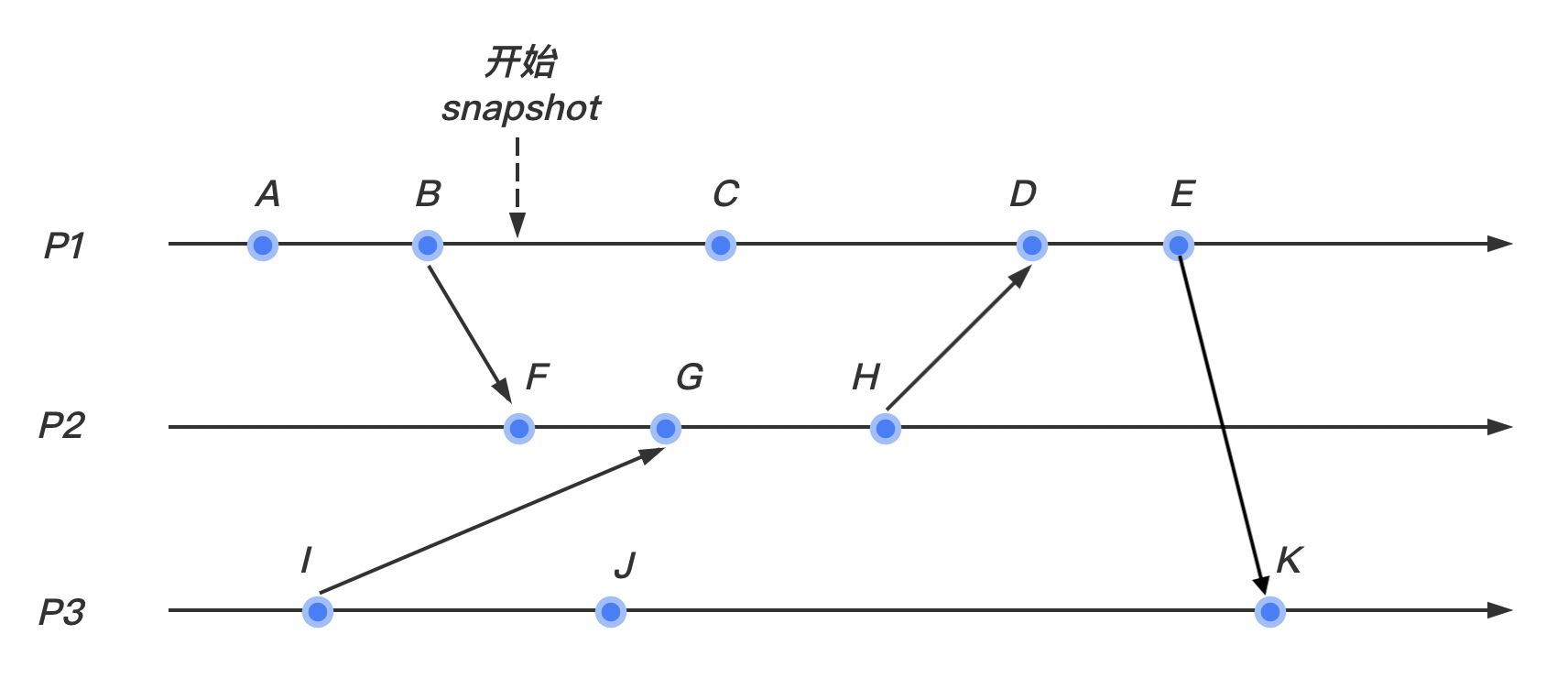
(2)我们假设 marker 标记在我们的系统内按照如图所示的情况在个进程间传递:
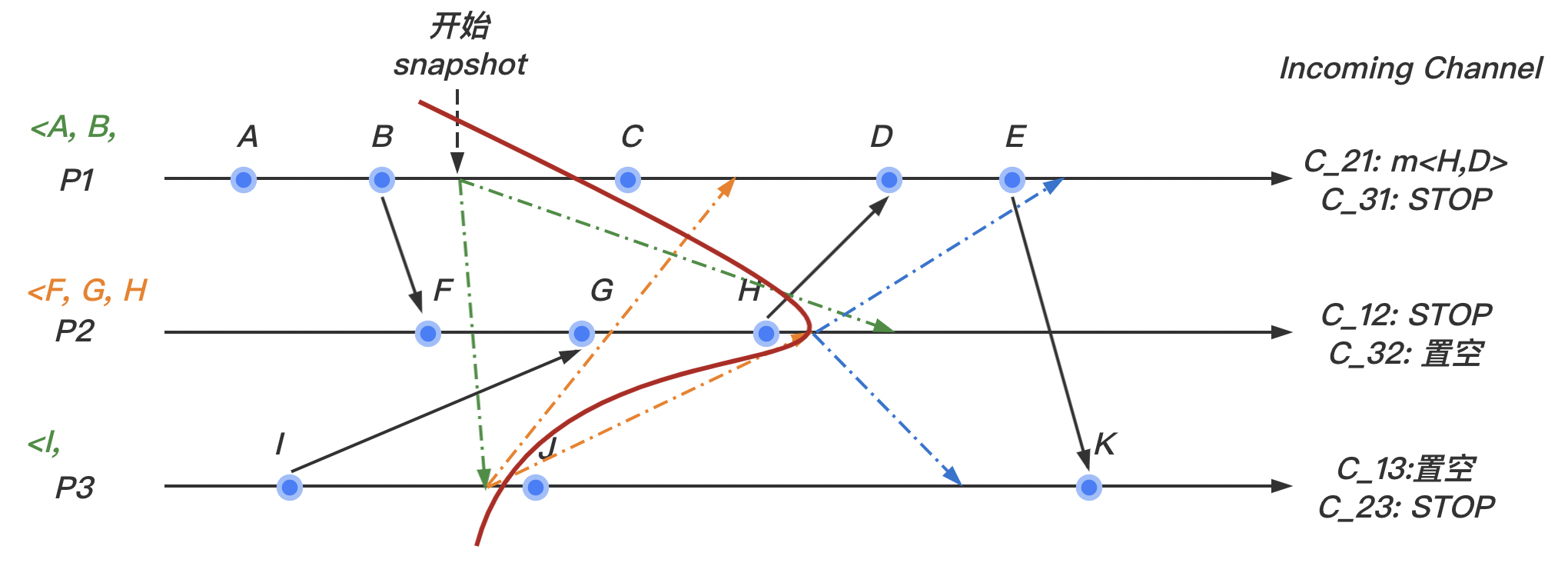
marker最先到达 进程。此时 进程并没有marker的记录,所以记录该进程的状态,然后将输入通道 置为空。继续向其他的通道发送marker。
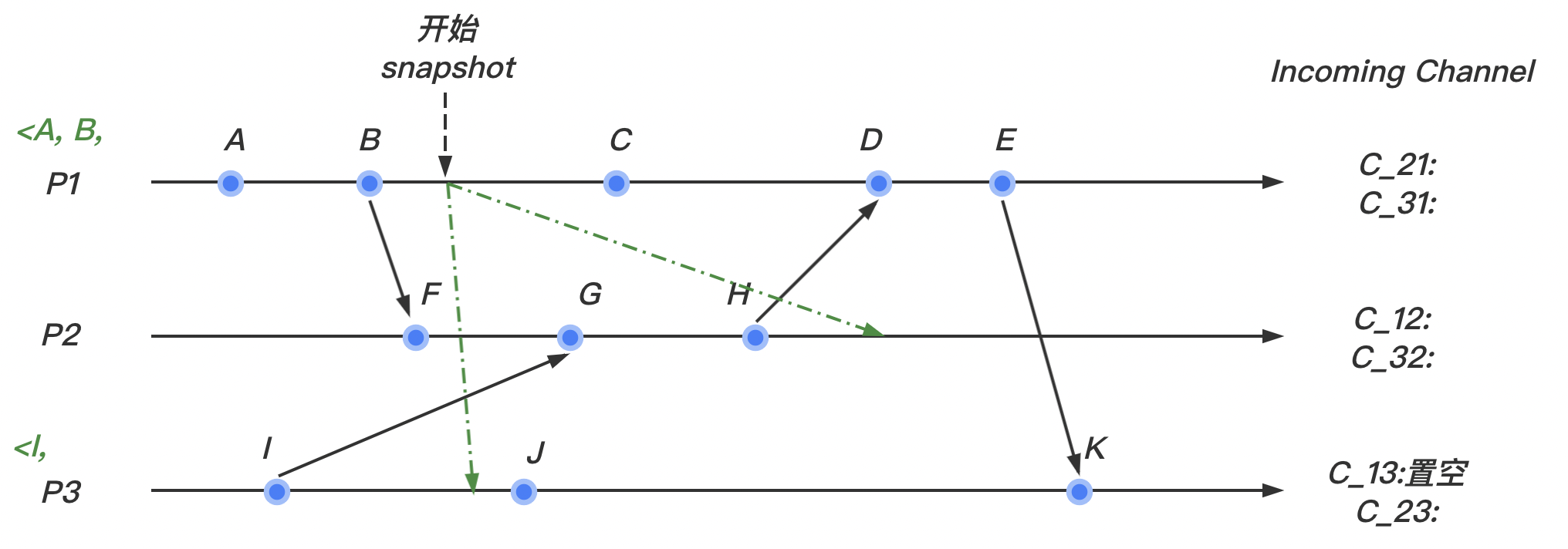
(3)
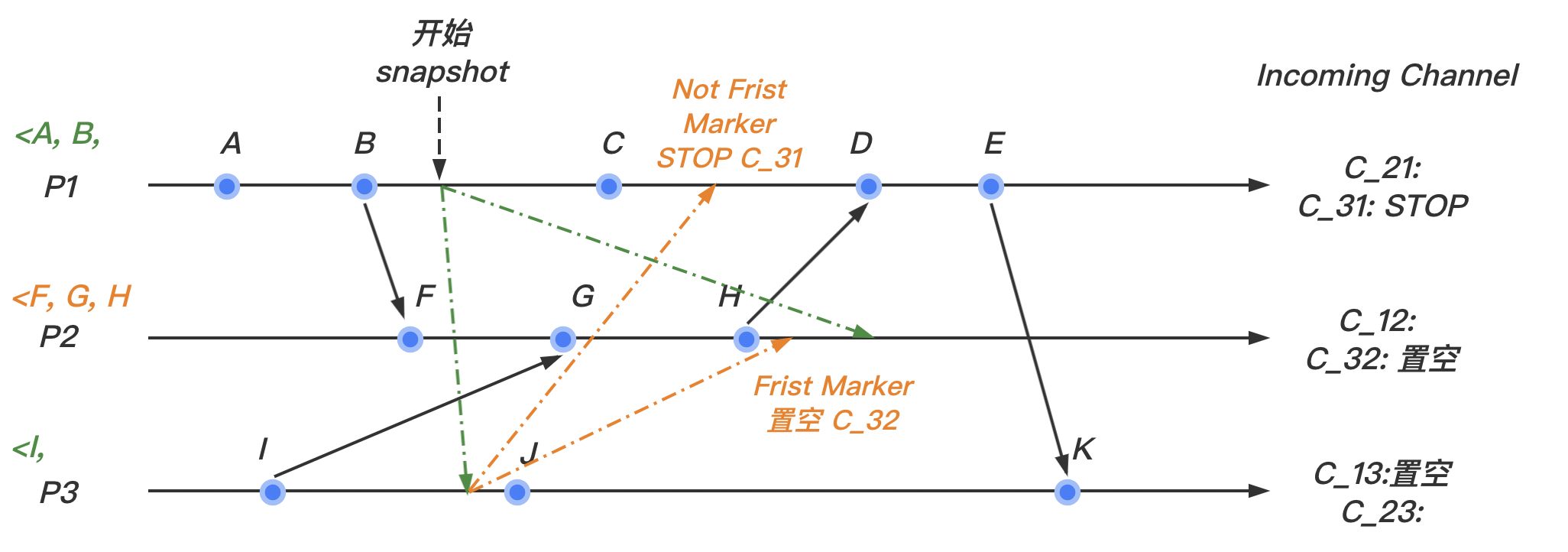
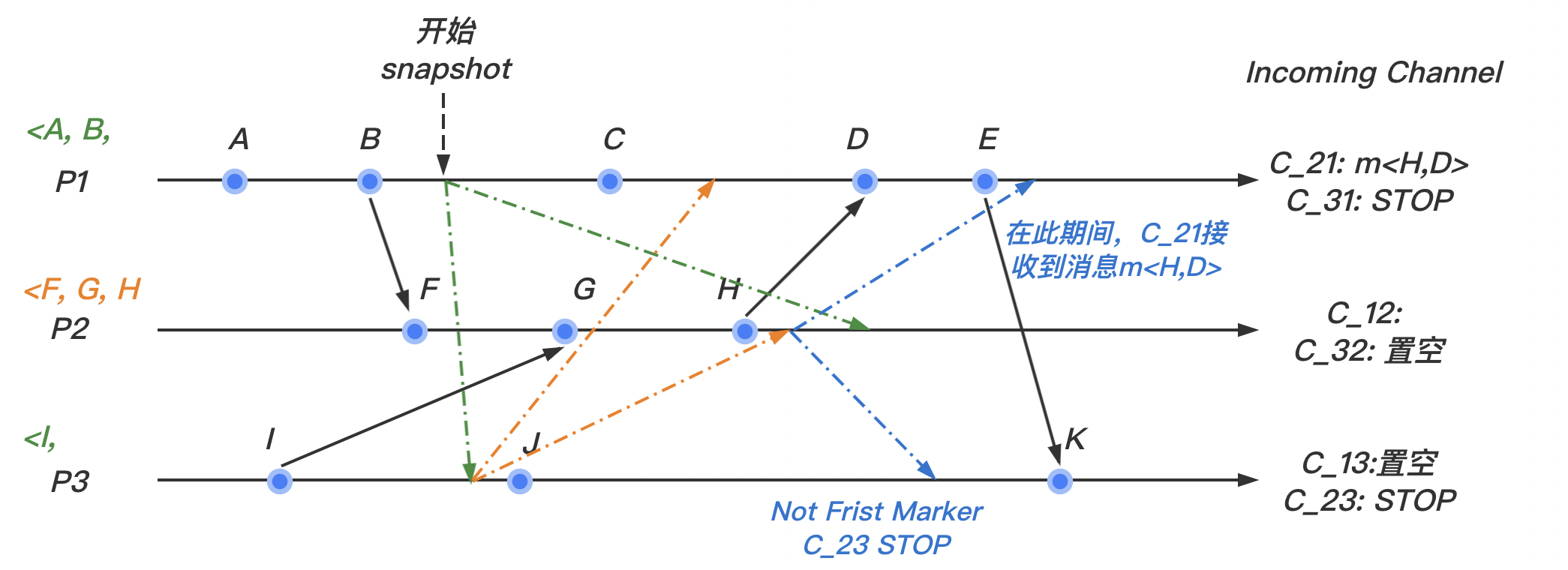
二、分布式互斥
https://www.bilibili.com/video/BV1KL4y1T7Wy/
互斥是分布式计算系统的一个基本问题。互斥确保多个进程对一个共享资源或数据的并发访问是顺序的,即以一种互斥的方式执行。消息传递是实现分布式互斥的唯一方法。其三种基本实现方式如下:
-
基于令牌(
token)的方式:在基于令牌的方法中,所有站点共享一个唯一的令牌。如果一个站点拥有这个令牌,则被允许进入临界区,直到临界区执行完成后这个站点才释放这个令牌。由于令牌的唯一性,互斥得以保证。
-
基于权限(Permission)申请方法:
-
集中式方法(中央服务算法)
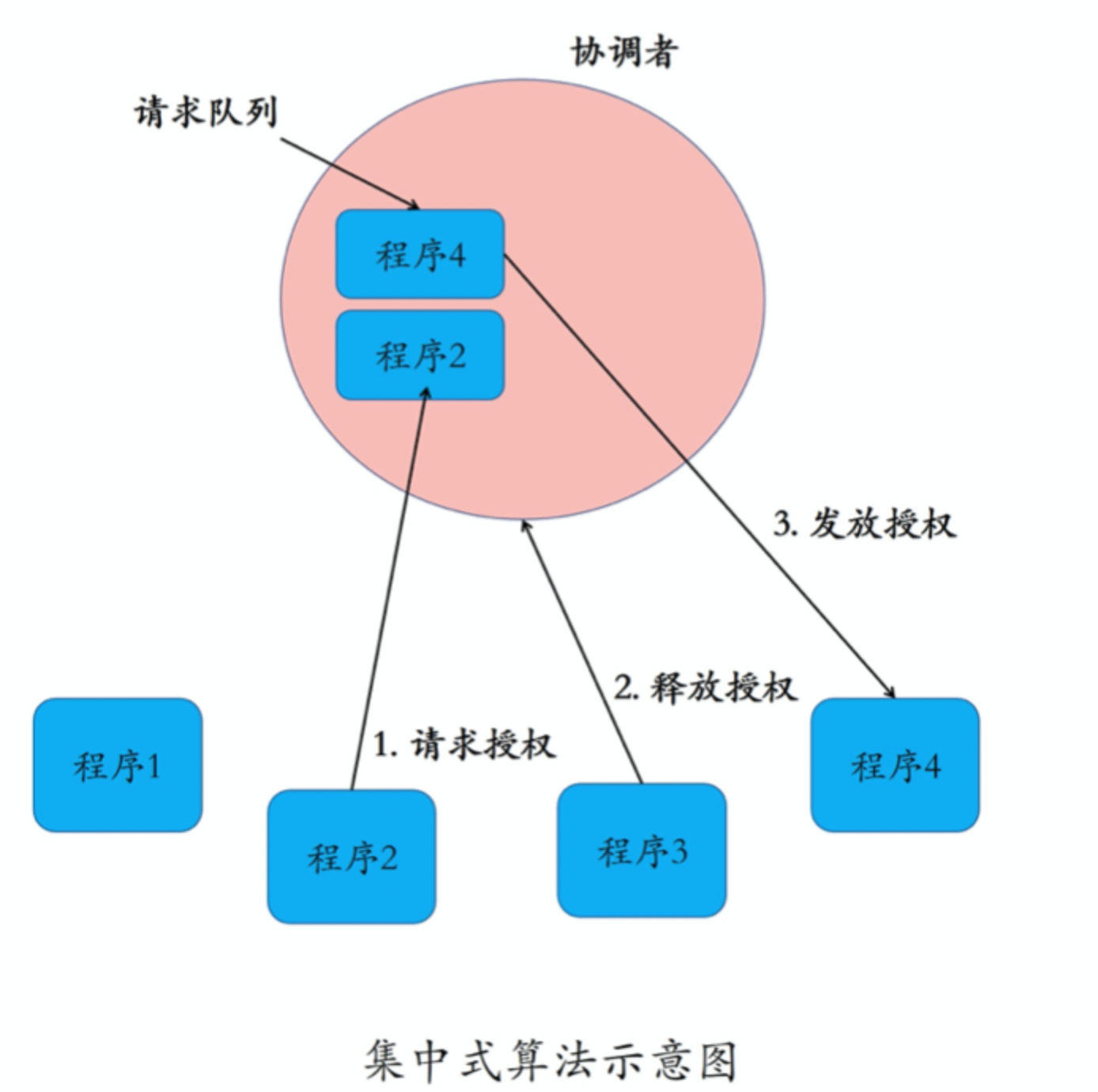
引入一个协调者进程,得到一个分布式互斥算法。每个程序在需要访问临界资源时,先给协调者发送一个请求。
如果当前没有程序使用这个资源,协调者直接授权请求程序访问;否则,按照先来后到的顺序为请求程序。
如果有程序使用完资源,则通知协调者,协调者从“排号”的队列里取出排在最前面的请求,并给它发送授权消息。
拿到授权消息的程序,可以直接去访问临界资源。每个程序完成一次临界资源访问,需要进行 3 次消息交互。
-
分布式方法 (使用组播和逻辑时钟的算法,如 Lamport 或 Ricart-Agrawala)
站点间通过传递两轮或更多轮的消息来决定哪个站点将进入临界区:当一个站点关于局部变量定义的断言的值变为真时,它就进入临界区。由于在任何给定时刻只有一个站点的断言值会变成真,所以互斥得以保证。基于仲裁团的方法:
-
分布式算法 (基于仲裁团的方法)
每个站点要得到一个子集的站点(称为一个团体)的许可后才能执行临界区。团体的形成满足如下条件:当两个站点同时请求访问临界区时,至少有一个站点同时接收到这两个请求,并且负责确保在任意时刻只有一个请求被允许执行临界区。
-
0 预备知识
系统模型
系统包括 个站点: 。假设每个站点上只运行一个单一进程。用 表示 的进程(所以在这种特殊情况下,下文中的站点 与进程 等价,后文中不做额外规定)。这些进程通过底层通信网络进行异步 (Asyc) 通信。一个希望进入临界区的进程首先给所有其他或一个子集的进程发送请求 REQUEST 消息,收到适当的回复后才进入临界区。 在等待过程中,该进程不允许发送进入临界区的后续请求。
一个站点必定处于如下三种状态中的一种:请求临界区、执行临界区以及空闲(既不请求也不执行临界区)。
许多算法采用 Lamport 逻辑时钟来给临界区的请求分配一个时间戳:时间戳用于在发生请求冲突时决定请求的优先级,通常来讲,时间戳越小的请求具有更高的优先级去执行临界区。
将采用如下符号:
- 表示调用临界区所涉及的进程或站点的数目
- 表示平均消息延迟
- 表示平均临界区执行时间
分布式算法的必备条件
分布式算法必须满足如下性质:
- 安全性:安全性规定在任何情况下只有一个进程能够执行临界区(互斥)。
- 活性:每个请求站点都应该在有限的时间内得到执行临界区的机会。活性规定不存在死锁和饥饿。
- 公平性:互斥中的公平性指每个进程都获得公平的机会执行临界区。如 Lamport 逻辑时钟顺序等。
分布式算法的性能指标
互斥算法的性能通常由以下 4 个指标来衡量:
-
消息复杂度:站点执行一次临界区需要的消息个数。
-
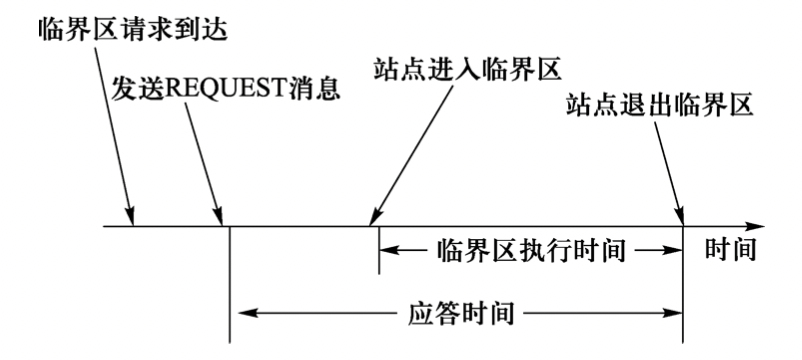
同步延迟:从一个站点离开临界区 到 下一个站点进入临界区之间所需要的事件。
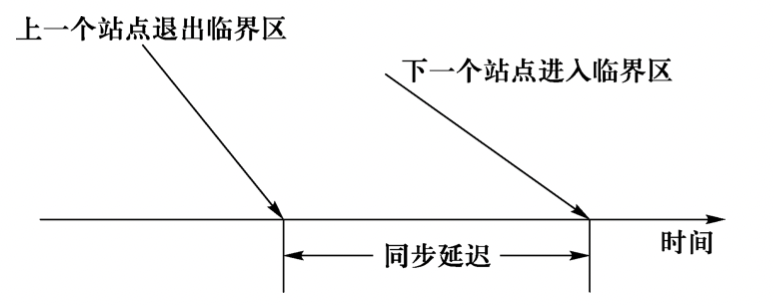
-
响应时间:应答事件。在一个请求消息发出到请求的临界区执行结束之间的时间间隔。
-
系统吞吐量:系统执行临界区请求的速度。设 是同步延迟, 是平均临界区执行时间,那么吞吐量可以由如下等式得出:
1 环形令牌算法
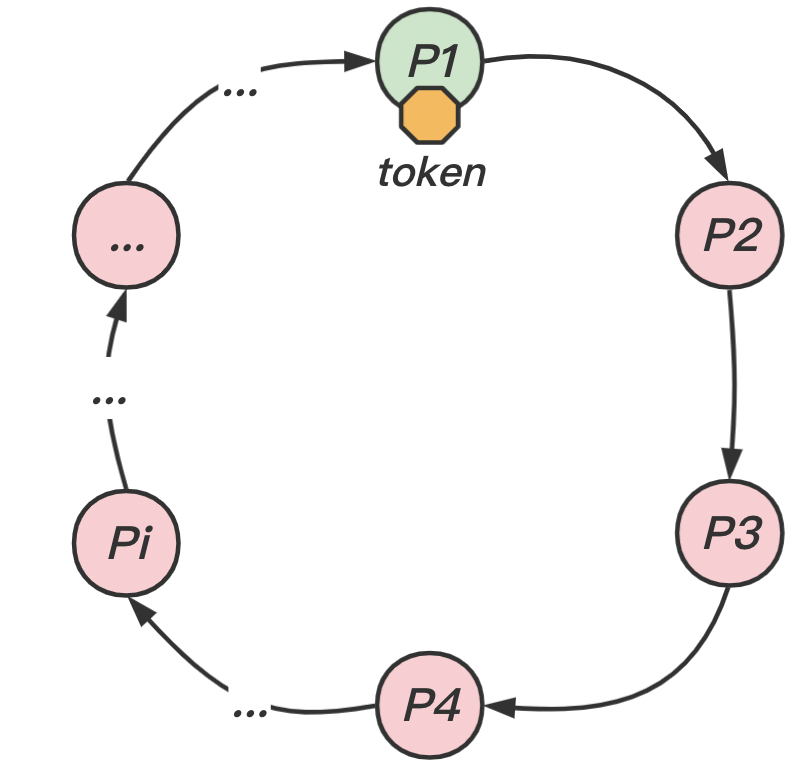
在 个进程间安排互斥而不需要其他进程辅助的方法之一,就是把进程安排在逻辑环当中。这样只要求在系统中的进程 与其下一个相邻的进程 之间存在一条通信通道。该算法的思想是通过在获得在进程间沿着逻辑环单向(例如顺时针)传递的消息作为形式的令牌来实现互斥。逻辑环的拓扑结构与站点间物理结构的互联没有关系。
算法描述
令牌按照顺时针(或逆时针)方向在程序之间传递:
- 收到令牌的进程 有权访问临界资源,访问完成后将令牌传送到下一个进程 ;
- 若该进程 不需要访问临界资源,则直接把令牌传送给下一个进程 。
伪代码描述
1 | Process P(i : 0..N-1) { |
算法分析
Lamport 算法实现了互斥,是公平的,避免了死锁和饥饿的情况。但是,不管环中的程序是否想要访问资源,都需要接收并传递令牌,所以也会带来一些无效通信。在令牌环中,若某一个程序出现故障,则直接将令牌传递给故障程序的下一个程序,从而很好地解决单点故障问题,提高系统的健壮性,带来更好的可用性。
因为在使用临界资源前,不需要像分布式算法那样挨个征求其他程序的意见了,所以相对而言,在令牌环算法里单个程序具有更高的通信效率。同时,在一个周期内,每个程序都能访问到临界资源,因此令牌环算法的公平性很好。
该算法存在的问题:
- 如果令牌丢失,需要重新产生一个令牌,但检测令牌是否丢失是比较困难的。
- 另外一个问题是进程的崩溃,但进程的崩溃比较容易检测。
- 这个算法在高负载的情况下工作很好。然而,它在轻负载的情况下工作得很差,出现很多不必要的报文传递。
2 Lamport 算法
Lamport 发明了一种分布式互斥算法用以展示时钟同步机制。该算法是公平的,且通信通道为 FIFO。具体表现为:
- 当一个站点想要请求临界区时,该站点向其他所有站点广播带有时间戳的
REQUEST请求,当收到所有其他站点返回的REPLY回复时,该站点才可以访问临界区。 - 当这个站点想要释放临界区时,该站点向其他站点广播
RELEASE释放消息。
一个临界区请求按照它们的时间戳顺序执行,并且时间是由逻辑时钟决定的。当一个站点处理一个临界区请求时,它首先更新它的局部时钟并给请求分配一个时间戳。该算法以时间戳增序执行临界区请求。每个站点 维护一个队列 request_queue,该队列包含按照时间戳排序的互斥请求。
数据结构
-
每个站点都维护一个数组 ,其初始化如下:
对于 从 接收到的所有消息,都会放入 维护数组中的相应位置 。
-
这个算法用到了三种类型的消息(均带有时间戳 与站点编号 ):
- :由站点 发出的请求临界区的消息;
- :由站点 发出,用来回应 请求临界区的消息。显然,REPLY 的时间戳要晚于 REQUEST 的时间戳。
- :由站点 发出的释放临界区的消息;
算法描述
请求临界区
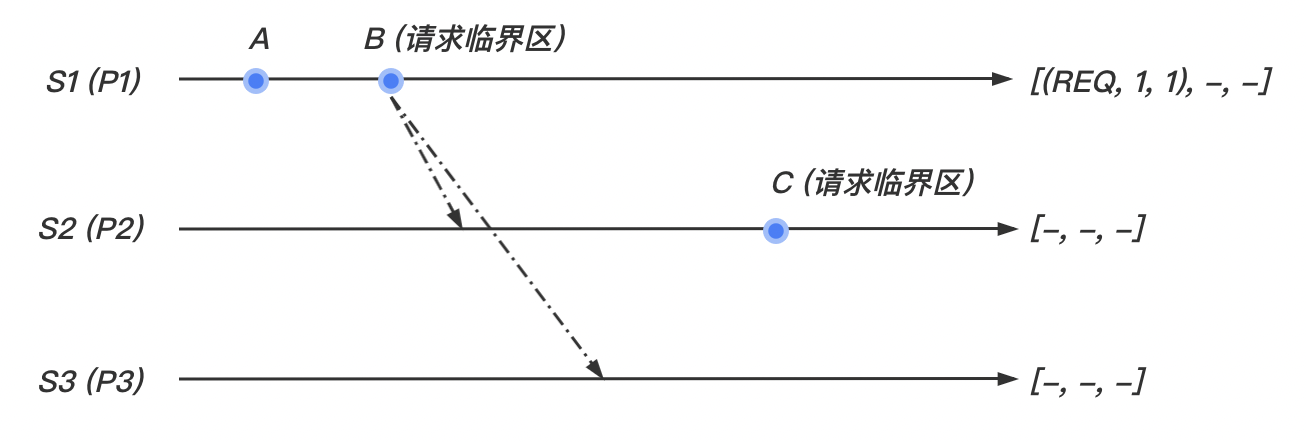
- 当站点 想进入临界区时,它广播 消息到其他站点,并且将要该消息放入自己的数组中的 位置。
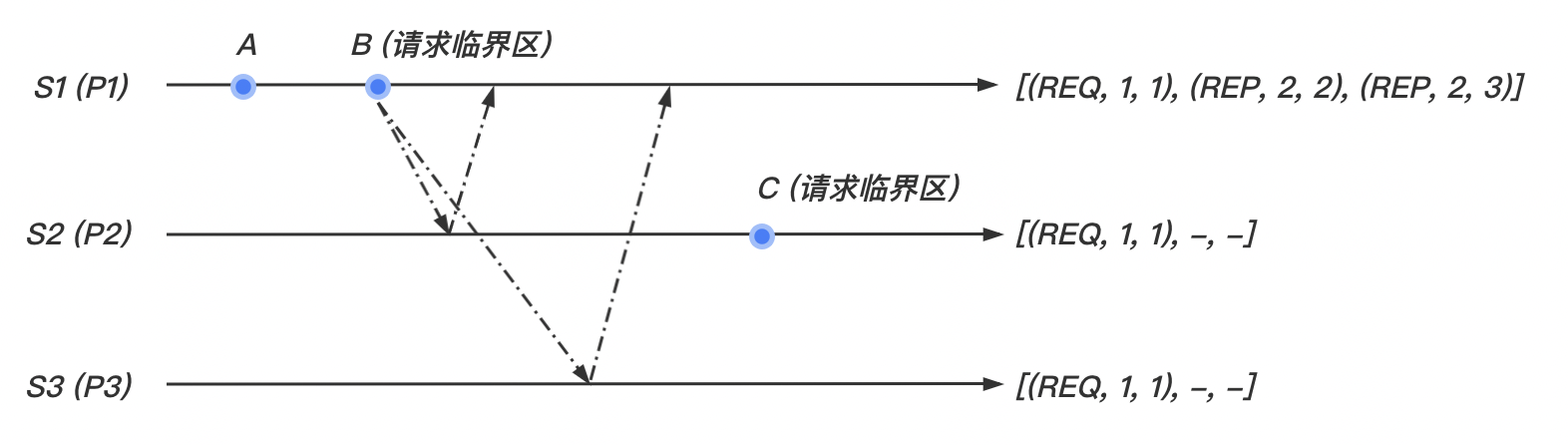
- 当站点 从站点 收到 消息, 将其放入自己数组中的 位置。如果 ,则向站点 发送更新时间戳后的 消息。
执行临界区
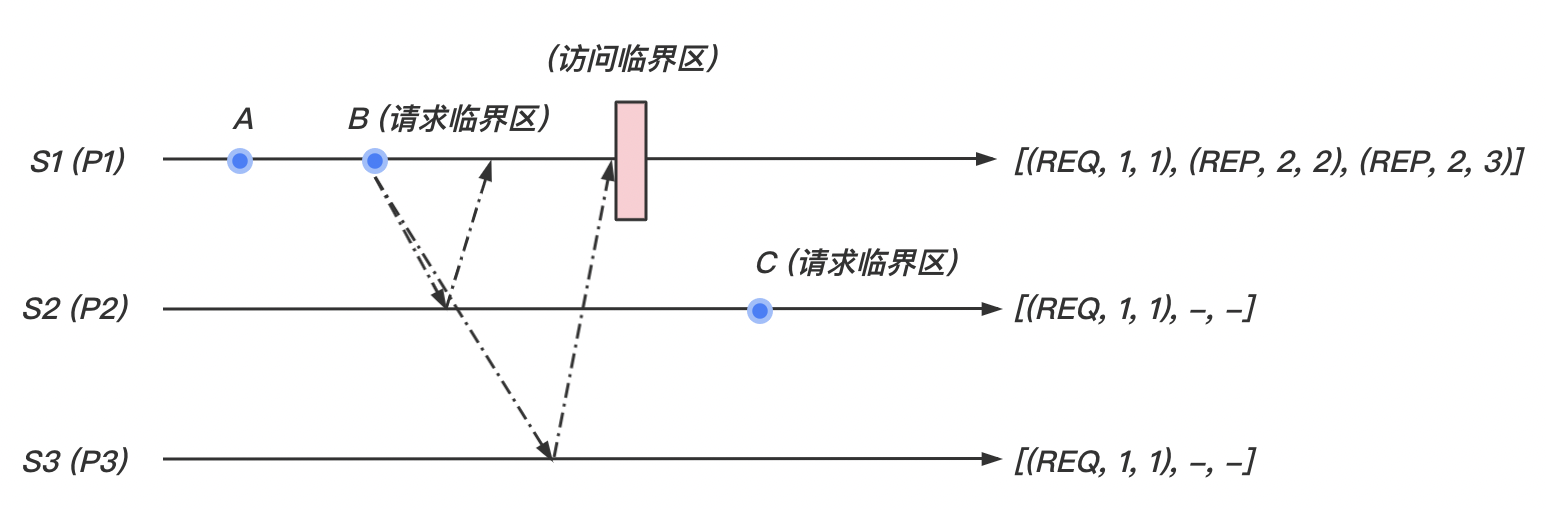
当满足以下两个条件时,站点 进入临界区:
- 站点 的数组中可以看出,当从其他任意站点接收到的消息时间戳都晚于 ;
- 消息在数组中时最早的请求消息。
释放临界区
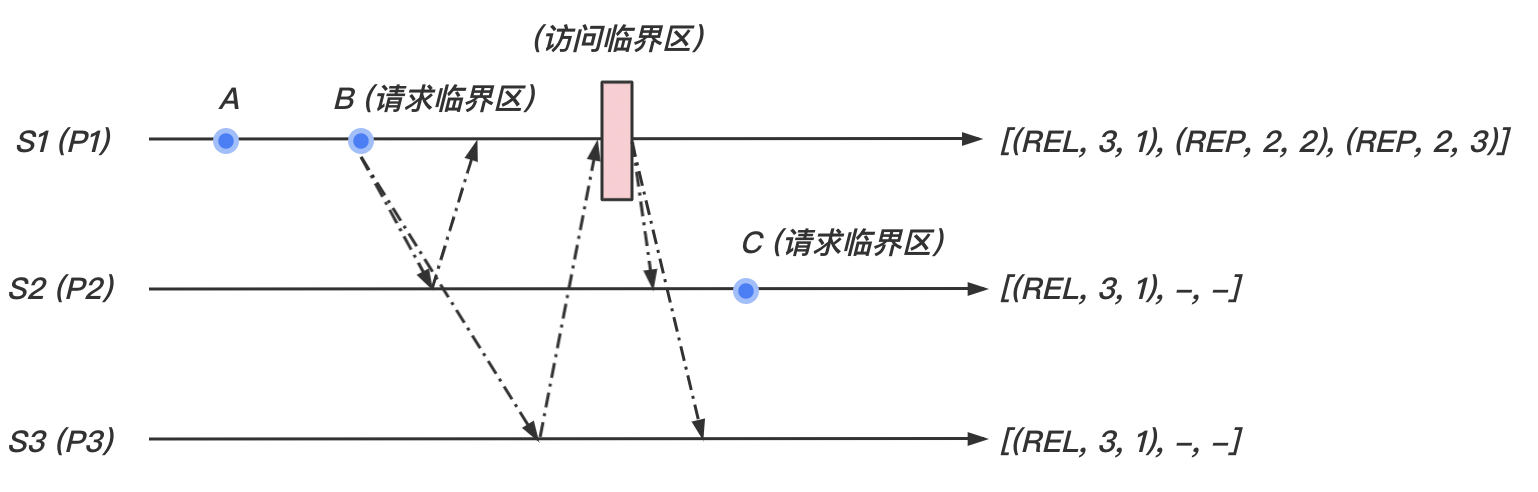
- 当站点 执行完临界区,它广播 消息到其他站点,并且将要该消息放入自己的数组中的 位置。
- 当站点 接收到 的 消息后,将该消息放入自己的数组中的 位置。
算法分析
Lamport 算法实现了互斥,是公平的,避免了死锁和饥饿的情况。
但是经过我们分析,对于每次执行临界区,Lamport 算法需要 个 消息, 个 消息和 个 消息。共 个消息,开销过大。所以我们考虑另一种优化算法。
3 Ricart-Agrawala 算法
从之前的 Lamport 算法我们可以看出,实际上 RELEASE 消息可以被取代:
- 当一个站点请求访问临界区的时候,会向其他站点发送请求。
- 如果其他站点没有访问临界区,则可以立即回复
REPLY;如果其他站点正在访问临界区或是其它原因不希望该站点访问临界区,就可以推迟回复REPLY,知道其允许访问临界区。 - 当一个站点收到其他所有站点的
REPLY消息时,可以开始访问临界区。
数据结构
在该算法中,每个站点 都维护一个推迟请求的数组 :
-
初始时,每个站点 的数组 均为 0。即,
-
一旦 推迟 的请求,则设置 的数组 。在其发送
REPLY消息后置为 。
算法描述
请求临界区
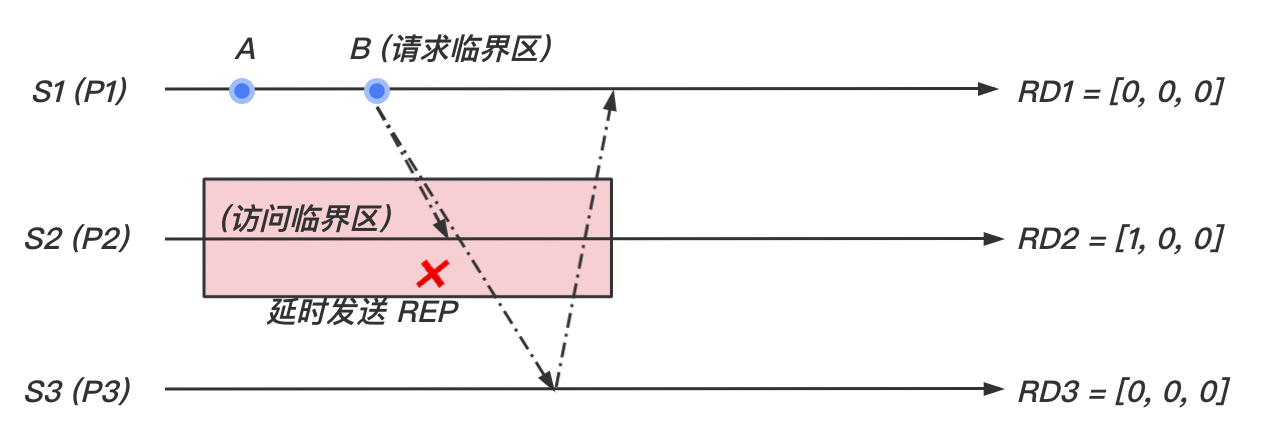
-
当站点 想进入临界区时,它广播一个带有时间戳的 消息到其他站点。
-
当站点 从站点 收到 消息,如果
- 即没有正在请求临界区也没有正在执行临界区,
- 或站点 站点正在请求临界区,但是其时间戳大于 的时间戳,
那么, 发送
REPLY消息给站点 。否则延迟发送REPLY消息,并且设置 。
执行临界区
- 从其他发送过 消息的所有站点接收到
REPLY消息后,站点 进入临界区。
释放临界区
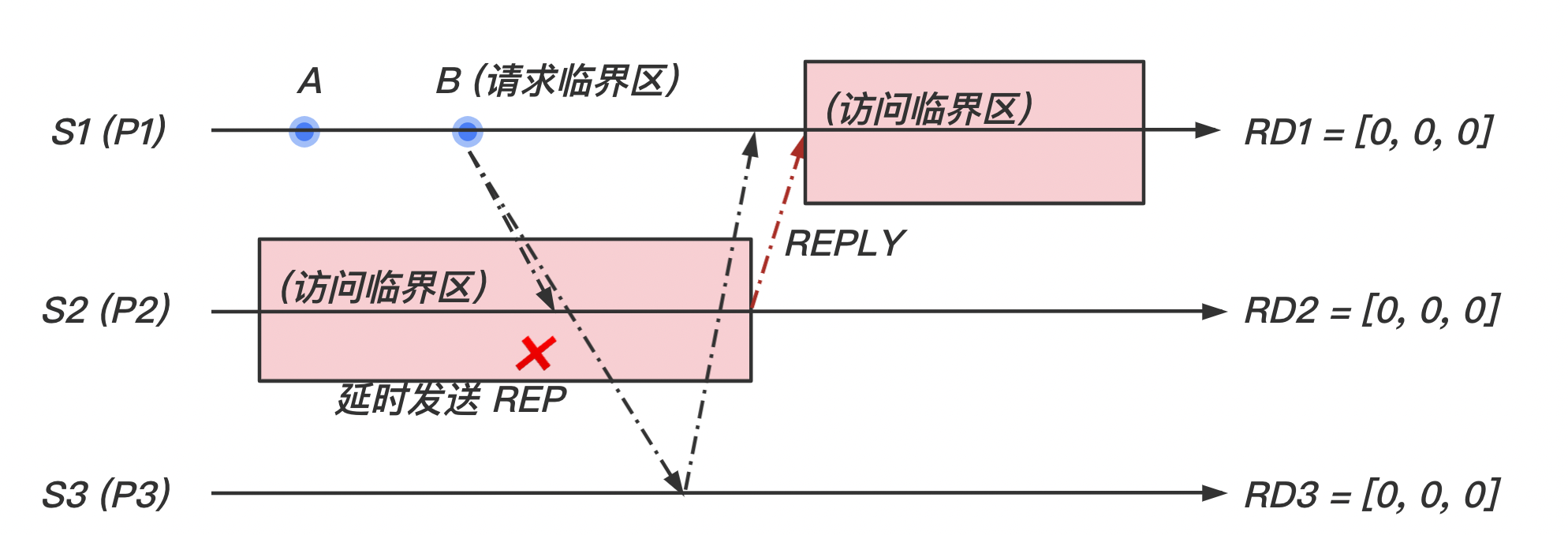
-
当站点 退出临界区时, 将发出所有延迟的
REPLY消息:对于任意 ,如果 ,则发送
REPLY消息给 ,并且设置
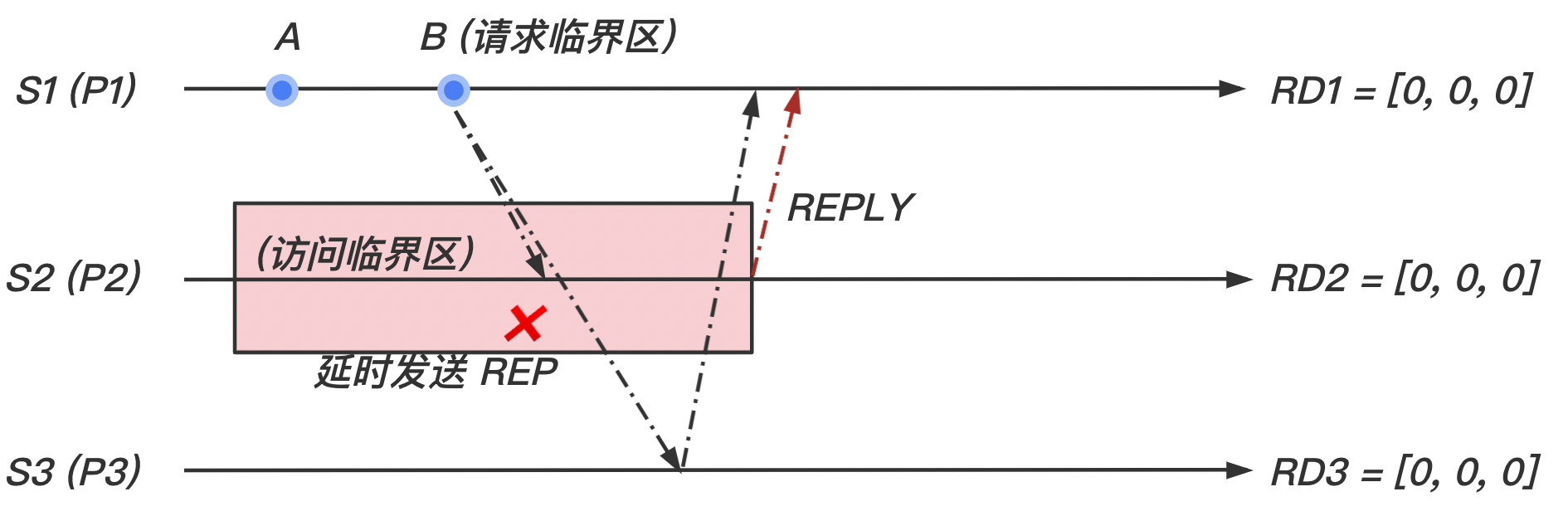
收到其他所有站点的 REPLY,开始访问临界区:
伪代码描述
1 | Process P(i : 0..N-1) { |
算法分析
Ricart-Agrawala 算法实现了互斥,是公平的,避免了死锁和饥饿的情况。
经过分析,对于每次执行临界区,Ricart-Agrawala 算法需要 个 消息和 个 消息。共 个消息,开销比 Lamport 算法更小。
4 基于仲裁团的互斥算法
基于仲裁团的互斥算法从如下两个方面开启了互斥算法的新趋势:
- 一个站点不用向所有其他站点请求许可,而只需向一个子集的站点请求许可。不同于需要系统中其他所有站点参与权限裁决的 Lamport 和 Ricart-Agrawala 算法。在基于仲裁团的互斥算法中,站点的请求集按照如下方式选择:。于是,每队站点都有一个站点来仲裁他们之间的冲突。
- 在基于仲裁团的互斥算法中,一个站点在任何时刻只能发送一个
REPLY消息。一个站点在收到前一个REPLY消息对应的RELEASE消息后才可以发送下一个REPLY消息。因此,站点 会在执行临界区之前将 中的所有站点阻塞在互斥的模式中。
基于仲裁团的互斥算法能够显著地减少在调用互斥过程中的消息复杂度,这主要是通过只询问一个子集中站点的许可实现的。
设计思想
因为这些算法是基于“圈子”(Coteries)和“仲裁团”(Quorums)的概念设计的,我们首先描述圈子和仲裁团的思想:
在一个圈子中,仲裁团满足如下性质:
- 相交性(Intersection):在一个圈子 中,对于任意的两个仲裁团 都有 。例如,集合 、 和 在一个圈子中不能作为仲裁团,因为第一个集合 与第三个集合 没有共同的元素。(保证正确性,即互斥)
- 最小性(Minimality):在圈子 中,不存在仲裁 满足 。例如,集合 和 不能作为仲裁团。因为第二个集合 真包含于第一个集合 。(保证性能,而不保证正确性)
在分布式环境中,圈子和仲裁团可以用于开发互斥算法。 一个简单的协议如下:
是仲裁团 中的一个站点。如果 想互斥访问临界区,它将请求仲裁团 中所有站点的许可。每个站点都以相同的方式调用互斥。根据相交性,仲裁团 与其他站点的仲裁团均至少有一个共同的站点。这些共同站点每次只给一个站点发送许可。因此,互斥得以保证。
在最理想的情况下:
- 每个仲裁团都有相同大小的站点数:
- 每个站点 都包含在相同数量的仲裁团中:
- 最小性:利用投影平面理论可以构造大小为 的仲裁团(理论值,详见 Maekawa 算法)。
三、终止与死锁检测
1 终止检测
通常情况下,分布式系统中一个问题的处理涉及若干进程的协作。在这种环境中,我们需要判断一个分布式计算进程是否结束,使得该进程计算结果可被使用。另外,在某些场合,有些问题会被分解成若干子问题,并且这些子问题的处理具有顺序性,某些子问题需要等待其他子问题结束方可执行。因此需要检测子问题是否终结,从而启动后续的子问题进程。
因此,分布式系统中的一个基本问题便是确定分布式计算过程何时终止。
- 分布式计算的全局终止指的是系统中所有的进程都已经终止,同时进程之间没有消息的传递。
- 本地终止是指进程的计算任务已经结束,只有接收到特定的外部消息 它才会重新启动.
1.0 分布式计算的系统模型
分布式计算是由一组固定进程构成的,消息传递是其唯一的通信方式。所有信息均会在任意但有限的延迟后被正确接收。通信是异步的,即进程发送消息的动作不依赖于接收方是否准备就绪。消息在同一个通信信道发送可能不服从 FIFO 的顺序。
分布式计算具有以下特征:
- 在分布式计算中任意一个时刻,一个进程处于下面两种状态之一:
- “活跃”状态(Active):表示进程正在做局部计算
- “空闲”状态(Passive):局部计算过程已经(暂时)结束,只能在收到另一个进程的消息 后被重新激活。
- :活跃(Active)的进程可以在任意时刻转换为空闲(Passive)进程。即当前进程已经完成局部计算,并已处理了所有收到的消息。
- :空闲(Passive)进程只有在收到来自另一个进程的消息时才能成为活跃(Active)进程。
- 只有活跃(Active)的进程才可以发送消息
- 处于活跃(Active)和空闲(Passive)的进程都可以接收消息
- 消息的发送和接收被视为原子操作
终止检测的定义:
令 表示 时刻进程 的状(活跃 Active 或空闲 Passive),表示 时刻系统中从进程 到进程 的消息数目。 一个分布式计算被认为在 时刻终止,当且仅当:
基于以上知识,我们给出一个基于环的终止检测算法:
《Detecting Termination of Distributed Computation Using Markers》Jayadev Misra
1.1 基于环的终止检测
与环形令牌算法的结构类似,我们把 个进程安排在逻辑环当中。这样只要求在系统中的进程 与其下(上)一个相邻的进程 之间存在一条 FIFO 的通信通道。我们可以在有向连通图或任意连通图上使用逻辑环来实现此算法。
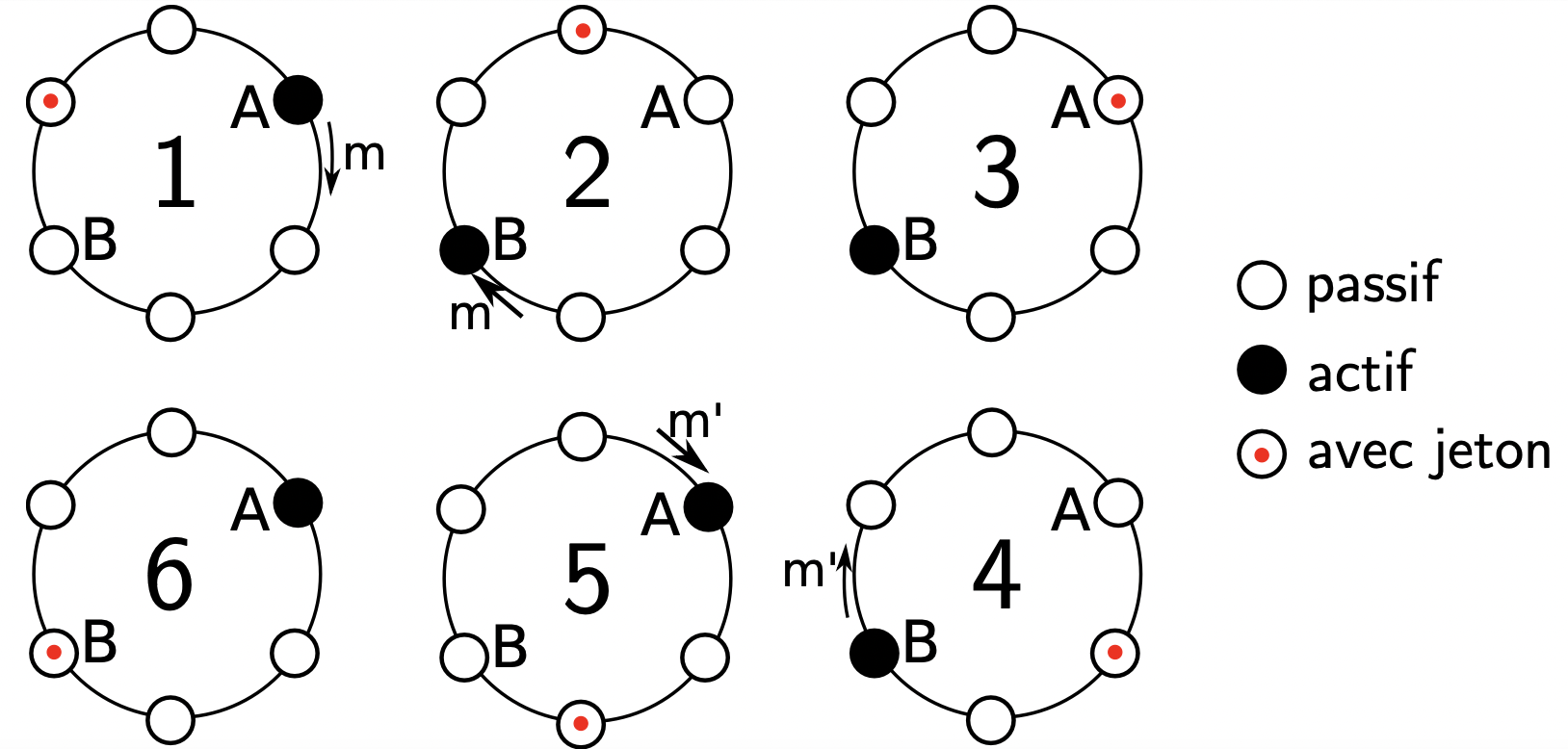
我们规定:
- 标记(
Marker或token)仅由空闲(Passive)发送;任何线程都可以接收 - 使用颜色来标记进程:
- 在任意时间点,当一个进程接收到消息时,进程使用黑色(
black)来标记; - 当且仅当一个进程发送
token,且当时进程的状态为空闲(Passive)时,进程使用白色(white)标记。
- 在任意时间点,当一个进程接收到消息时,进程使用黑色(
- 引入一个
token发送次数的计数器count:- 当
token每发送一次,计数器count=+1 - 当
token传递到一个当时状态为空闲(Passive),但是进程的颜色为黑色(即在上一轮传递中活跃 Active 过的进程)时,计数器count = 1重置为 1。
- 当
- 检测到终止:当接收到
token的线程发现计数器count等于线程总数 ,且其线程的颜色为白色时,算法检测到了终止。
伪代码描述
1 | Process P(i : 0..N-1) { |
1.2 四计数器方法
简单的计数器方法
为了检测系统中的信道是否存在消息传递,一个显而易见的方法便是让每个进程统计发送和接收基本消息的数目。 将进程 在 时刻发送的消息总数记为 ,接收的消息总数记为 。
如下图的二元组 表示各个进程在本地时间 时刻下的收发消息总数,并将其发送给启动线程。而他们组成的时间切片(time cut,图中红色虚线)又被称作“控制波动”(wave,vague)。
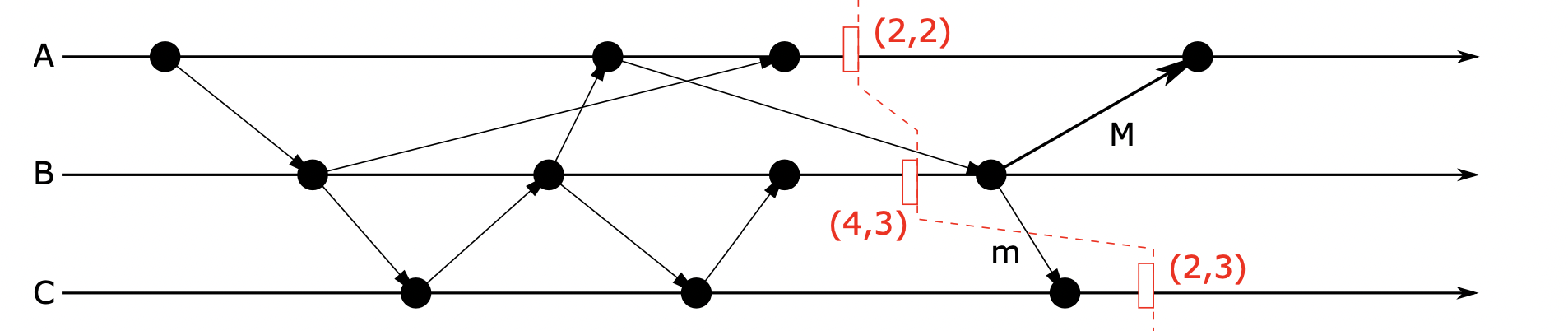
启动线程(Observateur):给定一个进程 作为检测算法的启动进程。 通过向所有进程发送控制消息(直接或者间接 )启动检测过程。假定 按照接收到控制消息的顺序排列。
我们可以在分布式系统中任意一个时刻 ,获取各个线程在本地时间 时刻发送和接收消息的总数目 。
如果初始进程的统计结果是所有进程接收消息的总和等于发送消息的总和,那么所有发送的消息都被接收,即系统中没有正在传递的消息。即
但是在如上图所示的流程图中,我们可以看到:虽然 ,但是计算并没有停止。这时我们引入四计数器方法。
四计数器方法
一个简单的解决方法是,调用两次上述的简单计数方法,两次计数方法间相隔一段时间,然后比较两次的结果。
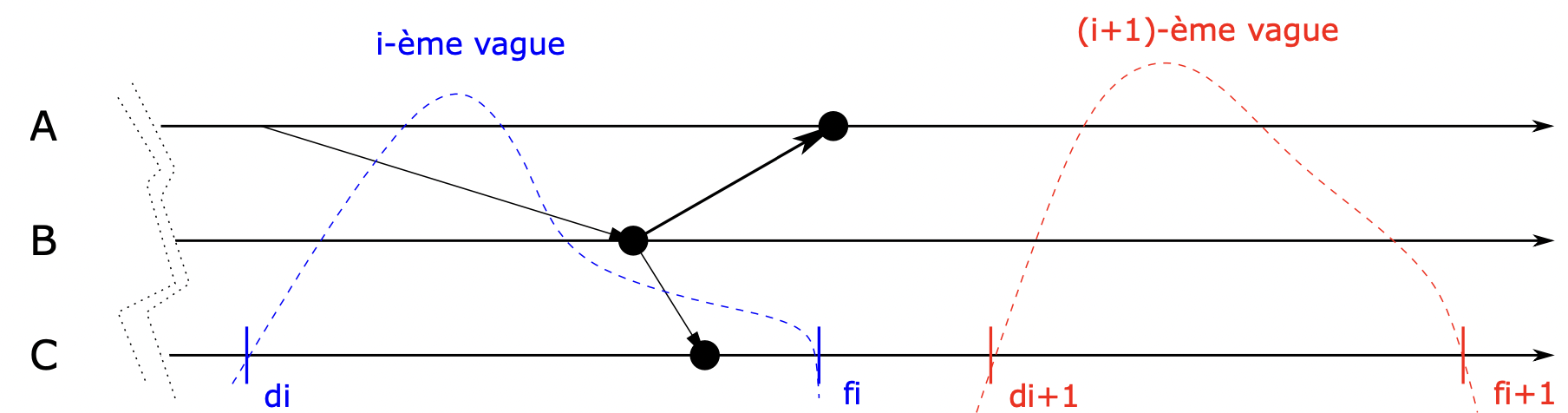
- 当第一次控制波动结束,启动线程汇总出两个计数器 和 的值。
- 启动线程发出第二次波动,同样得到两个计数器 和 的值。
- 因为本地的时间是递增的,即 ;且本地消息的计数器也是递增的,即 。所以,当 时,说明在 到 这段时间内,计算结束。
2 死锁检测
死锁是分布式系统研究中的基本问题。在理想的分布式系统中,进程可以任何次序申请资源,资源的优先级可能未知。进程可以在已占有资源的情况下,申请新的资源。如果资源分配顺序没有得到合理的控制,就会发生死锁。在系统中,组内进程申请的资源被该组中其他进程占有的状态,我们称之为死锁。
死锁有三种处理策略:死锁预防、死锁避免和死锁检测。
-
死锁预防有两种方法:进程开始执行时申请并占有它需要的所有资源;进程预先停止其他占有其需要资源的进程。(效率低,分布式系统中难以实现)
-
死锁避免的方法:如果将资源分配给请求进程后,整个系统处于安全状态,那么就将该资源分配给请求进程。(需要知道系统的全局状态,效率低,分布式系统中难以实现)
-
死锁检测需要检查当前进程 - 资源的占有关系,找到死锁条件(1 检测现存的死锁)。并通过终止产生死锁的进程来解决死锁问题(2 已检测出死锁的解锁)。
死锁检测算法必须满足以下两个条件:
- 可执行性(活性);算法必须检测出有限时间内所有存在的死锁。发生死锁后,死锁检测算法能照常运行,直到死锁检测出来为止。换句话说,当死锁形成之时,算法无需等待其他事件发生即可检测死锁。
- 安全性:算法不能报告本不存在的死锁,即错报死锁。在分布式系统中,由于缺乏一个全局时钟,过期的不一致信息可能会导致站点检测到一个不存在的环,这个环的不同边存在于系统中的不同时刻。从而造成误判。
系统模型
我们将整个系统可用一个有向图来表示:图中节点代表进程,边代表通信信道。并且做了如下假设:
- 系统只拥有可重复使用的资源
- 进程采用独享的方式访问资源(互斥访问)
- 每种资源只有一个拷贝(无本地备份)
进程可以有两种状态,运行状态和阻塞状态:
- 在运行状态下,进程拥有它需要的资源。此时进程要么正在执行,要么正准备执行;
- 在阻塞状态下,进程等待获取运行所需要的资源。
等待图
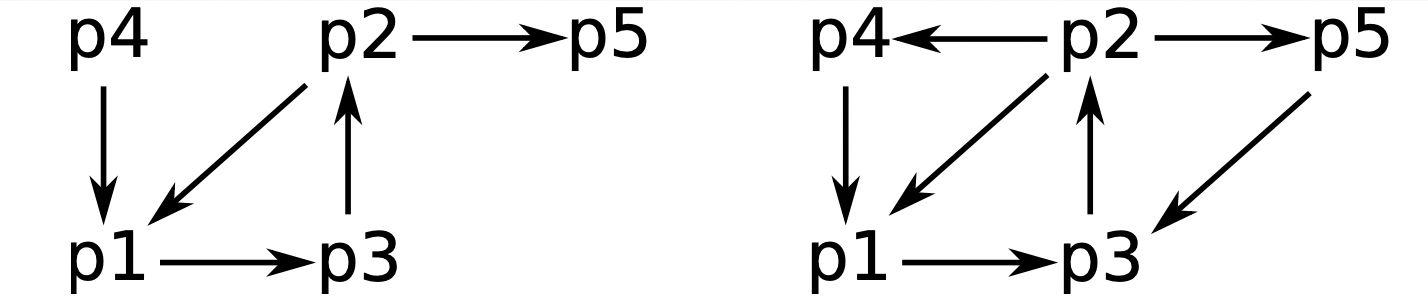
分布式系统状态可以用有向图来描述,如图所示,这个有向图也叫等待图(***W***ait-***F***or ***G***raph)。在 WFG 中,
- 节点:节点代表进程。
- 有向边:如果 处于阻塞状态并且正在等待 释放资源,那么图中存在一条从 节点指向 节点的有向边。
当且仅当等待图 WFG 中存在有向环或结时,系统中存在死锁。
结(knot)的本质依然是一个环:如果节点 可以到达的任意节点 都可以在此返回节点 ,那么节点 在结中。即节点 是多个环中的公共节点。
单资源模型
该模型中进程最多只有一个单位的未完成资源请求。因此,该模型下 WFG 图中节点的最大出度为 1,图中的环即代表死锁。
AND 模型
在 AND 模型中,进程同时请求多个资源。只有当所有请求的资源都能得到满足时,系统才将资源分配给该进程。被请求的资源可以在系统的任何位置。在 AND 模型下,WFG 图中节点的最大出度可以大于 1。 图中的环代表死锁。

在如图所示的 WFG 图中,左侧的图中 只有在两个资源都满足时才会被激活。因为存在 的环,所以该系统存在死锁。
OR 模型
在 OR 模型中,一个进程同时请求多个资源。其中任意一种资源能满足则立即将该资源分配给进程。被请求的资源可以在系统的任何位置。在 OR 模型下,WFG 图中的环不一定代表死锁。在某一个进程出发,资源请求的所有边上,都有一个包含该进程节点的环(即为结),则说明存在死锁。

在如图所示的 WFG 图中,右侧的图中 只有在两个资源中满足任意一个时就会被激活。但是因为存在 环 、环 以及环 所组成的结,所以该系统存在死锁。
死锁检测算法
分布式死锁检测算法可以分为 4 类:路径推送算法、边探测算法、基于计算分散的算法、基于全局状态检测的算法。
由于课程需要,这里只介绍基于计算分散的算法。其余算法恕不作讨论。
基于计算分散的算法
- 进程向 WFG 图中该进程所有出边发送请求消息,这些消息通过 WFG 图中的边得以传播(即分散)
- 正常执行的进程直接丢弃该消息,阻塞的进程收到该消息后有以下处理方式:
- 当阻塞进程第一次收到触发死锁的站点发来的请求消息时,它不会立即向请求的进程立即回复该请求。而是继续向它的所有出边发送请求消息,只有当它收到发出的所有请求消息的回复后(向 WFG 图中它的后继节点),才向请求的进程发送回复。
- (非第一次)对于所有死锁检测触发进程后的请求,收到请求的进程立即回复该请求。
- 当死锁检测触发进程收到它发出的所有请求的回复,说明系统存在死锁。
该类型的死锁检测算法包括 Chandy, Misra, Hass 针对 OR 模型的算法。
我们使用一个例子来解释:在如图所示的 WFG 图中, 进程节点是作为触发死锁检测的进程。
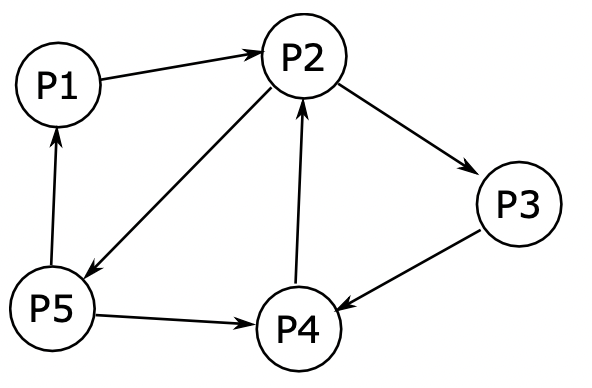
我们可以根据上述的算法,画出如下的分析图。
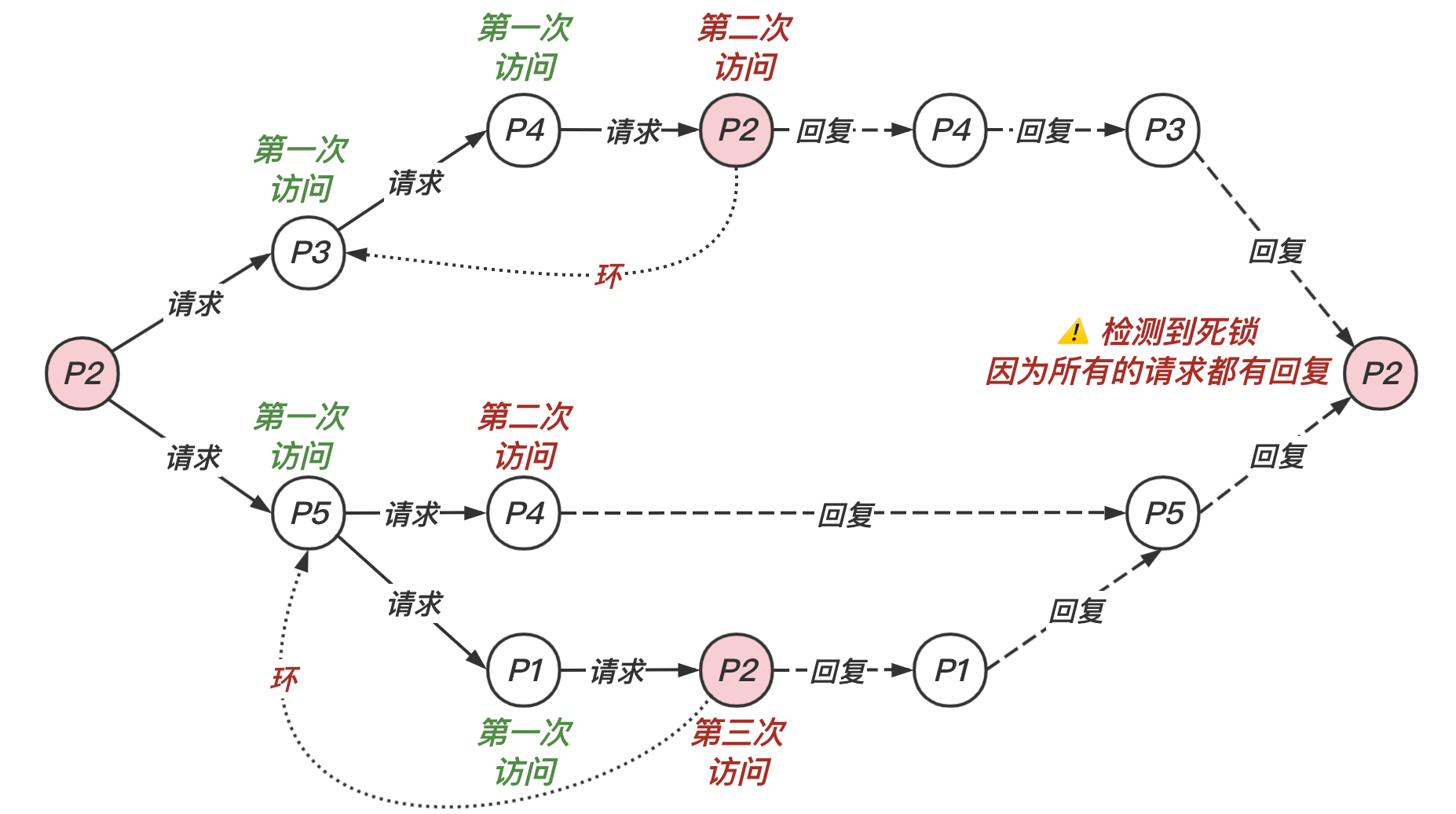
四、共识与故障检测
1 共识问题
在分布式系统中,进程之间达成一致对于很多应用程序是一个基本的需要。很多形式的协调需要进程之间相互交换信息、彼此协商,最终在进行下一步行动前达成共识。共识是容错(tolerance)的通用工具。一些问题依然可以通过共识来解决:
- 选举问题:在多个进程中选举出一个每个进程都同意的领导进程(leader)
- 分布式事务的提交操作:!各个进程共同决定是否提交 或者终止它们共同参与的事务
- …
本节将介绍共识问题、相关的拜占庭将军问题和交互一致性问题。粗略地说,这些问题是在一个或多个进程中提议了一个值应当是什么后,使进程对这个值达成一致的意见。我们在此仅就共识问题展开讨论。
系统模型
我们的系统模型包括一组通过消息传递进行通信的进程 。 在许多实际情况下,一个重要的要求是,即使有故障也应能达成共识。在我们的系统模型中,我们做出如下的假设:
- 【故障模型】:在系统 个进程中,最多有 个可能出错。出错的进程可以是崩溃故障(Crash failure)发送遗漏(Omission failure)、接收遗漏(Omission failure)拜占庭故障(Byzantine failure)等。其中:
- 崩溃故障(Crash failure):一个进程可能在某一步操作中崩溃。它可以是本地操作,也可以是发送或接收消息的遗漏(Omission failure);
- 拜占庭故障(Byzantine failure):一个进程可进行任意行为。
- 【同步/异步通信】:一个易于出错的进程向 进程发送消息失败时,
- 在异步系统中: 无法探测到这条没有到达的消息。因为这一情况不能与消息传输花费很长时间的情况区分开来。我们将在考虑任一故障模型下的异步系统中达成一致的不可能性时再讨论这一问题
- 在同步系统中:一条消息没有发送成功可以在回合结束时被预期的接收者识别出来。
- 【网络连接】:系统是全连接的。每一个进程可以与其他进程直接进行通信(通过消息)
- 【发送方身份识别】:接收消息的进程总是可以知道发送进程的身份。
- 【通道可靠性】:传输通道是可靠的,并且只有进程可以出错(在各种故障模型中)。
- 【认证消息与未经认证的消息】:
- 对于一个未经认证的消息:当出错进程转发消息给其他进程时,它可以伪造消息,并声称该消息是从另一个进程接收到的;它也可以篡改收到消息的内容再转发给其他进程。当一个进程接收到一条消息时!它没有办法验证消息的真实度。
- 通过诸如数字签名之类的技术可以实现消息的认证。如果某个进程伪造了消息或是消息转发前篡改了内容后,接收者能够探测出来。
- 【决定(协定)变量】:协定变量可以是二元类型(0/1)、布尔类型的,也可以是多值的,而且不一定是整数。
共识问题的定义
为了达到共识,每个进程 最初处于未决(undecided)状态,并且提议集合 中的一个值 。进程之间互相通信,交换值。然后每个进程设置一个决定变量(decision variable) 的值。在这种情况下,进程进入决定(decided)状态。在此状态下,进程将不再改变 。
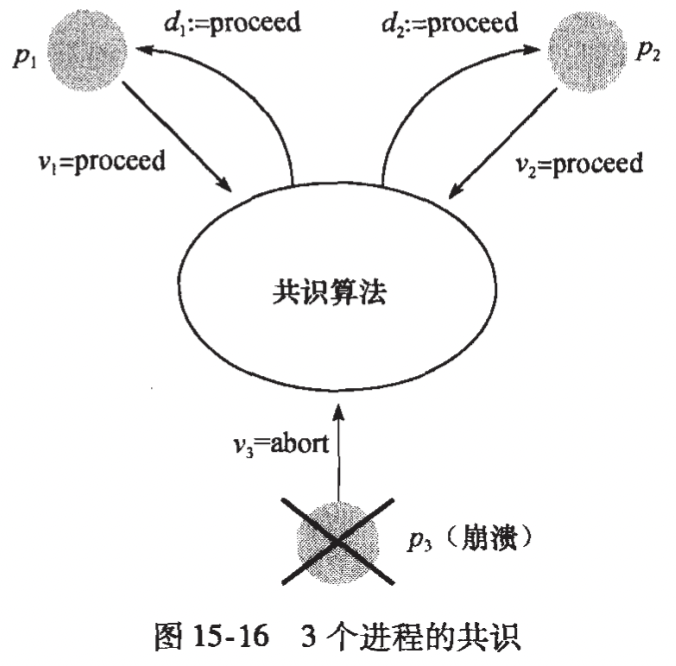
上图是一个共识问题的例子:两个进程 提议“继续”(processed),第三个进程 提议“放弃”(abort)但是随后崩溃(即出错)。保持正确(非出错)的两个线程都决定“继续”。
共识算法要求在每次执中都满足以下条件:
- 协定性(Accord):所有正确的进程的决定值 都相同。即,如果 和 都是正确的,且已经进入决定状态,那么 。
- 完整性(Intégrité):如果所有正确的进程都提议同一个值,那么处于决定状态的任何正确进程都决定了这个值。且任何进程最多只能做出一次决定。
- 有效性(Validité):是一种较弱的完整性。决定值是某些正确进程的提议的值之一。
- 终止性(Termination):每个正确(非出错)进程最终会都将决定(设置一个确定的决定变量 )。
拜占庭将军问题
该问题源于中世纪拜占庭帝国发动的战争。进攻方有 4 个兵营,各由一个将军指挥,围绕着拜占庭城堡驻扎。
- 他们只有同时攻城才可以成功。因此,他们需要在进攻时间上达成一致。
- 兵营之间通信的唯一方式就是派送报信人(报信人可以抽象为消息)。
- 报信人在两兵营之间可花费无限制的时间(可以抽象为一个异步的系统)。
- 报信人被敌人抓住(抽象为消息的丢失)
- 叛变的将军可以看做一个拜占庭进程,叛徒会试图破坏达成协定的机制。例如给其他将军发送误导性的信息。例如,叛徒可以给一个将军说上午 10 点进攻,而通知其他将军中午 12 点发起攻击;或者他可以不给某个将军发送任何消息;他也可以在转发前,篡改从其他将军得到的消息。
抽象的模型如下图所示:
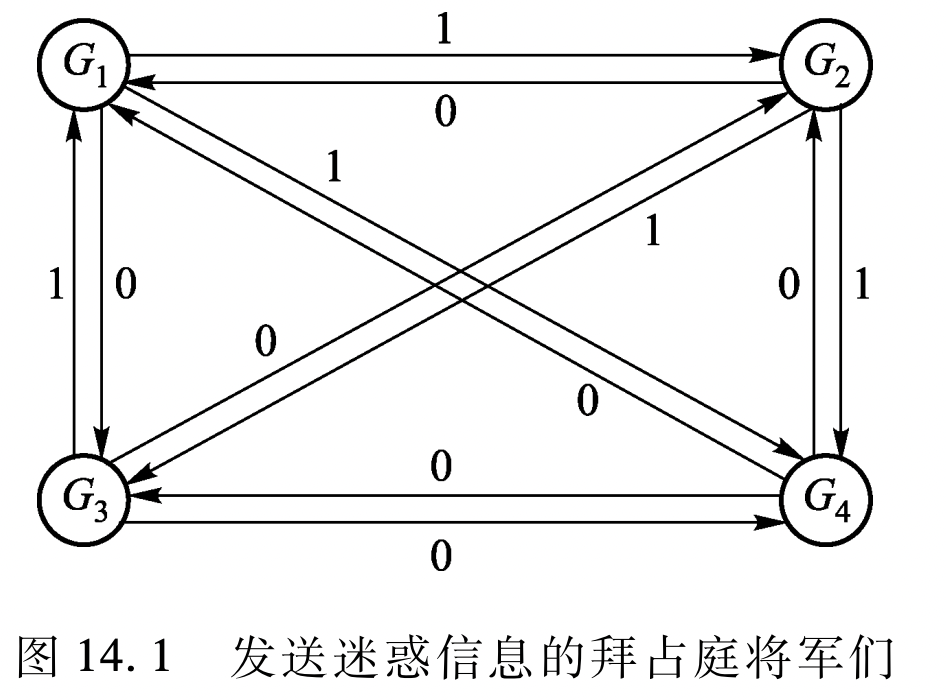
拜占庭将军问题与共识问题的区别在于:拜占庭问题中指定了一个独立的源进程来提议一个值 ,由其他进程决定是否决定采纳这个值;而后者是每个进程都会提议一个值 。
相似地,拜占庭将军问题要求在每次执中都满足以下条件:
- 协定性(Accord):所有正确的进程的决定值 都相同。即,如果 和 都是正确的,且已经进入决定状态,那么 。
- 完整性(Intégrité):如果源进程是正确的(不出错),所有正确(非出错)进程决定的值 必须与源进程的初值 相同。且任何进程最多只能做出一次决定。
- 终止性(Termination):每个正确(非出错)进程最终会都将决定(设置一个确定的决定变量 )。
结果概观
我们这里先给出解决共识问题的结果概览。列出了在不同假定条件下,解决共识问题的下界。
对于“无故障”情况,共识是可达成的。在同步系统中,对协定值的共识也是可以达到的。而在异步系统中,对协定值的并发的统一认识也是可以达到的。
在下表中, 表示倾向出错的进程数目, 表示进程的总数目。
| 故障模式 | 同步系统(消息传递和共享内存) | 异步系统(消息传递和共享内存) |
|---|---|---|
| 无故障 | 可以达成协定值的共识 | 可以达到协定值的并发的共识 |
| 崩溃(Crash) | 可以达成协定 |
不能达成协定 |
| 遗漏(Omission) | 可以达成协定 |
不能达成协定 |
| 拜占庭故障 (Byzantine) |
可以达成协定 |
不能达成协定 |
在异步系统中即使只有一个进程发生故障,共识问题都是不可解的。围绕这个 不可能的结果,下表中定义了一些弱化的共识问题的变体。表中给出的开销(复杂度)是针对所描述的算法的。
| 可解的变种 | 故障模型及开销 | 定义 |
|---|---|---|
| 可靠广播问题 | 崩溃故障 |
有效性,协定,完整性条件 |
| - 共识问题 | 崩溃故障 |
达成共识值的集合大小不超过 |
| - 共识问题(近似共识) | 崩溃故障 |
达成共识的值彼此之间相差不超过 |
| 重命名问题 | 崩溃故障 |
从名字集合里选择一个唯一的名字 |
下图进一步展示了异步的消息传输系统和共享内存系统是 如何试图解决共识问题的:
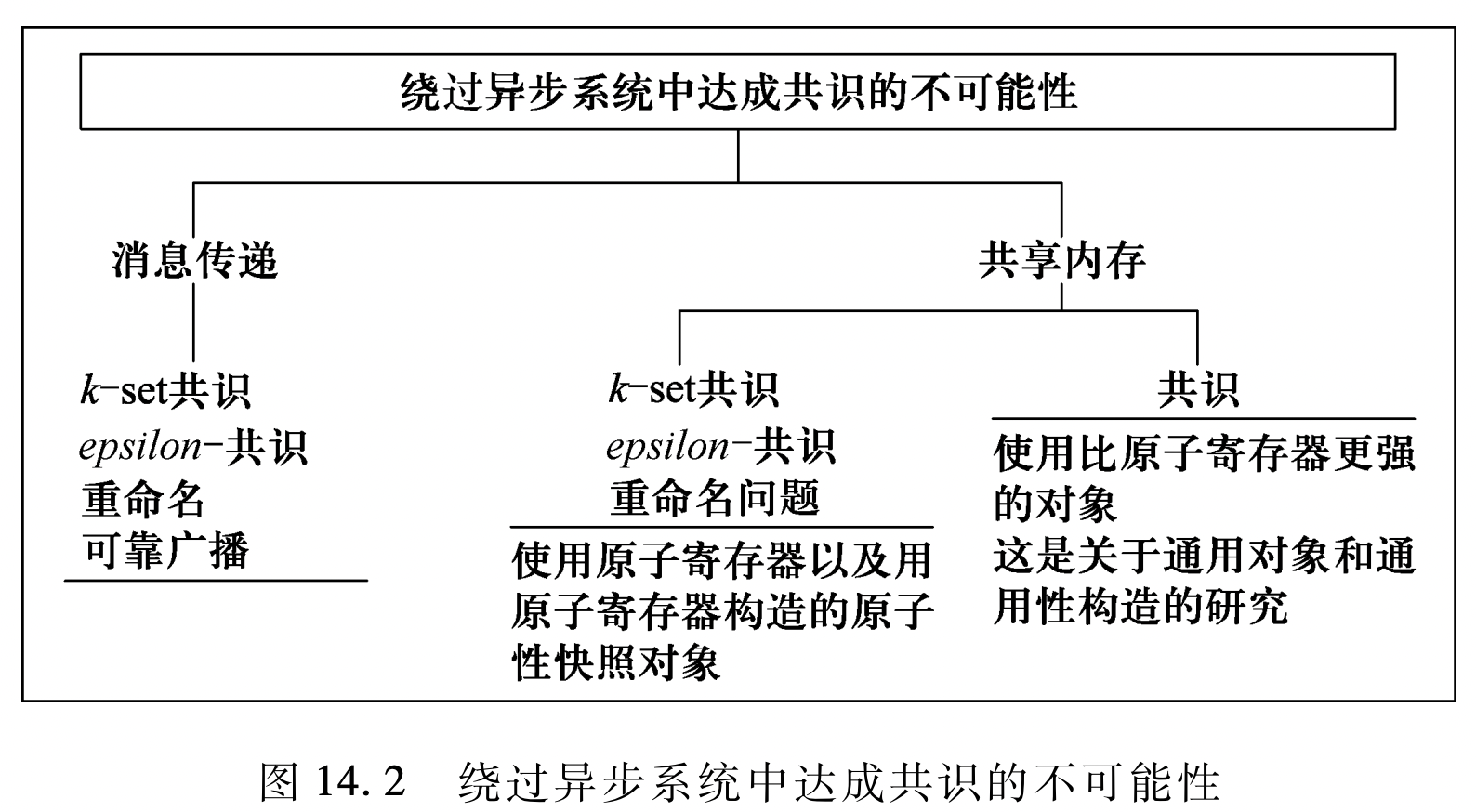
2 同步系统中的协定问题
无故障的情况
在无故障系统中,可以通过从不同的进程收集初始信息,决定一个结果,然后把它分发到整个系统中去,从而解决共识问题。分发机制可以让每一个进程向其他进程广播它的值。最终结果的生成会使用应用程序相关的函数得到如取多数、最大值及最小值等。
伪代码描述
1 | Processus Pi(vi), // 其中 1 ≤ i ≤ n |
崩溃故障的情况
在处理崩溃故障模型的 个进程中,最多有 个进程可以失败的情况(容错,Tolerance)。
这里,共识变量 是一个整数值。每个进程有一个初始值 。如果最多可以容忍 个进程失败,那么这个算法就需要执行 个循环。在每个循环中,如果这个值之前没有被发送过,进程向其他进程发送它的值 。然后每个进程从每轮循环中接收到的值以及循环开始时的 中,挑选一个最小值作为下一轮循环开始时的 。 轮循环之后,各个进程的 就可以保证是共识值。
伪代码描述
1 | Processus Pi(vi), // 其中 1 ≤ i ≤ n |
算法分析
- 一致性(Accord)条件可以满足:因为在 次循环中,至少存在一个循环,其中没有任何进程发生故障。在这一轮循环 中,所有进程成功地广播了它们的值。而且所有的进程都取广播值和接收到的值的最小值。因此这轮循环过后,所有进程得到的值都是一样的,即为 。在之后的循环中,只有这个值可以被发送,且每个进程最多只可能发送一次,不会有进程再回去更新 的值。
- 有效性(Validité)可以得到满足:因为在这一故障模型中,进程不会发送虚假的值。因此,一个进程在发生故障前,只会发送正确的值。对于所有进程 ,如果它的初始值 是相等的,那么任何进程发送的值只可能是一致性条件中的共识值。
- 终止性(Termination)条件显然可满足:算法总会在经过 轮循环后结束。
- 复杂度:该算法执行 次循环,其中 。每轮循环中,消息的数目最多为 。每条消息有一个整数。因此所有的消息数目为 。最坏的情形如下:假设最小的值最初只由一个进程所有。在第一轮循环中!该进程失败前只把它的值发送给了另外的一个进程。在接下来的循环中,拥有最小值的这个进程在失败前都只把该值发送给另外的一个进程。
- 循环次数的下界值:至少需要 次循环,其中 。所谓下界,对应于最坏情况时的情形,也就是进程在每一个循环中都可能失败,而 次循环就至少有一次循环中没有失败发生。
拜占庭崩溃的情况
个进程组成的同步系统中,拜占庭协定问题(以及协定问题的变种)是可解的,仅当拜占庭进程的数目 满足 时。
我们用下面的两个步骤,非严格地证明这个结果:
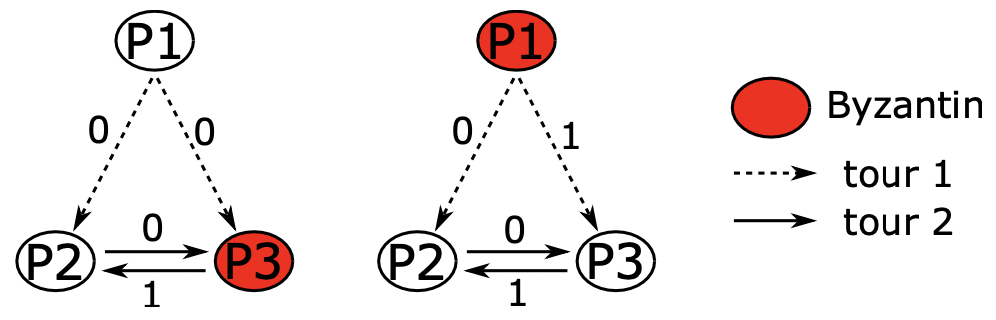
- 当 时,如果拜占庭进程数 ,拜占庭协定问题是不可解的。我们使用如上图所示的图示来说明。图中有一个指挥官 和两个副官 和 。
- 在第一种情况中(左图),恶意进程为 ,进程 忠实地接收指挥官进程 的值(0);
- 在第二种情况中(右图),恶意进程为指挥官进程 ,其向两个忠诚的进程发送了不同的命令(向 发送 0,向 发送 1)
对于进程 来讲,它无法区分这两种情况。而且接下来的任何消息交换都不再有用,因为每个进程已经把它从第三方进程获得的信息传达出去了。这两种情形下,进程 从其他两个进程得到了不同的值。导致其无法做出一个能在两种情况下都正确的决定。所以当 时, 时,不能达成共识。
- 时,拜占庭协定问题是不可解的。
Phase King 算法
该算法需要 轮循环(Phase),仅需要多项式级别()的消息,这是一个非常大的空间节省,但只能接受能够忍受至多 个恶意进程。该算法之所以取名为 Phase King,是因为它分 个阶段,每个阶段包括两个回合,每个回合中都有一个唯一的进程扮演非对称的领导角色(King)。下图显示了该算法消息发送的模式:
- 回合 1: 在每个阶段的第一个回合中,每个进程将它对共识值的估计值广播给所有其他进程,并等待来自其他进程的广播。这个回合结束时,它会计算
true (1)和false(0)的票数。如果某一个的票数超过 ,那么就把它设置为共识值,并设置mult变量为它的票数。如果没有一个超过 ,这种情况发生在恶意进程没有响应,其他进程的投票分布在true (1)和false(0)中,这时取默认值来设置majority。 - 回合 2:在每个阶段的第二个回合,本阶段的 King 开始初始化处理, 作为第 阶段的 King。
下面我们给出 Phase King 算法的伪代码:
算法伪代码
1 | boolean: vi <- 初始值; |
五、分布式共享内存
分布式共享内存(Distributed Shared Memory,DSM)是提供给分布式系统程序员的抽象概念。程序员编程使用读写原语(READ() / WRITE())通过网络访问数据,而不必处理发送和接收等通信原语,以及随之而来的信息交互模型中复杂的同步和一致性操作。
DSM 后台本质上是一个分布式网络,并且数据需要在该系统中实现在某种方式下的共享。但是不利的情况在于,该系统随时都可能发生数据复制和并发访问,我们还需要加入并发控制机制。具体来说,当多个处理器希望访问相同的数据对象,这些访问的先后顺序需要被确定。另一方面,如果允许多个处理机并发访问不同的副本,副本的一致性问题(缓存一致性问题)有待解决。
1 内存一致性模型
参考:周刊(第22期):图解一致性模型 - codedump’s blog
内存连贯性是系统内存操作正确执行的重要保证。传统正确的内存操作定义为读操作的变量返回值为最近一次写操作修改后的值。在 DSM 系统中,“最近一次”在并发访问和多副本系统中变得模棱两可。
DSM 系统规定了多种内存一致性模型,程序员写程序时需要知道他们的一致性符合哪种特定模型。我们主要研究 6 种一致性模型:
强一致性
在传统单处理器机上,读取某位置变量时应返回最近一次写入该位置变量值。在分布式系统中,最严格的这种模型我们称之为强一致性模型。
这种模型的两个突出特点为:
- 在单处理器中存在一个共同的隐式全局时钟
- 写操作对所有进程立即可见
这两种要求可以被同时满足吗?
可以。强一致性因需要全局时钟而具有很大的开销,同时所有的处理器需要遵循共同次序。实现时我们使用全序。为简便起见,我们在每个处理器保存一个全序副本,由广播机制确保操作次序在所有处理器上一致。
伪代码描述
1 | int : x; |
算法分析
在该算法中,广播机制保证了所有处理器看到相同的操作次序:
- 对于两个不同处理器上的不重叠操作,在全局时钟下,前一个请求的响应发生在后一个请求的响应之前。
- 对于两个重叠操作,全序保证了所有处理器看到相同的次序视图。
-
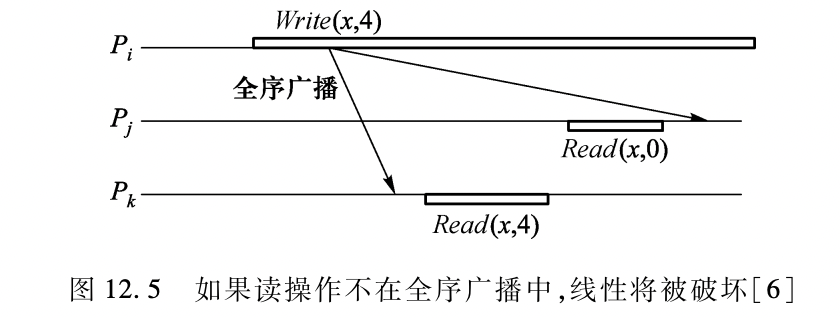
在算法中(13-15行),为什么收到收到来自网络的关于读操作的全序广播后,不做任何操作呢?
目的是为了使读操作也参与排序。如果读操作不在全序广播中,该读操作不能与其他读写操作一起排序,这便破坏了强一致性的要求。如下图。
顺序一致性
在分布式环境中,强一致性因为全局时钟限制很难实现。程序员开始寻找条件不那么苛刻的模型。
Lamport 利用逻辑时钟代替全局时钟提出顺序一致性。顺序一致性的定义最初出现在论文*《How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Progranm》*中,原文中要求顺序一致性模型满足两个要求:
- 所有执行结果相同,就像处理器的所有操作是在一定的顺序下执行的一样
- 在本地时钟下,本地操作顺序为本地程序的执行顺序
“the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.”
(任何执行的结果都与所有处理器的操作按某种顺序执行的情况相同,每个单独的处理器的操作按其程序指定的顺序出现在这个序列中。)
它有两个条件:
Requirement Rl: Each processor issues memory requests in the order specified by its program.
Requirement R2: Memory requests from all processors issued to an individual memory module are serviced from a single FIFO queue. Issuing a memory request consists of entering the request on this queue.
条件 1:每个进程的执行顺序要和该进程的程序执行顺序保持一致
条件2:对变量的读写要表现得像FIFO一样先入先出,即
每次读到的都是最近写入的数据
我们考虑如下几个例子:
【例 1 】 和 的初始值为 0
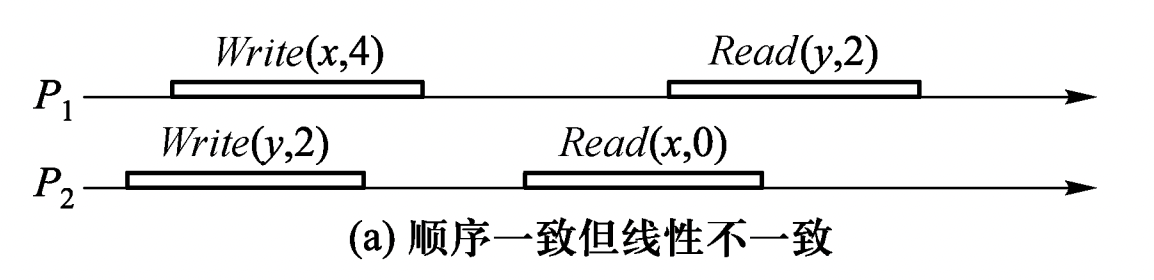
从图上看,进程 , 的顺序一致性并没有冲突。因为从这两个进程的角度来看,顺序 应该是这样的:
1 | Write(y,2) -> Read(x,0) -> Write(x,4) -> Read(y,2) |
这个顺序对于两个进程内部的读写顺序都是合理的,只是这个顺序 与全局时钟下看到的顺序并不一样。在全局时钟的观点来看, 进程对变量 的 Read() 操作在 进程对变量 Write() 的写操作之后,然而 读出来的却是旧的数据 0。
【例 2】
情况 1:
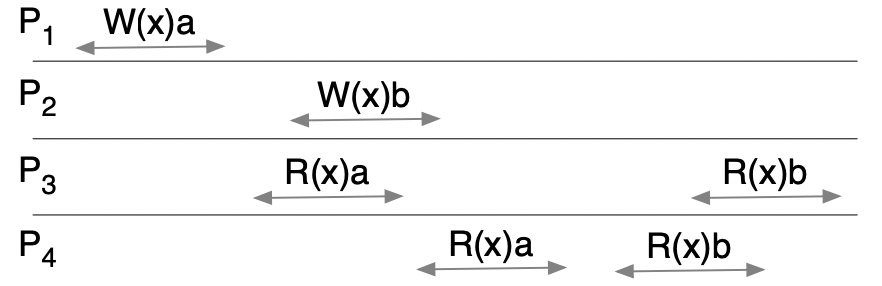
该情况满足顺序一致性的,顺序之一的 为
1 | P1:W(x)a -> P3:R(x)a -> P4:R(x)a -> P2:W(x)b -> P3:R(x)b -> P4:R(x)b |
情况 2:
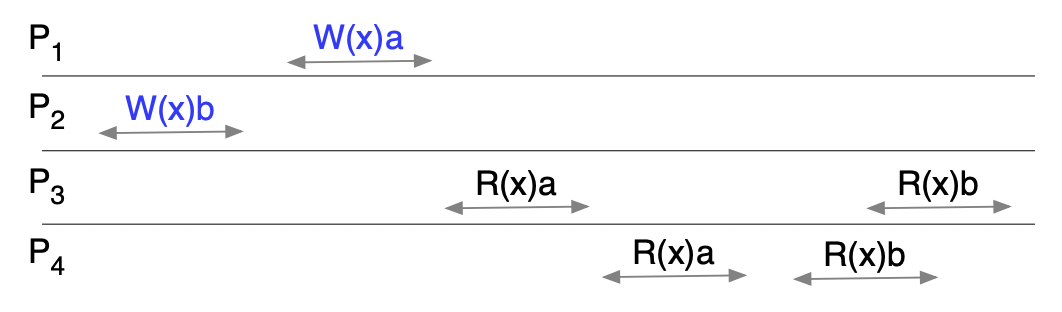
该情况与情况 1 相同,满足顺序一致性的,顺序之一的 为
1 | P1:W(x)a -> P3:R(x)a -> P4:R(x)a -> P2:W(x)b -> P3:R(x)b -> P4:R(x)b |
情况 3:
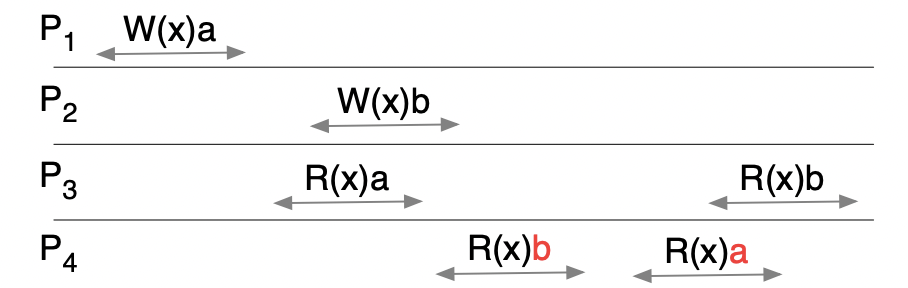
该情况不满足顺序一致性,因为图中的 进程和 进程的执行顺序不同,不满足条件 1。(不存在顺序 条件同时满足条件 1 和 2)
- 进程中
P3:R(x)a -> P3:R(x)b - 进程中
P4:R(x)b -> P4:R(x)a
伪算法表述
顺序一致性不如线性那么严格,相比线性更容易实现。虽然存在全局顺序,但是本地处理器执行操作顺序未必一定要严格遵守全局时间顺序。整个过程只需要对写操作使用全序广播机制。
在简化的算法中,并不需要对读操作使用全序广播。因为:
- 因不使用流水线,相同处理器内部执行的连续操作顺序不变
- 读操作在不同处理器之间相互独立,其顺序只与相应写操作执行顺序相关。
(1) 本地读算法
1 | int : x; |
在该算法中,本地写操作完成有延迟(等待广播 - 第6行)。该算法适合在读频繁的应用中使用。
(2) 本地写算法
1 | int : x; |
在该算法中,本地写操作需要立即执行获得响应。该算法适合在写频繁的应用中使用。
线性一致性
线性一致性要求首先满足顺序一致性的条件,同时还多了一个条件,不妨称之为条件 3:
- 条件 3:不同进程的事件,如果在时间上不重叠,即不是并发事件,那么要求这个先后顺序在重排之后保持一致。即 ,那么
我们重新考虑顺序一致性中的【例2】:
情况 1:

该情况满足顺序一致性的,顺序之一的 为
1 | P1:W(x)a -> P3:R(x)a -> P4:R(x)a -> P2:W(x)b -> P3:R(x)b -> P4:R(x)b |
在此基础上,该序列还满足线性一致性。
情况 2:

该情况与情况 1 相同,满足顺序一致性的,顺序之一的 为
1 | P1:W(x)a -> P3:R(x)a -> P4:R(x)a -> P2:W(x)b -> P3:R(x)b -> P4:R(x)b |
但是其不满足线性一致性,因为 进程开始于 R(x)a,但是全局的序列开始于 W(x)b。
顺序一致性和线性一致性总结
可以看到,如果满足线性一致性,就一定满足顺序一致性,因为后者的条件是前者的真子集。
除了满足这些条件以外,这两个一致性还有一个要求:系统中所有进程的顺序是一致的,即如果系统中的进程 A 按照要求使用了某一种排序,即便有其他排序的可能性存在,系统中的其他进程也必须使用这种排序,系统中只能用一种满足要求的排序。
这个要求,使得满足顺序和线性一致性的系统,对外看起来“表现得像只有一个副本”一样。
但因果一致性则与此不同:只要满足因果一致性的条件,即便不同进程的事件排列不一致也没有关系。
因果一致性
相较于顺序和线性一致性,因果一致性就简单一些,其实就只要满足在 Lamport 时钟中提到的 happen-before 关系即可:
-
引入符号 做为表示事件之间
happen-before的记号。 -
在同一个进程中,如果事件 在事件 之前发生,那么。 (进程每次发出事件之后都会将本地的 lamport 时钟加一,于是可以在同一个进程内定义事件的先后顺序了)
-
在不同的进程中,如果事件 表示一个进程发出一个事件,事件 表示接收进程收到这个事件,那么也必然满足 。(接收进程在收到事件之后会取本地时钟和事件时钟的最大值并且+1,于是发出事件和接收事件尽管在不同的进程,但是也可以比较其 lamport 时钟知道其先后顺序了)
-
最后,
happend-before关系是满足传递性的,即:如果 且 ,那么也一定有 。
同样的,我们使用一个评论朋友圈的例子来解释因果一致性:
- 评论另一个用户的评论:相当于进程给另一个进程发消息,肯定要求满足
happen-before关系,即先有了评论,才能针对这个评论发表评论。 - 同一个用户的评论:相当于同一个进程的事件,也是必须满足
happen-before关系才行。
【情况 1】:我们将以下场景抽象为模型,即如下图所示
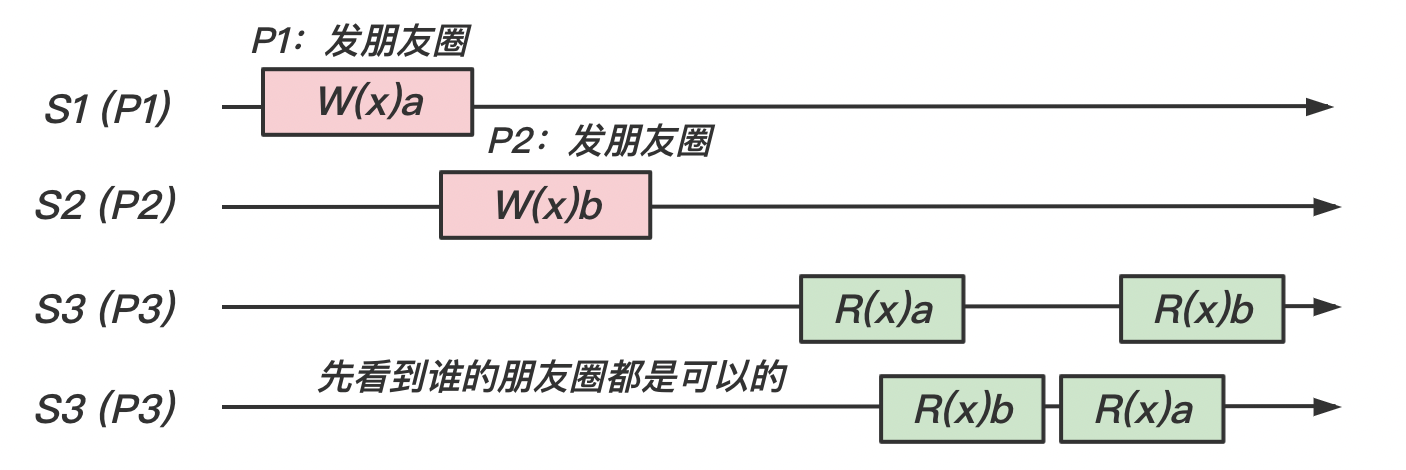
在这个模型中,存在 happen-before 关系的时间有 W(x)a -> R(x)a 和 W(x)b -> R(x)b。所以在这个情况下是满足因果一致性的。
【情况 2】:我们在上一个例子的上做一些修改。 不再发朋友圈,而是看到了 的朋友圈后对其评论,即 R(x)a -> W(x)b。如下图