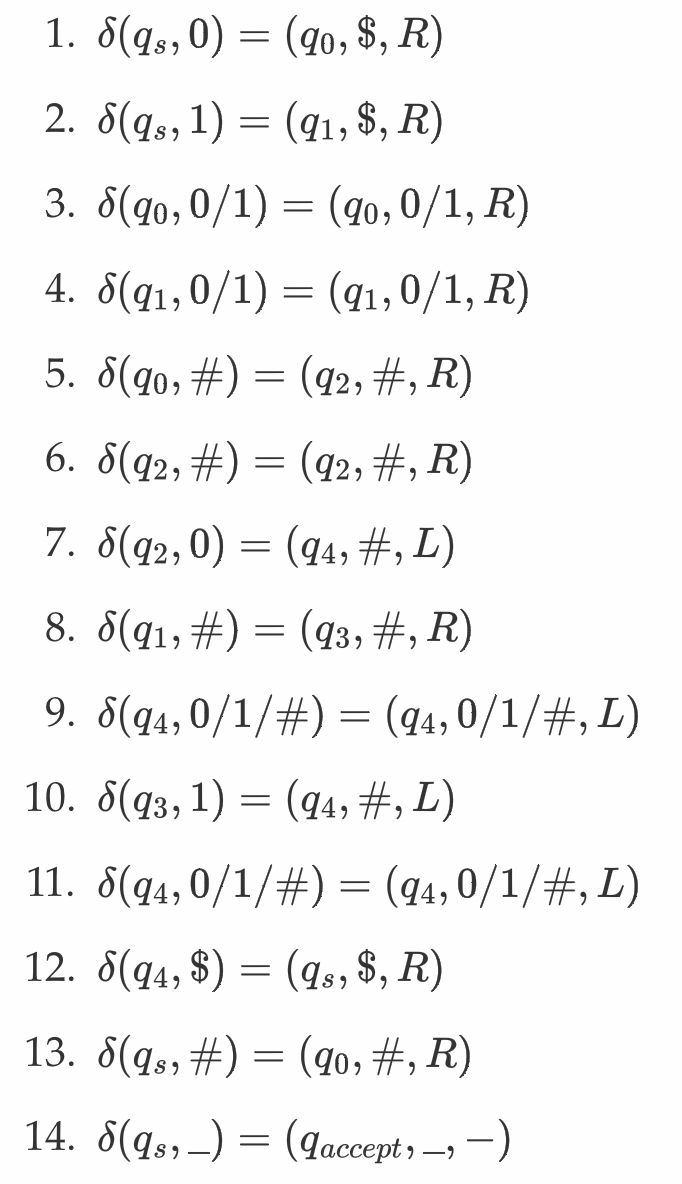本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第八学期课程 “Calculabilité et Complexité” 总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考:
我们在研究一个问题的复杂度之前,首先需要研究这个问题能否使用计算机解决(可计算性)。
什么是问题?
函数问题:给定一个字符串 Σ ∗ \Sigma_* Σ ∗ f f f Σ ∗ \Sigma_* Σ ∗
f : Σ ∗ → Σ ∗ f: \Sigma_* \to \Sigma_*
f : Σ ∗ → Σ ∗
决策问题:给定一个字符串 Σ ∗ \Sigma_* Σ ∗ { y e s = 1 , n o = 0 } \{_{yes} = 1,\quad _{no} = 0\} { y e s = 1 , n o = 0 }
f : Σ ∗ → { y e s = 1 , n o = 0 } f: \Sigma_* \to \{_{yes} = 1,\quad _{no} = 0\}
f : Σ ∗ → { y e s = 1 , n o = 0 }
实际上可以将字符串集合 Σ ∗ \Sigma_* Σ ∗
图灵机是一个虚拟的机器,由数学家阿兰·图灵1936年提出来的,尽管这个机器很简单,但它可以模拟计算机的任何算法,无论这个算法有多复杂。
图灵机实际上是解决一个具体问题的程序(算法)
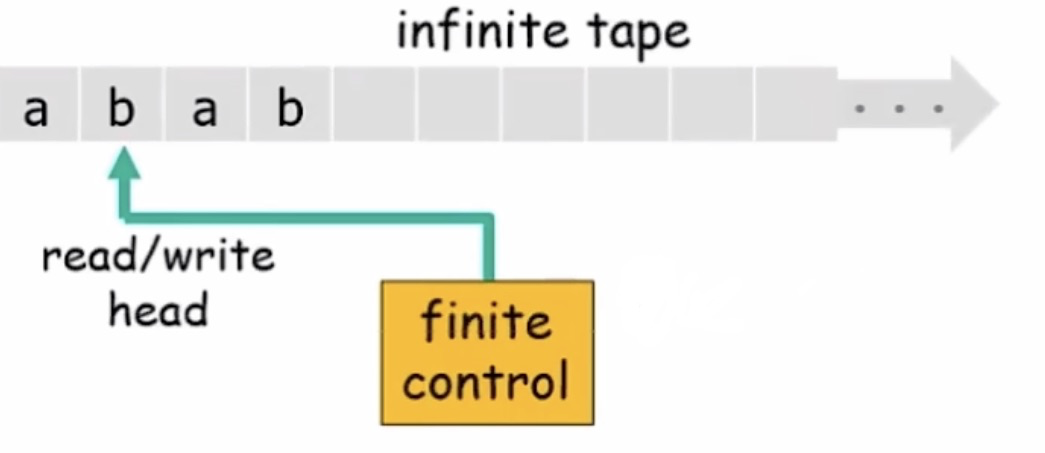
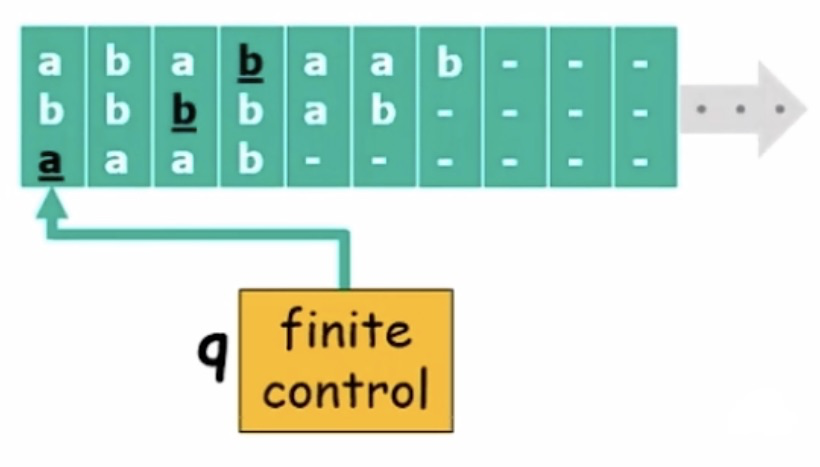
上面是一个图灵机的简单示意图。
有限控制器:所谓有限是指该,控制器不随输入的长度变化而变化。对应计算机的CPU
无穷的纸带:纸带就像一个计算机的存储器一样。纸带上面的每个格子是空白的,但是可以读写数据
读写头:可以向纸带读取或写入数据的指针
可以用如下六元组定义该图灵机
M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩ \mathcal{M} = ⟨Q,\Sigma,\delta,q_s,q_{accept},q_{reject}⟩
M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩
Q Q Q
Σ \Sigma Σ Σ = { 0 , 1 } \Sigma = \{0,1\} Σ = { 0 , 1 }
δ \delta δ
δ : Q × Σ → Q × Σ × { L , R , − } \delta : Q \times \Sigma \to Q \times \Sigma \times \{L,R,-\}
δ : Q × Σ → Q × Σ × { L , R , − }
输入:当时的状态 Q Q Q Σ \Sigma Σ
输出:函数变化后的状态 Q Q Q Σ \Sigma Σ
q s ∈ Q q_s \in Q q s ∈ Q
q a c c e p t ∈ Q q_{accept} \in Q q a c c e p t ∈ Q
q r e j e c t ∈ Q q_{reject} \in Q q r e j e c t ∈ Q
【例】
创建一个图灵机以满足
输入:X # Y : X , Y ∈ { 二 进 制 数 } : X,Y \in \{二进制数\} : X , Y ∈ { 二 进 制 数 }
输出:当 X = Y X = Y X = Y
M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩ \mathcal{M} = ⟨Q,\Sigma,\delta,q_s,q_{accept},q_{reject}⟩ M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩ Q = { q s , q 0 , q 1 , q 2 , q 3 , q 4 , q a c c e p t , q r e j e c t } Q = \{ q_s, q_0, q_1, q_2, q_3, q_4, q_{accept}, q_{reject}\} Q = { q s , q 0 , q 1 , q 2 , q 3 , q 4 , q a c c e p t , q r e j e c t } Σ = \Sigma = Σ = δ ( Q , Σ ) = ( Q , Σ , { L , R , − } ) \delta (Q, \Sigma) = (Q, \Sigma, \{L,R,-\}) δ ( Q , Σ ) = ( Q , Σ , { L , R , − } )
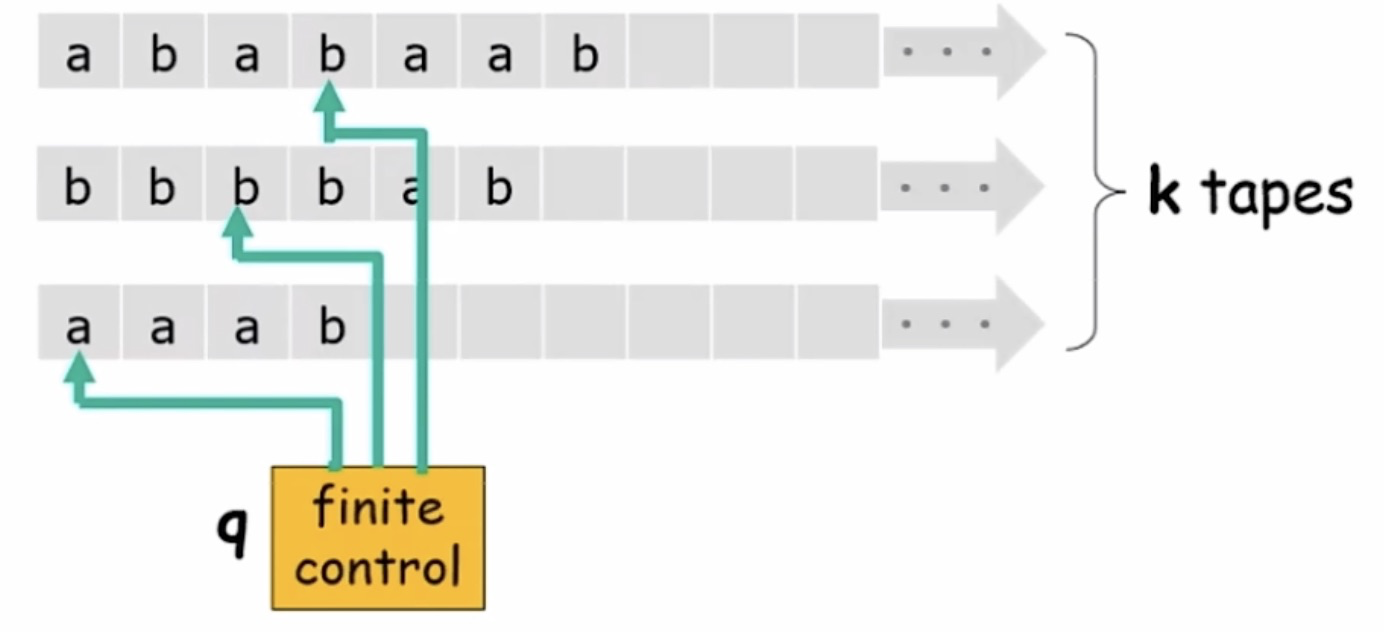
也可以用如下六元组定义该图灵机
M = ⟨ Q , Σ k , δ , q s , q a c c e p t , q r e j e c t ⟩ \mathcal{M} = ⟨Q,\Sigma^k,\delta,q_s,q_{accept},q_{reject}⟩
M = ⟨ Q , Σ k , δ , q s , q a c c e p t , q r e j e c t ⟩
Q Q Q
Σ \Sigma Σ
δ \delta δ
δ : Q × Σ k → Q × Σ k × { L , R , − } k \delta : Q \times \Sigma^k \to Q \times \Sigma^k \times \{L,R,-\}^k
δ : Q × Σ k → Q × Σ k × { L , R , − } k
q s ∈ Q q_s \in Q q s ∈ Q
q a c c e p t ∈ Q q_{accept} \in Q q a c c e p t ∈ Q
q r e j e c t ∈ Q q_{reject} \in Q q r e j e c t ∈ Q
上述的多纸带图灵机可以组合成如下的单纸带图灵机
可以引入符号 x ‾ \underline{x} x
遍历整个纸带。O ( t ( n ) ) O(t(n)) O ( t ( n ) )
找到符号 x ‾ \underline{x} x O ( t ( n ) ) × O ( t ( n ) ) O(t(n)) \times O(t(n)) O ( t ( n ) ) × O ( t ( n ) )
Everything we can compute on a physical computer can be comptued on a Turing Machine.
所有的计算模型能做的事情都是一样的,没有任何一个模型能力比图灵机强,只是时间快慢不同。
图 灵 机 = 任 何 计 算 机 上 的 程 序 = 算 法 图灵机 = 任何计算机上的程序 = 算法
图 灵 机 = 任 何 计 算 机 上 的 程 序 = 算 法
根据 Church 公理,我们想要研究一个问题是否是可计算的,我们只需要研究在图灵机上的可计算性。
一个语言 L \mathcal{L} L M \mathcal{M} M L \mathcal{L} L M \mathcal{M} M L \mathcal{L} L M \mathcal{M} M 不停机 。
而一个语言 L ′ \mathcal{L'} L ′ M ′ \mathcal{M'} M ′ L \mathcal{L} L M \mathcal{M} M L \mathcal{L} L M \mathcal{M} M
Definition
An algorithm (or a program or a Turing Machine) A \mathcal{A} A Q Q Q x x x A ( x ) \mathcal{A}(x) A ( x )
一个算法 A \mathcal{A} A Q Q Q
一个问题 Q Q Q A \mathcal{A} A
停机问题就是判断任意一个程序是否会在有限的时间之内结束运行的问题。
该问题等价于如下的判定问题:给定一个算法 A \mathcal{A} A w w w A \mathcal{A} A w w w
该问题不是可解的 (not solvable),即不存在一个算法 A \mathcal{A} A A ′ \mathcal{A'} A ′ A \mathcal{A} A
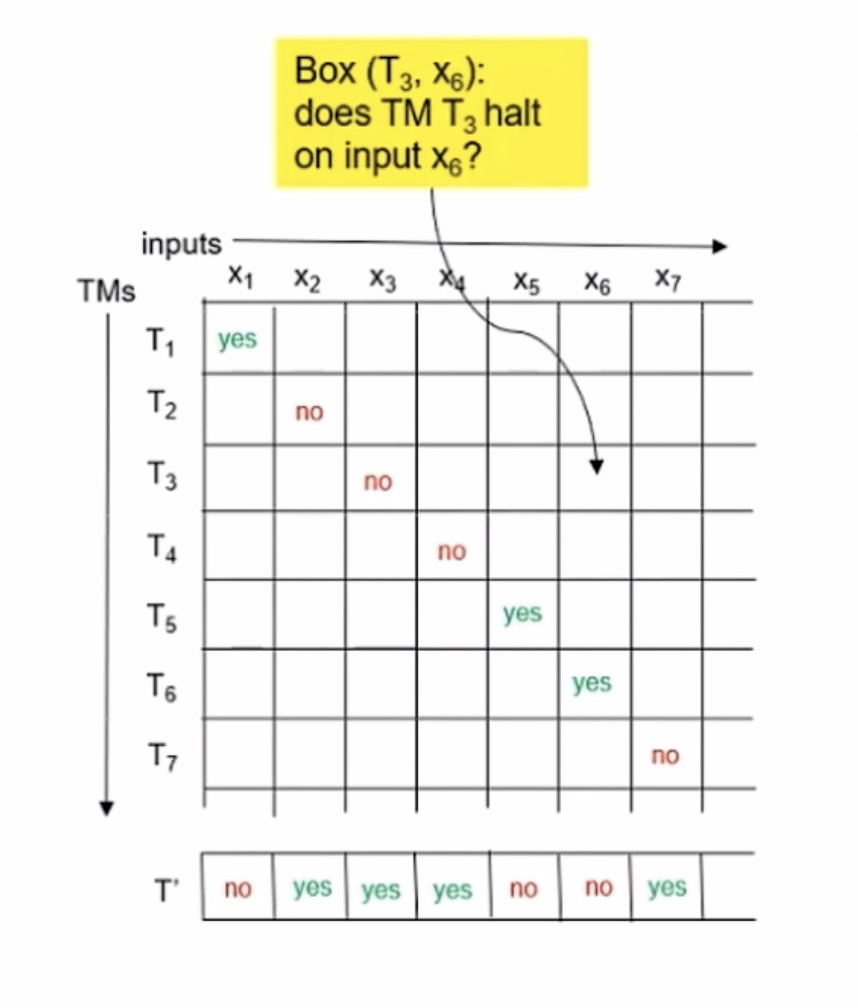
对角化(Diagonalization)
在上图中,所有的图灵机集合 T M s \mathcal{TMs} T M s i n p u t s inputs i n p u t s M i \mathcal{M}_i M i x j x_j x j
我们假设存在一个图灵机 M \mathcal{M} M M ′ \mathcal{M'} M ′ x i x_i x i M \mathcal{M} M M ( M ′ i , x i ) \mathcal{M}(\mathcal{M'}_i, \; x_i) M ( M ′ i , x i )
⚠️ 请注意区分图灵机 M \mathcal{M} M M ’ \mathcal{M’} M ’
因为图灵机 M ∗ \mathcal{M}^{*} M ∗ M i \mathcal{M}_{i} M i
所以图灵机 M ∗ \mathcal{M}^{*} M ∗ T M s \mathcal{TMs} T M s
我们仍然假设存在一个图灵机 M \mathcal{M} M M ′ \mathcal{M'} M ′ x x x M \mathcal{M} M
M ( M ′ , x ) = { a c c e p t if M ′ halts on x r e j e c t otherwise \mathcal{M}(\mathcal{M'},x) = \begin{cases}
accept \quad \text{if } \mathcal{M'} \text{ halts on } x \\
reject \quad \text{otherwise}
\end{cases}
M ( M ′ , x ) = { a c c e p t if M ′ halts on x r e j e c t otherwise
我们考虑如下自我停机问题:
M ( M , x ) \mathcal{M}(\mathcal{M},x)
M ( M , x )
后略。
Definition
令 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Q 1 ≤ Q 2 Q_1 \le Q_2 Q 1 ≤ Q 2 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 A \mathcal{A} A x x x A ( x ) \mathcal{A}(x) A ( x ) Q 1 Q_1 Q 1 A ( x ) \mathcal{A}(x) A ( x ) Q 2 Q_2 Q 2
Lemma
如果 Q 2 Q_2 Q 2 Q 1 Q_1 Q 1
如果 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2
输入:图灵机 M \mathcal{M} M
问题:图灵机 M \mathcal{M} M i n p u t s inputs i n p u t s
Q H a l t i n g ≤ Q A c c p e t − A l l Q_{Halting} \le Q_{Accpet-All}
Q H a l t i n g ≤ Q A c c p e t − A l l
所以全接受问题也是不可解的
输入:两个图灵机 M 1 \mathcal{M}_1 M 1 M 2 \mathcal{M}_2 M 2
问题: M 1 \mathcal{M}_1 M 1 M 2 \mathcal{M}_2 M 2
我们已知停机问题是不可解的,全接受问题也是不可解的。
我们假设一种特殊情况,即图灵机 M 0 \mathcal{M}_0 M 0 i n p u t s inputs i n p u t s
Q A c c p e t − A l l ( M ) ≤ Q P r o g − E q u ( M , M 0 ) Q_{Accpet-All}(\mathcal{M}) \le Q_{Prog-Equ}(\mathcal{M}, \mathcal{M_0})
Q A c c p e t − A l l ( M ) ≤ Q P r o g − E q u ( M , M 0 )
如果图灵机 M \mathcal{M} M M \mathcal{M} M M 0 \mathcal{M}_0 M 0
如果图灵机 M \mathcal{M} M M \mathcal{M} M M 0 \mathcal{M}_0 M 0
而全接受问题是不可解的,所以等价程序问题也是不可解的。
Everything we can compute in time t ( n ) t(n) t ( n ) (in space O ( s ( n ) ) O(s(n)) O ( s ( n ) ) ) on a physical computer can be comptued on a 1-tape Turing Machine in time t O ( 1 ) ( n ) t^{O(1)}(n) t O ( 1 ) ( n ) (in space O ( s ( n ) ) O(s(n)) O ( s ( n ) ) .
如果在计算机上做某一件事所花费的时间是 t ( n ) t(n) t ( n ) O ( s ( n ) ) O(s(n)) O ( s ( n ) ) t O ( 1 ) ( n ) t^{O(1)}(n) t O ( 1 ) ( n ) O ( s ( n ) ) O(s(n)) O ( s ( n ) )
复杂性理论所研究的资源中最常见的是时间(要通过多少步演算才能解决问题)和空间(在解决问题时需要多少内存)。
T I M E ( t ( n ) ) TIME(t(n)) T I M E ( t ( n ) ) 是指在计算机科学与工程领域完成一个算法所需要的时间,是衡量一个算法优劣的重要参数。时间复杂度越小,说明该算法效率越高,则该算法越有价值。
D T I M E DT_{IME} D T I M E 对于一个【确定性】的图灵机,我们可以给出其常见的几种 【(确定的)时间复杂度 D T I M E DT_{IME} D T I M E
P \mathcal{P} P D T I M E DT_{IME} D T I M E
Definition
P ≜ ⋃ k ∈ N D T I M E ( n k ) \mathcal{P} \triangleq \bigcup_{k \in \mathbb{N}} DT_{IME}(n^k)
P ≜ k ∈ N ⋃ D T I M E ( n k )
即 P \mathcal{P} P 【确定性】图灵机 的多项式时间复杂度 ,P \mathcal{P} P P \mathcal{P} P
E T I M E \mathsf{ETIME} E T I M E
E T I M E ≜ ⋃ k ∈ N D T I M E ( 2 k n ) \mathsf{ETIME} \triangleq \bigcup_{k \in \mathbb{N}} DT_{IME}(2^{kn})
E T I M E ≜ k ∈ N ⋃ D T I M E ( 2 k n )
E X P T I M E \mathsf{EXPTIME} E X P T I M E
E X P T I M E ≜ ⋃ k ∈ N D T I M E ( 2 n k ) \mathsf{EXPTIME} \triangleq \bigcup_{k \in \mathbb{N}} DT_{IME}(2^{n^k})
E X P T I M E ≜ k ∈ N ⋃ D T I M E ( 2 n k )
结论
P ⊊ E T I M E ⊊ E X P T I M E \mathcal{P} \subsetneq \mathsf{ETIME} \subsetneq \mathsf{EXPTIME}
P ⊊ E T I M E ⊊ E X P T I M E
P \mathcal{P} P 包含在但不等于 E T I M E ET_{IME} E T I M E 包含在但不等于 E X P T I M E \mathsf{EXPTIME} E X P T I M E
N T I M E NT_{IME} N T I M E 将在 非确定性 章节讨论。
对于一个决策性问题 L \mathcal{L} L
写一个可以解决问题 L \mathcal{L} L
证明这个程序是最优的(目前学界并没有数学上严格的证明)
为了尽量满足要求 2 ,我们做出了如下妥协措施:
我们引入了【规约 (reductions) 】来比较问题的难度
我们依照【完整性 (completeness) 】来找出难问题
之前我们讲到的图灵机,实际上是在模拟人类的思考方式。
对于一个图灵机 M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩ \mathcal{M} = ⟨Q,\Sigma,\delta,q_s,q_{accept},q_{reject}⟩ M = ⟨ Q , Σ , δ , q s , q a c c e p t , q r e j e c t ⟩ 唯一一个确定的 δ \delta δ 将当前状态转变为下一状态:δ ( q 0 , a 0 ) = ( q 1 , a 1 , { L , R , − } ) \delta (q_0, a_0) = (q_1, a_1, \{L,R,-\}) δ ( q 0 , a 0 ) = ( q 1 , a 1 , { L , R , − } )
但是人类的思考具有不确定性(所谓“突发灵感”),但是图灵机无法模拟这种不确定性行为。
我们希望计算机也有这种特性,即每当计算机面临选择时,我们将不同的选择列出,而让计算机选择一种“最好”的方式执行。
譬如当我们在下棋时,我们经常没办法具体解释落子的原因,我们希望计算机可以选择一种“最好”的方式执行。
回顾 带权图的最短路径问题 :
给定一个带权图 G G G s s s t t t k k k s − t s-t s − t ≤ k \le k ≤ k
1 2 3 4 5 6 7 8 9 10 11 12 v_0 = s; for (i=1 ; i<=h; i++) for (j=1 ; j<=h; j++) {ok1 = check [v[i-1 ], v[i]] is an edge} ok2 = check (v_h == t); ok3 = check (sum(weight(v[i], v[i+1 ])) <= k); ok = (ok1 && ok2 && ok3) if (ok) return 'no' else return 'yes'
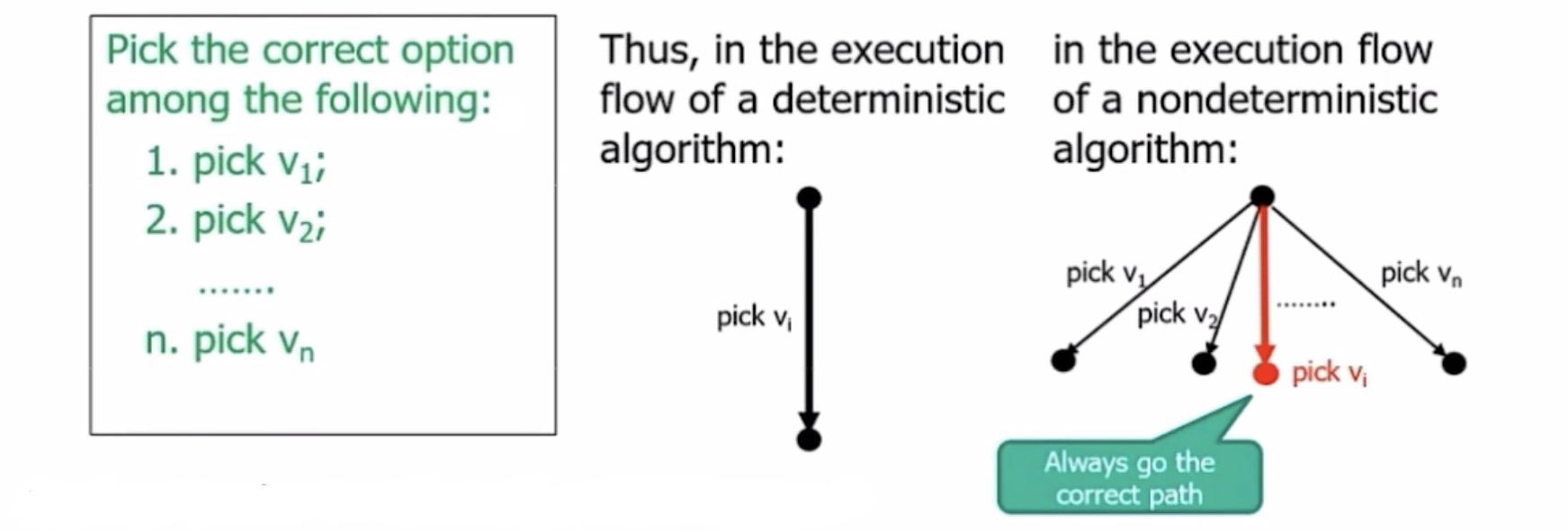
那么计算机如何"神奇地"找到一个最优的顶点 v i v_i v i
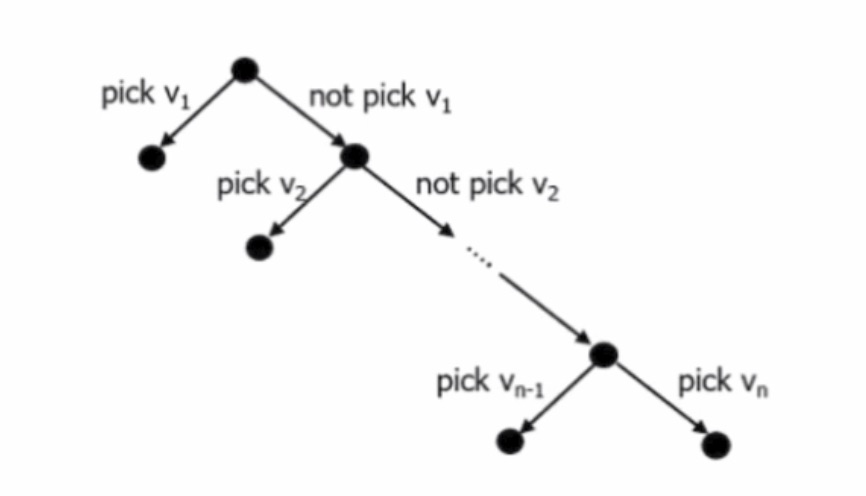
或用二叉树表示(非确定性图灵机面临的选择不超过两个):
⚠️注意:这里并不是“计算机遍历所有分支然后选择一条最优路径”而是“我们的计算机有一种特殊的能力,可以直接选择一个最优路径”。
对于一个【确定性】的图灵机:
δ ( q 0 , a 0 ) = ( q 1 , a 1 , V 1 ) (是唯一且确定的) \begin{aligned}
& \delta (q_0, a_0) = (q_1, a_1, V_1) \\
& \text{(是唯一且确定的)}
\end{aligned}
δ ( q 0 , a 0 ) = ( q 1 , a 1 , V 1 ) ( 是唯一且确定的 )
对于一个【非确定性】的图灵机:
δ ( q 0 , a 0 ) = ( q 1 , a 1 , V 1 ) δ ( q 0 , a 0 ) = ( q 2 , a 2 , V 2 ) . . . δ ( q i , a i ) = ( q i , a i , V i ) , i ∈ C (不是唯一且确定的) \begin{aligned}
& \delta (q_0, a_0) = (q_1, a_1, V_1) \\
& \delta (q_0, a_0) = (q_2, a_2, V_2)\\
& ... \\
& \delta (q_i, a_i) = (q_i, a_i, V_i), i \in C\\
& \text{(不是唯一且确定的)}
\end{aligned}
δ ( q 0 , a 0 ) = ( q 1 , a 1 , V 1 ) δ ( q 0 , a 0 ) = ( q 2 , a 2 , V 2 ) . . . δ ( q i , a i ) = ( q i , a i , V i ) , i ∈ C ( 不是唯一且确定的 )
Theorem.
在不考虑时间因素的前提下(有效时间*),一个“有神秘能力的”计算机能做的事也可以 在一个“没有神秘能力的”计算机上解决。
而在考虑时间因素下(有效时间*),一个“有神秘能力的”计算机能做的事 有时可以 在一个“没有神秘能力的”计算机上解决 (UNKNOWN)。
【*有效时间】是多项式时间,即算法的运行时间是 O ( n c ) O(n^c) O ( n c ) c c c
N T I M E NT_{IME} N T I M E
N P \mathcal{NP} N P
N P ≜ ⋃ k ∈ N N T I M E ( n k ) \mathcal{NP} \triangleq \bigcup_{k \in \mathbb{N}} NT_{IME}(n^k)
N P ≜ k ∈ N ⋃ N T I M E ( n k )
即 N P \mathcal{NP} N P 【非确定性】图灵机 的多项式时间复杂度 。
N E X P T I M E \mathsf{NEXPTIME} N E X P T I M E
N E X P T I M E ≜ ⋃ k ∈ N N T I M E ( 2 k n ) \mathsf{NEXPTIME} \triangleq \bigcup_{k \in \mathbb{N}} NT_{IME}(2^{kn})
N E X P T I M E ≜ k ∈ N ⋃ N T I M E ( 2 k n )
结论
P ⊆ N P ⊆ E X P T I M E ⊆ N E X P T I M E \mathcal{P} \; \subseteq \; \mathcal{NP} \; \subseteq \; \mathsf{EXPTIME} \; \subseteq \; \mathsf{NEXPTIME}
P ⊆ N P ⊆ E X P T I M E ⊆ N E X P T I M E
P ⊊ E X P T I M E N P ⊊ N E X P T I M E \mathcal{P} \; \subsetneq \; \mathsf{EXPTIME} \qquad \mathcal{NP} \; \subsetneq \; \mathsf{NEXPTIME}
P ⊊ E X P T I M E N P ⊊ N E X P T I M E
P = ? N P \mathcal{P} \overset{\underset{\mathrm{?}}{}}{=} \mathcal{NP}
P = ? N P
N P = ? E X P T I M E \mathcal{NP} \overset{\underset{\mathrm{?}}{}}{=} \mathsf{EXPTIME}
N P = ? E X P T I M E
E X P T I M E = ? N E X P T I M E EXPT_{IME} \overset{\underset{\mathrm{?}}{}}{=} \mathsf{NEXPTIME}
E X P T I M E = ? N E X P T I M E
P = ? N P \mathcal{P} \overset{\underset{\mathrm{?}}{}}{=} \mathcal{NP} P = ? N P
在有效时间下,一个“有神秘能力的”计算机能做的事是否可以在一个“没有神秘能力的”计算机上解决?
等价于
一个(判断性)问题如果在【非确定性图灵机】上有效时间内可解,该问题是否可以在一个【确定性图灵机】上有效时间内可解?
等价于
P = ? N P \mathcal{P} \overset{\underset{\mathrm{?}}{}}{=} \mathcal{NP}
P = ? N P
P P P N P NP N P
P \mathcal{P} P N P \mathcal{NP} N P
P \mathcal{P} P P \mathcal{P} P
the class of (decision) problems that can be solved by polynomial-time [nondeterministic] algorithms(Turing Machines)
N P \mathcal{NP} N P
the class of (decision) problems that can be solved by polynomial-time [deterministic] algorithms(Turing Machines)
以下推论 都是等价的
一个“没有神秘能力的”计算机能做的事可以在一个“有神秘能力的”计算机上解决
在【非确定性图灵机】上可以做【确定性图灵机】能做的事
【确定性图灵机】不会比【非确定性图灵机】更强
所有属于 P \mathcal{P} P N P \mathcal{NP} N P
P ⊆ N P ① \mathcal{P} \subseteq \mathcal{NP} \qquad \text{①}
P ⊆ N P ①
反言之,如果:
一个“有神秘能力的”计算机能做的事可以在一个“没有神秘能力的”计算机上解决
在【确定性图灵机】上可以做【非确定性图灵机】能做的事
所有属于 N P \mathcal{NP} N P P \mathcal{P} P
N P ⊆ P ② \mathcal{NP} \subseteq \mathcal{P} \qquad \text{②}
N P ⊆ P ②
如果满足以上两点,我们可以推出:
① + ② ⇒ P = N P 无人可知是否成立 {① + ②} \quad \Rightarrow \quad \mathcal{P} = \mathcal{NP} \quad \text{无人可知是否成立}
① + ② ⇒ P = N P 无人可知是否成立
P = N P \mathcal{P} = \mathcal{NP} P = N P
优点:很多工程上很重要的优化问题都可以用计算机解决
缺点:所有的密码系统都会被破解
在有权图 G G G ≤ k \le k ≤ k
1 2 3 4 5 6 7 8 9 1. for (i=1 ; i<=n; i++) 2. check that all vertices picked in step1 are different;3. for (i=1 ; i<=n-1 ; i++){ check [v[i], v[i+1 ]] is an edge;} 4. check (sum(weight(v[i], v[i+1 ])) <= k);5. if (any test in steps 2 -4 fails) then return ('no' ) else return ('yes' )
给定一个合取范式 F F F F F F F = 1 F = 1 F = 1
即找到一组 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X = x 1 , x 2 , x 3 , . . . , x n F = 1 F = 1 F = 1
F = ( ¬ x 1 ∨ x 2 ∨ x 5 ∨ ¬ x 4 ) ∧ ( x 1 ∨ x 6 ∨ x 5 ∨ x 4 ) ∧ ( ¬ x 5 ∨ x 4 ∨ ¬ x 2 ) ∧ ( x 3 ∨ ¬ x 4 ) ∧ ( x 1 ∨ ¬ x 3 ∨ x 6 ) \begin{aligned}
F =
& \quad (\neg x_1 \lor x_2 \lor x_5 \lor \neg x_4)\\
& \land (x_1 \lor x_6 \lor x_5 \lor x_4)\\
& \land (\neg x_5 \lor x_4 \lor \neg x_2)\\
& \land (x_3 \lor \neg x_4)\\
& \land (x_1 \lor \neg x_3 \lor x_6)\\
\end{aligned}
F = ( ¬ x 1 ∨ x 2 ∨ x 5 ∨ ¬ x 4 ) ∧ ( x 1 ∨ x 6 ∨ x 5 ∨ x 4 ) ∧ ( ¬ x 5 ∨ x 4 ∨ ¬ x 2 ) ∧ ( x 3 ∨ ¬ x 4 ) ∧ ( x 1 ∨ ¬ x 3 ∨ x 6 )
1 2 3 4 5 1. for (each variable x_i in F) 2. if (the assignment constructed in step1 makes F=1 ) then return ('yes' ) else return ('no' )
我们假设有两个机器 M 1 , M 2 M_1, M_2 M 1 , M 2 n n n T T T t 1 , t 2 , t 3 , . . . , t n t_1, t_2, t_3, ..., t_n t 1 , t 2 , t 3 , . . . , t n n n n
1 2 3 4 5 1. for (each job t_i) 2. if (according by step1, both machines M1 and M2 can finish no later than time T) then return ('yes' ) else return ('no' )
给定一个图 G G G G G G k k k
1 2 3 4 5 6 7 8 1. for (i=1 ; i<=k; i++){ } 2. check (all the vertices picked in step1 are different)3. check (no two vertices picked in step1 are adjacent 邻接的)4. if (any check in step2 and step3 fails) then return ('no' ) else return ('yes' )
⇔ \Leftrightarrow ⇔ 给定一个合取范式 F F F F F F F = 1 F = 1 F = 1
F = ( ¬ x 1 ∨ x 2 ∨ x 5 ∨ ¬ x 4 ) ∧ ( x 1 ∨ x 6 ∨ x 5 ∨ x 4 ) ∧ ( ¬ x 5 ∨ x 4 ∨ ¬ x 2 ) ∧ ( x 3 ∨ ¬ x 4 ) ∧ ( x 1 ∨ ¬ x 3 ∨ x 6 ) \begin{aligned}
F =
& \quad (\neg x_1 \lor x_2 \lor x_5 \lor \neg x_4)\\
& \land (x_1 \lor x_6 \lor x_5 \lor x_4)\\
& \land (\neg x_5 \lor x_4 \lor \neg x_2)\\
& \land (x_3 \lor \neg x_4)\\
& \land (x_1 \lor \neg x_3 \lor x_6)\\
\end{aligned}
F = ( ¬ x 1 ∨ x 2 ∨ x 5 ∨ ¬ x 4 ) ∧ ( x 1 ∨ x 6 ∨ x 5 ∨ x 4 ) ∧ ( ¬ x 5 ∨ x 4 ∨ ¬ x 2 ) ∧ ( x 3 ∨ ¬ x 4 ) ∧ ( x 1 ∨ ¬ x 3 ∨ x 6 )
给定一个图 G G G G G G k k k
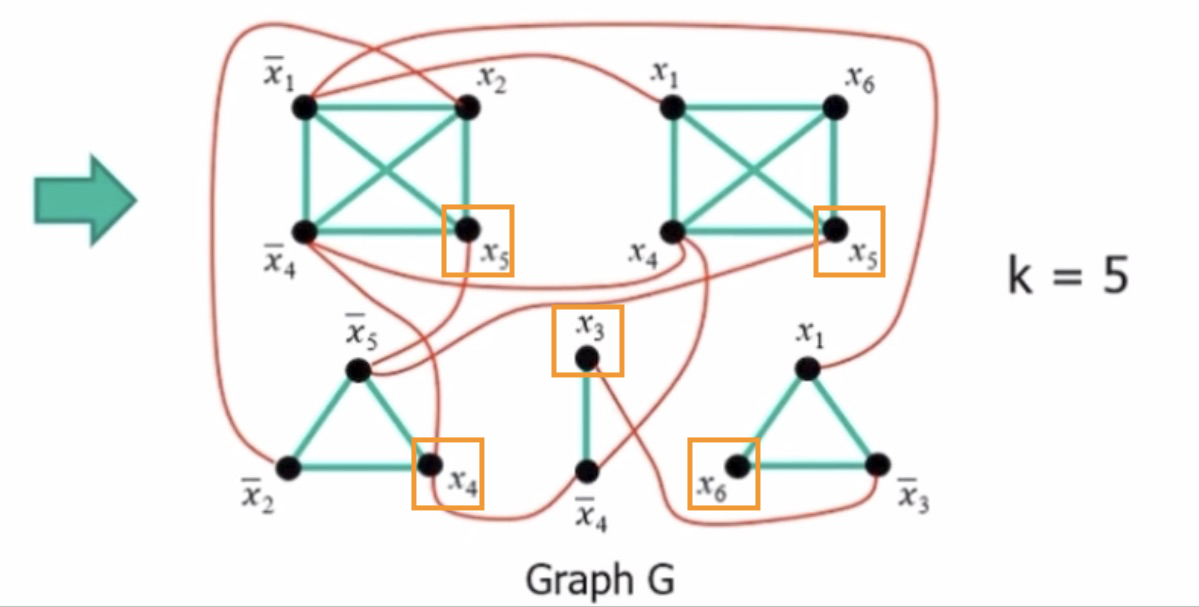
在 SAT 问题中,对于每一个合取的每一个子句(即每一行括号内的元素),我们都可以用一个【完全图】来表示。
不同子句之间的相通元素若互为“非”的关系,则我们将其连接起来。
例如第一个子句中的 ¬ x 1 \neg x_1 ¬ x 1 x 1 x_1 x 1
k = 子 句 的 个 数 k = 子句的个数 k = 子 句 的 个 数
如果我们可以在图 G G G k k k
等价于
存在一组 X = x 1 , x 2 , x 3 , . . . , x n X={x_1,x_2,x_3,...,x_n} X = x 1 , x 2 , x 3 , . . . , x n F = 1 F = 1 F = 1
至此,我们就将“可满足性 (SAT) 问题”转化成了“独立集问题”
因此,如果一个独立集问题属于 P \mathcal{P} P
Definition
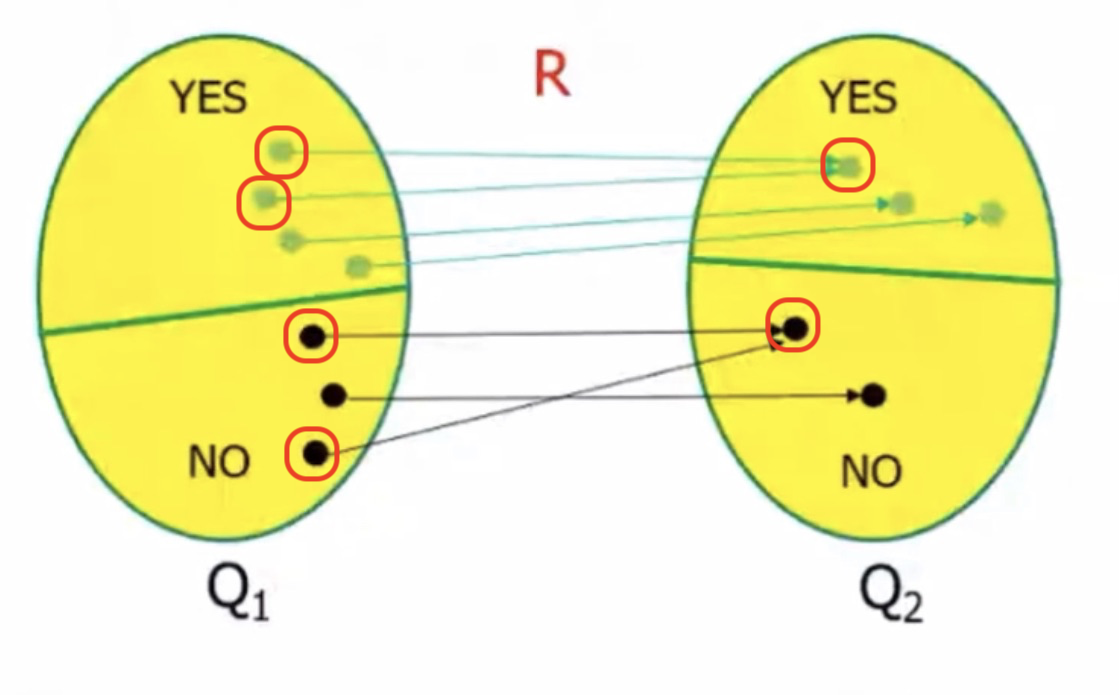
我们有两个决策性问题 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 R \mathcal{R} R Q 1 Q_1 Q 1 x 1 x_1 x 1 Q 2 Q_2 Q 2 x 2 x_2 x 2 x 1 x_1 x 1 Q 1 Q_1 Q 1 x 2 x_2 x 2 Q 2 Q_2 Q 2
一个决策性问题 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Q 1 ≤ m p Q 2 Q_1 \le^{p}_{m} Q_2 Q 1 ≤ m p Q 2 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Q 2 Q_2 Q 2 Q 1 Q_1 Q 1
x 1 : Q 1 的 实 例 → p o l y − t i m e R x 2 : Q 2 的 实 例 x_1:Q_1的实例 \quad \xrightarrow[poly-time]{\mathcal{R}} \quad x_2:Q_2的实例
x 1 : Q 1 的 实 例 R p o l y − t i m e x 2 : Q 2 的 实 例
⚠️注意:这里的“实例 x x x Q Q Q
性质
如果 Q 1 ≤ m p Q 2 Q_1 \le^{p}_{m} Q_2 Q 1 ≤ m p Q 2 Q 2 Q_2 Q 2 P \mathcal{P} P Q 1 Q_1 Q 1 P \mathcal{P} P
如果 Q 1 ≤ m p Q 2 Q_1 \le^{p}_{m} Q_2 Q 1 ≤ m p Q 2 Q 2 Q_2 Q 2 不 属于 P \mathcal{P} P Q 1 Q_1 Q 1 不 属于 P \mathcal{P} P
规约具有传递性: Q 1 ≤ m p Q 2 Q_1 \le^{p}_{m} Q_2 Q 1 ≤ m p Q 2 Q 2 ≤ m p Q 3 Q_2 \le^{p}_{m} Q_3 Q 2 ≤ m p Q 3 Q 1 ≤ m p Q 3 Q_1 \le^{p}_{m} Q_3 Q 1 ≤ m p Q 3
N P − h a r d \mathcal{NP}-hard N P − h a r d
对于所有属于 N P \mathcal{NP} N P Q ′ Q' Q ′ Q Q Q Q ′ ≤ m p Q Q' \le^{p}_{m} Q Q ′ ≤ m p Q Q Q Q N P \mathcal{NP} N P Q Q Q N P − h a r d \mathcal{NP}-hard N P − h a r d
N P − 完 全 c o m p l e t e \mathcal{NP}-完全\;complete N P − 完 全 c o m p l e t e
如果问题 Q Q Q N P \mathcal{NP} N P Q ′ ≤ m p Q Q' \le^{p}_{m} Q Q ′ ≤ m p Q Q Q Q N P \mathcal{NP} N P Q Q Q N P − 完 全 \mathcal{NP}-完全 N P − 完 全
问题 Q Q Q N P \mathcal{NP} N P
所 有 N P 问 题 ≤ m p Q 所有\mathcal{NP}问题 \le^{p}_{m} Q 所 有 N P 问 题 ≤ m p Q Q Q Q N P − h a r d \mathcal{NP}-hard N P − h a r d
如果任意一个 N P − h a r d \mathcal{NP}-hard N P − h a r d P \mathcal{P} P P = N P \mathcal{P} = \mathcal{NP} P = N P
如果 P ≠ N P \mathcal{P} \ne \mathcal{NP} P = N P N P − h a r d \mathcal{NP}-hard N P − h a r d
如果 Q 1 ≤ m p Q 2 Q_1 \le^{p}_{m} Q_2 Q 1 ≤ m p Q 2 Q 1 Q_1 Q 1 N P − h a r d \mathcal{NP}-hard N P − h a r d Q 2 Q_2 Q 2 N P − h a r d \mathcal{NP}-hard N P − h a r d
例,给出一个“天然的” N P − 完 全 \mathcal{NP}-完全 N P − 完 全
Cook Theorem.
SAT (可满足) 问题是 N P − 完 全 \mathcal{NP}-完全 N P − 完 全
证明思路:
证明问题 Q Q Q N P − h a r d \mathcal{NP}-hard N P − h a r d
找到一个已知的 N P − 完 全 \mathcal{NP}-完全 N P − 完 全 Q 1 Q_1 Q 1
证明 Q 1 ≤ m p Q Q_1 \le^{p}_{m} Q Q 1 ≤ m p Q
证明问题 Q Q Q N P \mathcal{NP} N P
可满足问题 (SAT)、独立集问题 (Independent Set)、顶点覆盖问题 (Vertex-Cover)、子集求和问题 (Subset Sum)、分区问题 (Partition) 都是 N P − 完 全 \mathcal{NP}-完全 N P − 完 全
S P A C E ( s ( n ) ) SPACE(s(n)) S P A C E ( s ( n ) ) 是指计算机科学领域完成一个算法所需要占用的存储空间,一般是输入参数的函数。它是算法优劣的重要度量指标,一般来说,空间复杂度越小,算法越好。我们假设有一个图灵机来解决某一类语言的某一问题,设有 x x x
D S P A C E DS_{PACE} D S P A C E 类比于时间复杂度,如果存在一台【确定性图灵机】能够在输入为 x x x O ( s ( n ) ) O(s(n)) O ( s ( n ) ) Q Q Q D S P A C E ( s ( n ) ) DS_{PACE}(s(n)) D S P A C E ( s ( n ) )
对于一个【确定性】的图灵机,我们可以给出其常见的几种 【(确定的)空间复杂度 D S P A C E DS_{PACE} D S P A C E
1 S P A C E \mathsf{1SPACE} 1 S P A C E
1 S P A C E ≜ D S P A C E ( 1 ) \mathsf{1SPACE} \triangleq DS_{PACE}(1)
1 S P A C E ≜ D S P A C E ( 1 )
L S P A C E \mathsf{LSPACE} L S P A C E
L S P A C E ≜ D S P A C E ( log ( n ) ) \mathsf{LSPACE} \triangleq DS_{PACE}(\log(n))
L S P A C E ≜ D S P A C E ( log ( n ) )
P S P A C E \mathsf{PSPACE} P S P A C E
P S P A C E ≜ ⋃ k ∈ N D S P A C E ( n k ) \mathsf{PSPACE} \triangleq \bigcup_{k \in \mathbb{N}} DS_{PACE}(n^k)
P S P A C E ≜ k ∈ N ⋃ D S P A C E ( n k )
E X P S P A C E \mathsf{EXPSPACE} E X P S P A C E
E X P S P A C E ≜ ⋃ k ∈ N D S P A C E ( 2 n k ) \mathsf{EXPSPACE} \triangleq \bigcup_{k \in \mathbb{N}} DS_{PACE}(2^{n^k})
E X P S P A C E ≜ k ∈ N ⋃ D S P A C E ( 2 n k )
N S P A C E NS_{PACE} N S P A C E 相同的,如果存在一台【非确定性图灵机】能够在输入为 x x x O ( s ( n ) ) O(s(n)) O ( s ( n ) ) Q Q Q N S P A C E ( s ( n ) ) NS_{PACE}(s(n)) N S P A C E ( s ( n ) )
N S P A C E ( s ( n ) ) ⊆ D S P A C E ( s ( n ) 2 ) NS_{PACE}(s(n)) \subseteq DS_{PACE}(s(n)^2)
N S P A C E ( s ( n ) ) ⊆ D S P A C E ( s ( n ) 2 )
N L S P A C E \mathsf{NLSPACE} N L S P A C E s t − 联 通 度 CONN st-联通度 \text{ CONN} s t − 联 通 度 CONN N L S P A C E − complete \mathsf{NLSPACE}-\text{complete} N L S P A C E − complete
N L S P A C E ≜ N S P A C E ( log ( n ) ) \mathsf{NLSPACE} \triangleq NS_{PACE}(\log(n))
N L S P A C E ≜ N S P A C E ( log ( n ) )
N P S P A C E \mathsf{NPSPACE} N P S P A C E
N P S P A C E ≜ ⋃ k ∈ N N S P A C E ( n k ) = P S P A C E \mathsf{NPSPACE} \triangleq \bigcup_{k \in \mathbb{N}} NS_{PACE}(n^k) = \mathsf{PSPACE}
N P S P A C E ≜ k ∈ N ⋃ N S P A C E ( n k ) = P S P A C E
N E X P S P A C E \mathsf{NEXPSPACE} N E X P S P A C E
N E X P S P A C E ≜ ⋃ k ∈ N N S P A C E ( 2 n k ) = E X P S P A C E \mathsf{NEXPSPACE} \triangleq \bigcup_{k \in \mathbb{N}} NS_{PACE}(2^{n^k}) = \mathsf{EXPSPACE}
N E X P S P A C E ≜ k ∈ N ⋃ N S P A C E ( 2 n k ) = E X P S P A C E