本文章是根据瑞典皇家理工学院课件总结归纳而成。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考资料:
- KTH Royal Institute of Technology : Lagrange Multipliers and the Karush-Kuhn-Tucker conditions
目的
我们想要找到一个满足一些约束的函数的最大值或最小值
公式描述
给定一个函数 f,不等式约束 g1,...,gm 和等式约束 h1,...,hl 都在在定义域 Ω⊂Rn 上的优化问题:
s.t.x∈Ωminf(x){∀igi(x)≤0∀jhj(x)=0
No constraints
Assume: Let f : Ω→R be a continuously differentiable function. 在定义域上连续可微
【局部最小值】的【充要条件】(Necessary and sufficient conditions):
x∗ is a local minimum of f(x) 当且仅当
-
f 在 x∗ 处是零梯度 (zero gradient):
∇xf(x∗)=0
-
f 的 Hessian 矩阵在 x∗ 处是半正定的 (positive semi-definite):保证f 在 x∗ 处是“波谷”
vt(∇2f(x∗))v≥0,∀v∈Rn∇xx2f(x)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦⎥⎥⎥⎥⎥⎤←HessianMatrix
【局部最大值】的【充要条件】(Necessary and sufficient conditions): x∗ is a local minimum of f(x) 当且仅当
-
f 在 x∗ 处是零梯度 (zero gradient):
∇xf(x∗)=0
-
f 的 Hessian 矩阵在 x∗ 处是半正定的 (positive semi-definite):保证f 在 x∗ 处是“波谷”
vt(∇2f(x∗))v≤0,∀v∈Rn∇2f(x)=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱⋯∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦⎥⎥⎥⎥⎥⎤←HessianMatrix
Equality Constrainsts
问题提出:
s.t.x∈R2minf(x)hi(x)=0,∀i∈{1,2,...,l}
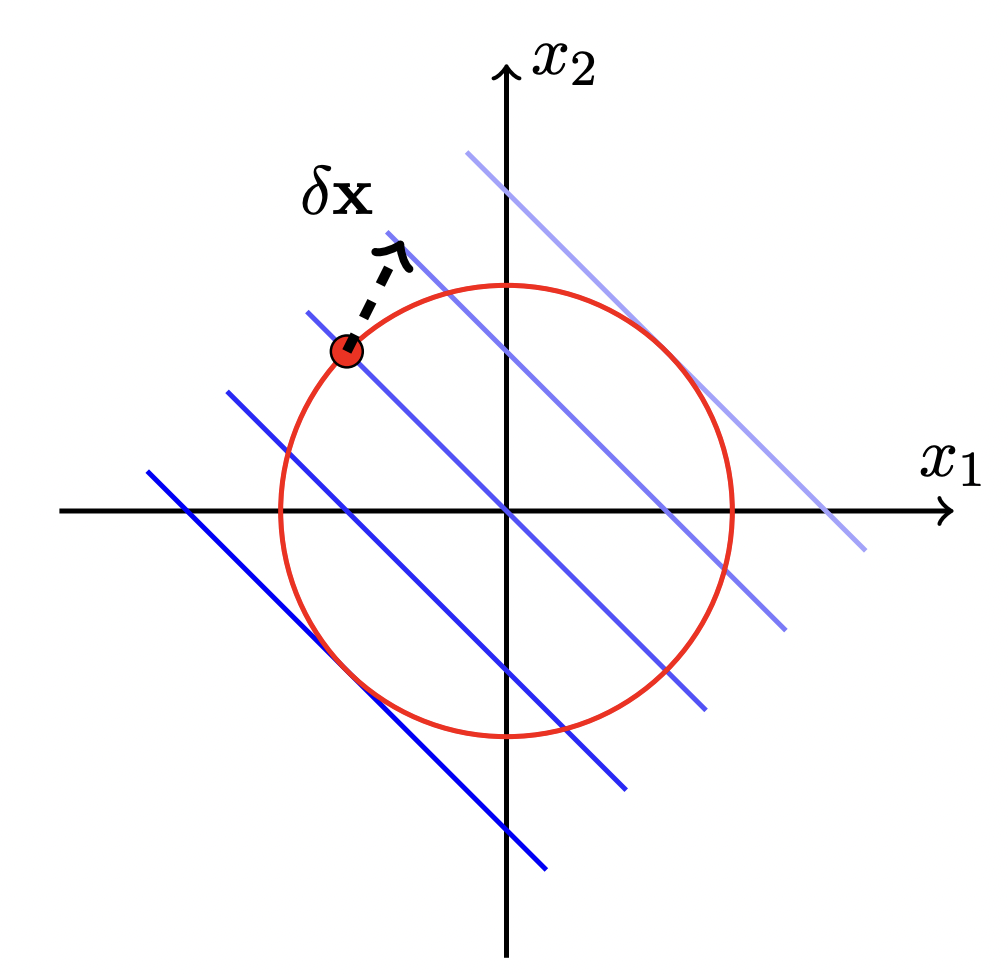
举例:
s.t.f(x)=x1+x2h(x)=x12+x22−2
-
可行点 (feasible point) xF∈ 可行域 (feasible region) 满足约束 h(x)=x12+x22−2=0,图形上的表示就是在 x12+x22−2 的圆上
-
目标函数 f(x)=x1+x2 的梯度方向 ∇xf(x)=[1,1]T,所以它的负梯度方向为 −∇xf(x)=[−1,−1]T
-
我们找到一个点 xi 满足约束:其中 α 为步长,δxi 为 xi 点的运动方向
- h(xF+αδxi)=0(确保在圆上)
- f(xF+αδx)<f(xF)(确保移动后的函数值 < 移动前)
-
一个点 xi 要沿着 f(x) 的最速下降 (the steepest descent) 方向,即负梯度方向为 −∇xf(x)=[−1,−1]T ;但是 xi 还要满足等式约束,所以我们要确保 δxi 与 负梯度方向 −∇xf(x) 的夹角为锐角,即内积 δxi⋅(−∇xf(xF))>0
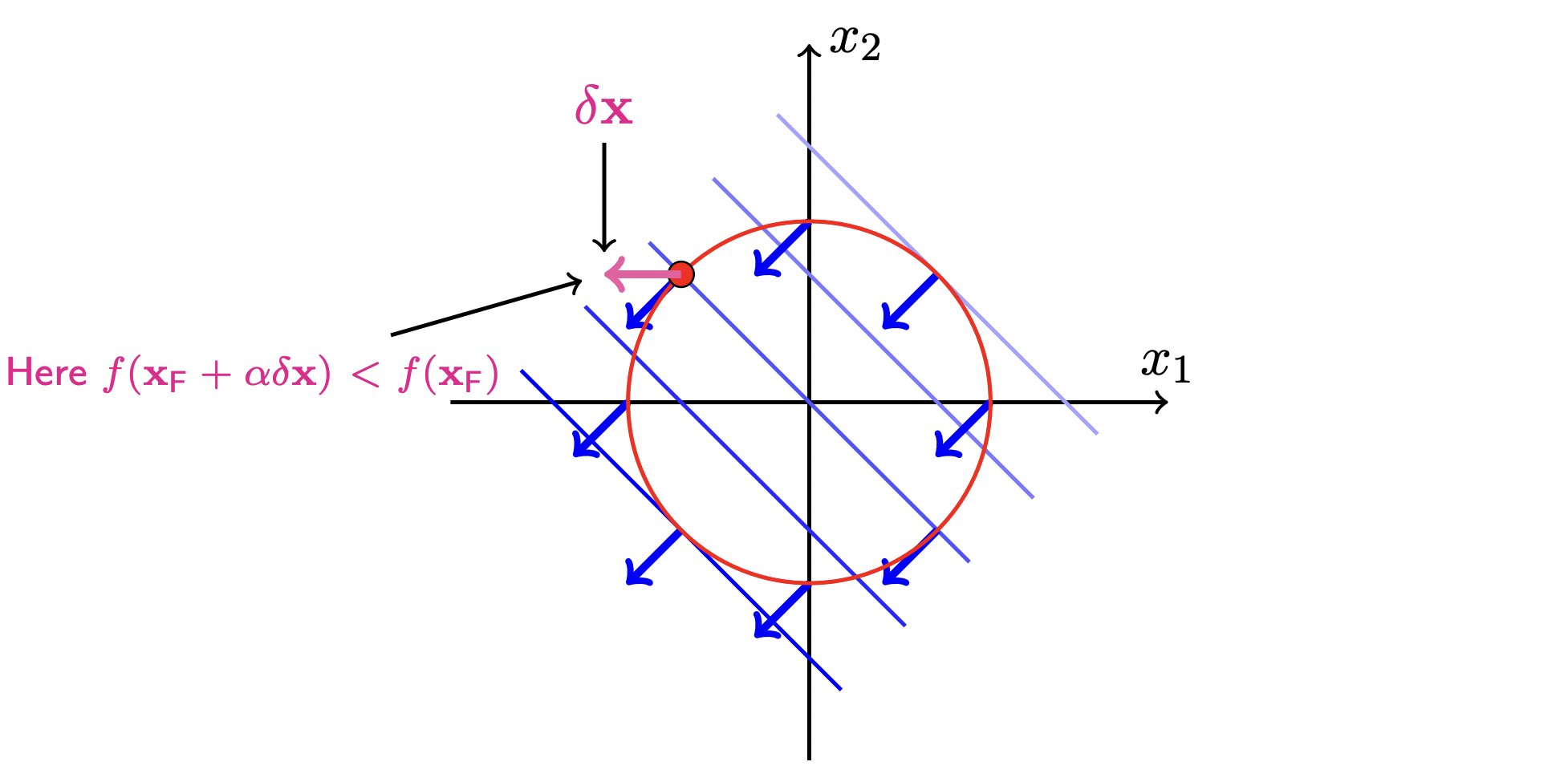
- 至此,我们就找到了满足约的点 xi 移动的方向,即与目标函数 f(x) 负梯度方向的夹角为锐角的约束函数 h(x) 的切线方向。那么,什么时候停止移动呢?
-
从图像中我们可以看到,当目标函数 f(x) 与约束函数 h(x) 相切的时候,我们可以取到局部极值点 (临界点 critical point),即 目标函数 f(x) 的梯度方向与约束函数 h(x) 的梯度方向共线:
∇xf(xF)=μ∇xh(xF)⇒∇xf(xF)+μ∇xh(xF)=0①
这个条件【确保局部极值】
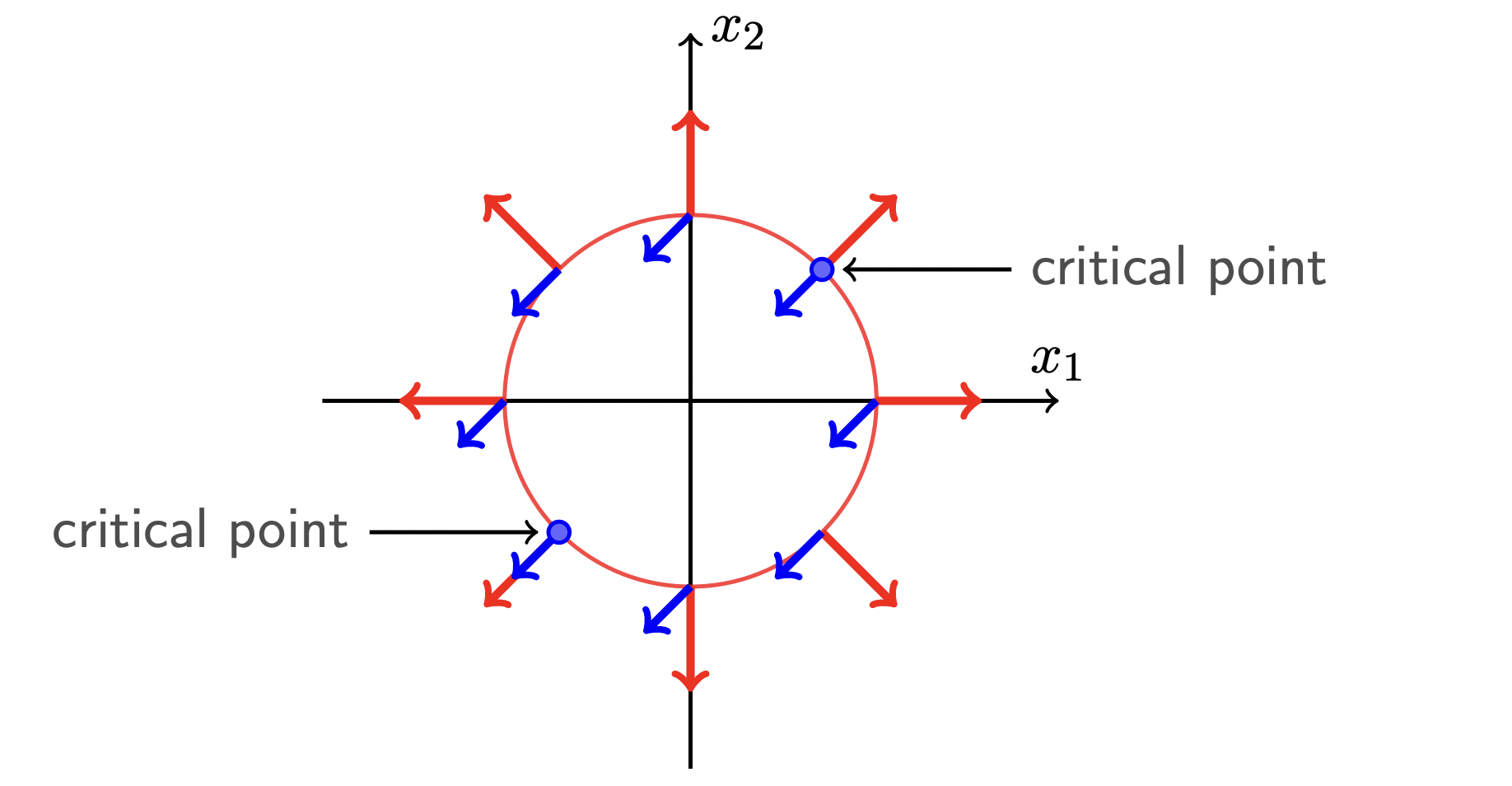
而此时, xi 移动的方向 δxi 始终与约束函数 g(x) 梯度方向 ∇xh(x) 正交,即
δxi⋅μ∇xh(xF)=δxi⋅(−∇xh(xF))
我们重新构造这个优化问题 (P),并推广到多等式约束:
s.t.x∈R2minf(x)hi(x)=0,∀i∈{1,2,...,l}
我们定义拉格朗日函数 L:
L(x,μ)=f(x)+i=1∑lμihi(x)
当 x∗ 是局部最小值时,存在唯一的 μ∗ 满足约束:
- ∇xL(x∗,μ∗)=0⇐∇xf(xF)+μ∇xh(xF)=0①
- ∇μL(x∗,μ∗)=0⇐∂μi∂L(x,μi)=hi(x)=0满足约束条件
- ∇xx2L(x∗,μ∗)⪰0⇐Hessain matrix 半正定:满足局部极小
Inequality Constraints
问题提出:
s.t.x∈R2minf(x)gj(x)≤0,∀j∈{1,2,...,m}
Case 1 : 可退化到无约束
举例:
s.t.f(x)=x12+x22h(x)=x12+x22−1
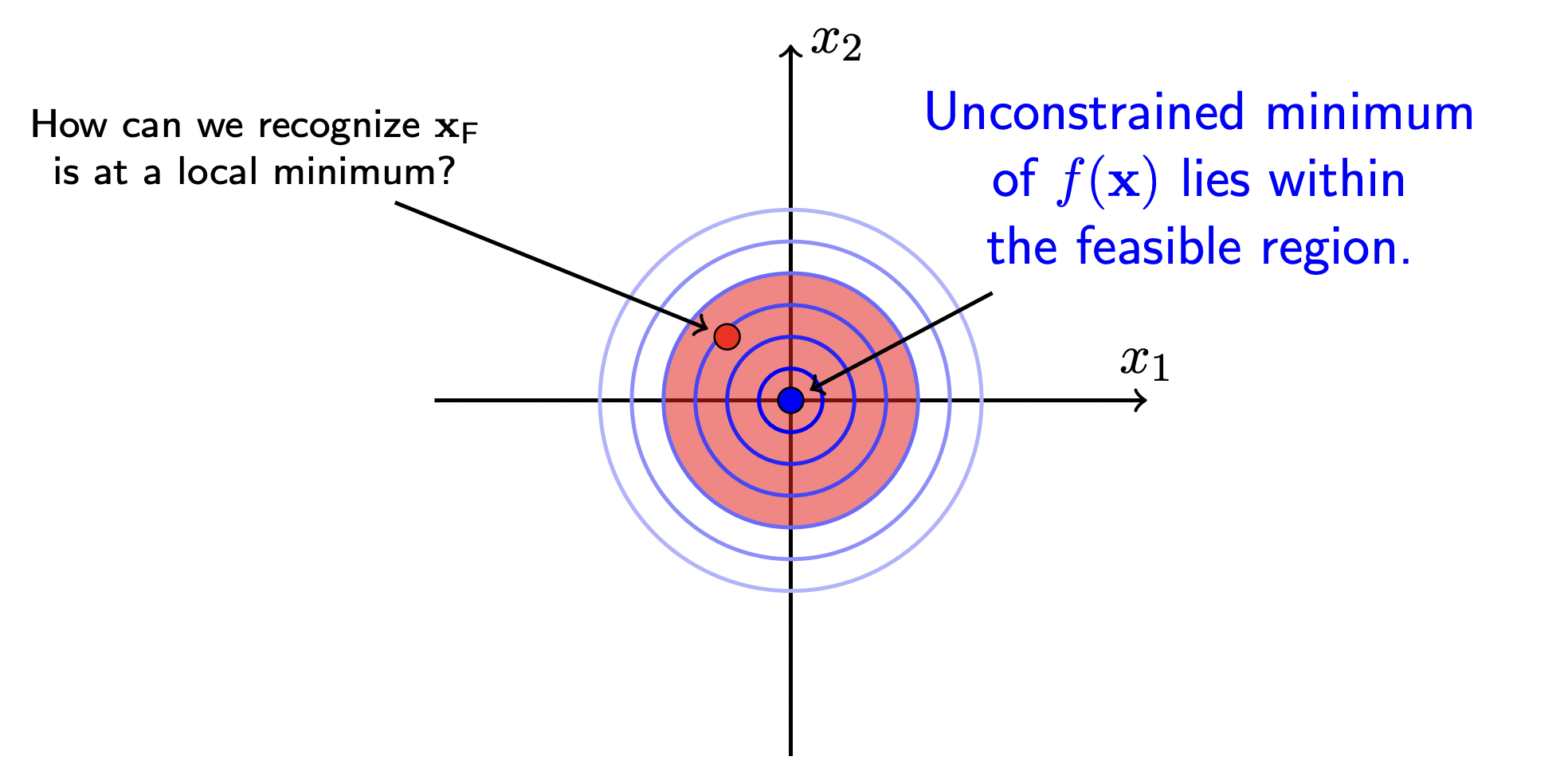
- 可以从图像中看出,当 f(x) 不加约束条件时的最优点为 (0,0)
- 可行点 (feasible point) xF∈ 可行域 (feasible region) 满足约束 h(x)=x12+x22−1=0,图形上的表示就是在 x12+x22−1 的圆上
- 当 f(x) 加入约束条件时的最优点还是 (0,0)
- 说明有无约束条件对这个问题的求解并没有影响
- 此时我们就可以将这个约束优化问题退化成无约束问题:
- f(x) 在 x∗ 处是零梯度 (zero gradient):∇xf(x∗)=0
- f 的 Hessian 矩阵在 x∗ 处是半正定的 (positive definite) :∇xx2f(x∗)⪰0
Case 2 : 不等式约束
我们更改上一例题的条件:
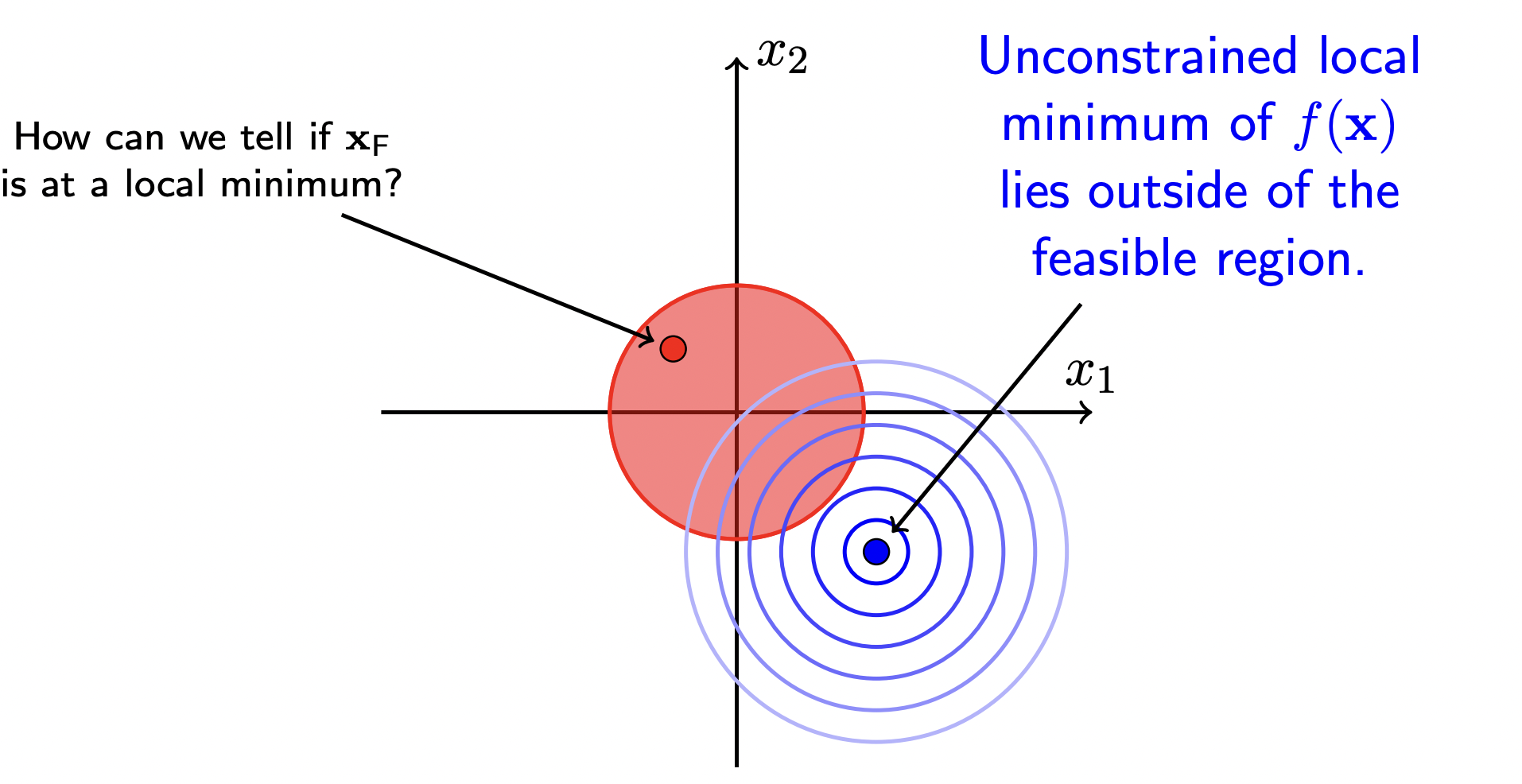
s.t.f(x)=(x1−1.1)2+(x2−1.1)2h(x)=x12+x22−1
-
可以从图像中看出,当 f(x) 不加约束条件时的最优点为 (1.1,−1.1)
-
可行点 (feasible point) xF∈ 可行域 (feasible region) 满足约束 h(x)=x12+x22−1=0,图形上的表示就是在 x12+x22−1 的圆上
-
当 f(x) 加入约束条件时的最优点并不在原来的 (1.1,−1.1) 点
-
在这种情况下,极值在约束面上,即 g(x∗)=0,此时就与等式约束条件一致了
-
所以参考等式约束问题,最优值出现在目标函数 f(x) 的梯度方向与约束函数 h(x) 的梯度方向共线:
−∇xf(x)=λ∇xg(x),λ>0⇒∇xf(x)+λ∇xg(x)=0②
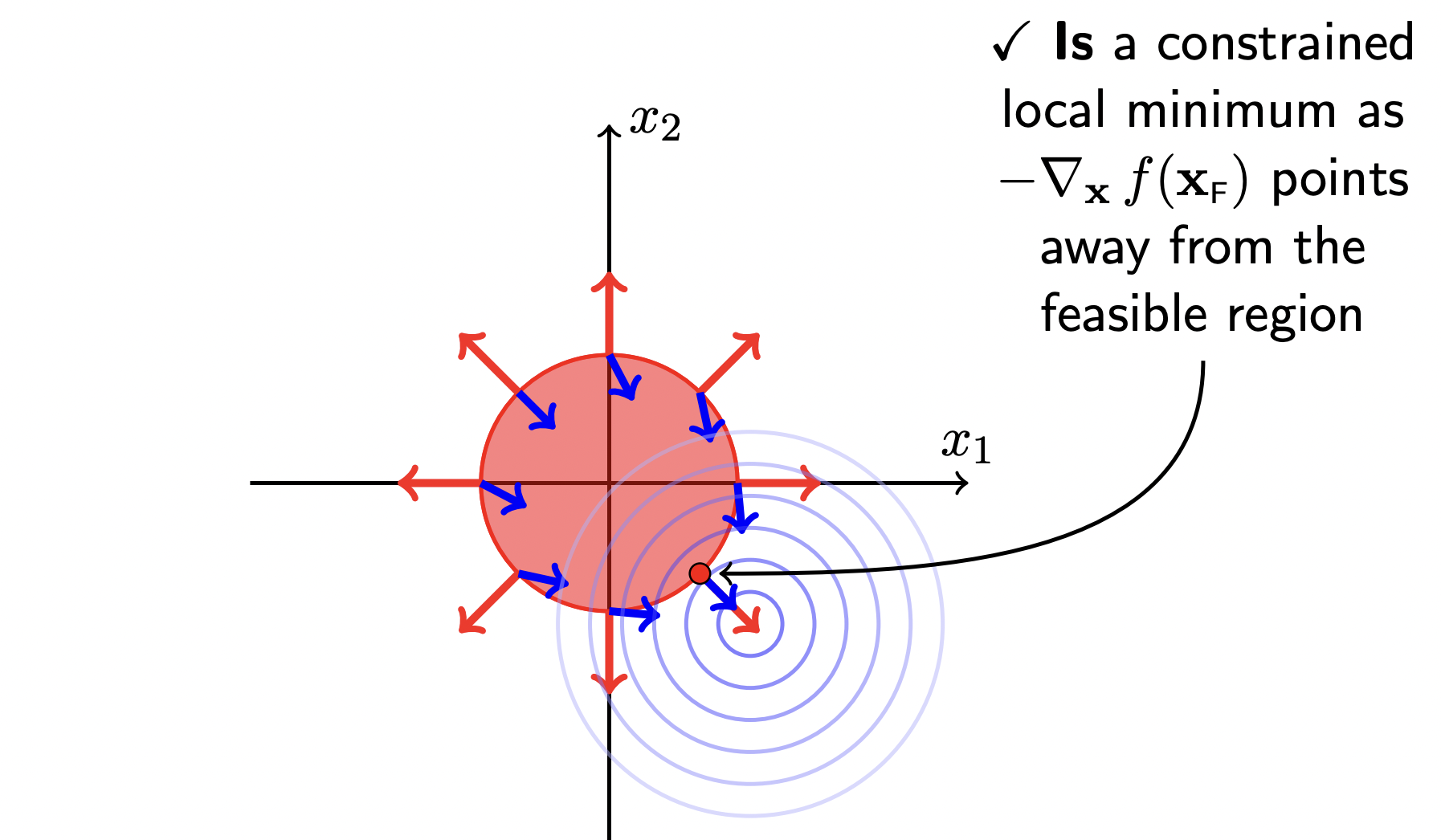
总结两种情况
s.t.x∈R2minf(x)gj(x)≤0,∀j∈{1,2,...,m}
Case 1 : 无约束时的局部极小值在可行域【中】
- g(x∗)<0⇐在可行域里
- ∇xf(x∗)=∇xf(x∗)+λ(=0)∇xg(x∗)=0⇐KKT条件1
- ∇xx2f(x∗)⪰0⇐Hessian矩阵是半正定的
Case 2 : 无约束时的局部极小值在可行域【外】
- g(x∗)=0⇐KKT条件3
- −∇xf(x∗)+λ∇xg(x∗)=0,λ>0⇐KKT条件1
- ∇xx2f(x∗)⪰0⇐Hessian矩阵是半正定的
KKT 条件4 :x∗ 是可行点
多等式和多不等式的 KKT 条件
给定一个函数 f,不等式约束 g1,...,gm 和等式约束 h1,...,hl 都在在定义域 Ω⊂Rn 上的优化问题:
s.t.(P):x∈Ωminf(x){hi(x)=0,∀i∈{1,2,...,l}gj(x)≤0,∀j∈{1,2,...,m}
我们定义拉格朗日函数 L:
L(x,λ,μ)=f(x)+i=1∑lμihi(x)+j=1∑mλjgj(x))
当 x∗ 是局部最小值时,存在唯一的 μ∗ 满足约束:
-
∇xL(x∗,μ∗,λ∗)=0⇐∇xf(x∗)+∑i=1lμi∇xhi(x∗)+∑j=1mλj∇xgj(x∗)=0
-
λj∗≥0 for j=1,...,m
-
λj∗gj(x∗)=0 for j=1,...,m
-
gj(x∗)≤0 for j=1,...,m
-
gi(x∗)=0 for i=1,...,l
-
∇xx2L(x∗,λ∗)≻0⇐Hessain matrix 正定:满足局部极小





