运筹学

前言

本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第七学期课程*“Recherche Operation”* 总结而来的【部分课程笔记】。碍于本人学识有限，部分叙述难免存在纰漏，请读者注意甄别。

总而言之，运筹学就是从真实系统中建立模型，用数学的形式表示出来。

附录一：$\mathcal{KKT}$ 和 拉格朗日乘子

关系：$\mathcal{KKT}$ ，拉格朗日乘子 和 线性规划

本科阶段，我们在高等数学中认识了拉格朗日乘子。其研究范围可以认为是

$拉格朗日乘子 \sim 在约束条件为强约束（即约束条件都为等式）的情况下，非线性规划的问题中求解最优值。$

而 $\mathcal{KKT}$ 研究范围可以认为是

$\mathcal{KKT} \sim 在约束条件为弱约束（即约束条件有不等式）的情况下，非线性规划的问题中求解最优值。$

线性规划问题的研究范围可以认为是

$LP(线性规划) \sim 在约束条件下，线性规划的问题中求解最优值。$

所以我们可以认为 $\mathcal{KKT} > 拉格朗日乘子$，$\mathcal{KKT} > LP > 整数线性规划$

拉格朗日乘子

引例：我们有如下问题

$W = f(x,y,z) = 3x^2 + 2y^2 - 4z^2\\ s.t.\left\{\begin{aligned} 3x + 4y -z = 0\\ 6x^2 + y - z^2 = 0 \end{aligned}\right.$

由于对于拉格朗日乘子法的证明过程并不感兴趣，所以在此不加证明地直接给出其计算方法：

1. 已知我们想要求解目标函数 $W = f(x,y,z) = 3x^2 + 2y^2 - 4z^2$ 的最大值$maxW$ 或最小值$minW$​，我们有两个约束条件$g_1,g_2$： $s.t.\left\{\begin{aligned} g_1:3x + 4y -z = 0\\ g_2:6x^2 + y - z^2 = 0 \end{aligned}\right.$

2. 我们引入拉格朗日乘子 $\lambda _i$ 辅助求解该问题。拉格朗日乘子 $\lambda _i$ 引入的数量由约束条件的数量决定。所以本引例中需要引入两个拉格朗日乘子 $\lambda_1, \lambda_2$ 。

3. 构造一个包含拉格朗日乘子 $\lambda_1,\lambda_2$ 的新函数 $F(x,y,z,\lambda_i) = f(x,y,z) + \lambda_1g_1 + \lambda_2g_2 + ...+ \lambda_ng_n$ 。所以原函数可转化为以下的拉格朗日函数：

   $\begin{aligned} F(x,y,z,\lambda_1,\lambda_2) & = f(x,y,z) + \lambda_1g_1 + \lambda_2g_2\\ &= 3x^2 + 2y^2 - 4z^2 + \lambda_1 (3x + 4y -z) + \lambda_2(6x^2 + y - z^2) \end{aligned}$

4. 则我们就可以通过导数的方法求解此问题 $F(x,y,z,\lambda_1,\lambda_2)$ 。对 $F$ 求偏导，有几个自变量，就求几次偏导，令其都等于 0。方程 ①②③④⑤ 一定能得到不止一组的解 $(x_i,\; y_i,\; z_i,\; {\lambda_1}_i,\; {\lambda_2}_i)$ ，将解得的解 $(x_i,\; y_i,\; z_i,\; {\lambda_1}_i,\; {\lambda_2}_i)$ 代入原来的目标函数 $W=f(x,y,z)$ 中，算出的 $W_{max}$ 和 $W_{min}$。

   $\left\{\begin{aligned} \frac {\partial F}{\partial x} =0 \qquad ①\\ \frac {\partial F}{\partial y} =0 \qquad ②\\ \frac {\partial F}{\partial z} =0 \qquad ③\\ \frac {\partial F}{\partial {\lambda_1}} =0 \qquad ④\\ \frac {\partial F}{\partial {\lambda_2}} =0 \qquad ⑤\\ \end{aligned}\right. \quad \stackrel{解}{\Longrightarrow} \quad \begin{pmatrix} x_i\\ y_i\\ z_i\\ {\lambda_1}_i\\ {\lambda_2}_i\\ \end{pmatrix} \quad \stackrel{代入原来的目标函数}{\Longrightarrow} \quad f(x_i,y_i,z_i) \quad \stackrel{找Min和Max}{\Longrightarrow} \quad (W_{max}, W_{min})$

$\mathcal{KKT}$

$\mathcal{KKT}$ 本质上是拉格朗日乘数法的推广，即推广到弱约束（即约束条件有不等式）条件。

【拉格朗日乘数法】：

$Z_{max}或Z_{min} = f(x,y,z,...)\\ g_1 =0, \; g_2 =0,\; g_3 = 0\\ ①观察约束条件，有几个约束，方程就引入几个拉格朗日乘子 \lambda ,对于\lambda 无限制\\ ②构建F(x,y,z,\lambda_1, \lambda_2, \lambda_3) = f(x,y,z) + \lambda_1g_1 + \lambda_2g_2 + \lambda_3g_3\\ ③\left\{\begin{aligned} \frac {\partial F}{\partial x} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \frac {\partial F}{\partial y} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \frac {\partial F}{\partial z} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \frac {\partial F}{\partial {\lambda_1}} =0 \quad {\Longrightarrow} \quad g_1= 0 \\ \frac {\partial F}{\partial {\lambda_2}} =0 \quad {\Longrightarrow} \quad g_2= 0 \\ \frac {\partial F}{\partial {\lambda_3}} =0 \quad {\Longrightarrow} \quad g_3= 0 \\ \end{aligned}\right. \quad {\Longrightarrow} \quad 约束 g_i=0\\ \\ ④ 解方程组 \\ ⑤ 将所有解代入目标函数 f(x,y,z)，判断最大值和最小值\\ ⑥ 结束\\$

【KKT】：

$Z_{max}或Z_{min} = f(x,y,z,...)\\ g_1 \le 0, \; g_2 \ge 0, \; g_n = 0\\ ⓪化为标准型^*\\ ①观察约束条件，有几个约束，方程就引入几个拉格朗日乘子 \lambda^* ,\lambda^* \ge 0\\ \begin{aligned} ②构建\mathcal{L}(x,y,z,\lambda_1^*, \lambda_2^*, \lambda_3^*, \lambda_4^*) & = f(x,y,z) + \lambda_1^*g'_1 + \lambda_2^*g'_2 + \lambda_3^*g'_3 + \lambda_4^*g'_4\\ & = f(x,y,z) + \lambda_1^*g_1 - \lambda_2^*g_2 + \lambda_3^*g_3 - \lambda_4^*g_3 \end{aligned}\\ ③\left\{\begin{aligned} \frac {\partial \mathcal{L}}{\partial x} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \frac {\partial \mathcal{L}}{\partial y} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \frac {\partial \mathcal{L}}{\partial z} =0 \quad \stackrel{本质是}{\Longrightarrow} \quad F对目标函数的自变量求偏导\\ \lambda_1^*g_1 = 0 \\ \lambda_2^*(-g_2) = 0 \\ \lambda_3^*(g_3) = 0 \\ \lambda_4^*(-g_3) = 0 \end{aligned}\right. \quad {\Longrightarrow} \quad 广义乘子 \lambda_i^*\times 约束g_i = 0 \\ \\ ④ 解方程组 \\ ⑤ 将所有解代入目标函数 f(x,y,z)，判断最大值和最小值\\ ⑥ 结束\\$

0. 化为【标准型】：

   对于上述例子，我们可以看到【约束条件】很“混乱”，即符号不同，有$\le, \ge ,=$ ，我们需要将它们化为统一标准形式（“$代数式 \ge 0$”）。

   • 对于 $=$ ：$g_3 = 0 \Leftrightarrow g_3\le 0 且 g_3 \ge 0$
   • 对于 $\le$ ：$g_1 \le 0 \Leftrightarrow -g_1 \ge 0$

   所以我们可以按上述规则将约束条件改写为

   $s.t.\left\{\begin{aligned} - g_1 \ge 0\\ g_2 \ge 0\\ g_3 \ge 0\\ -g_3 \ge 0\\ \end{aligned}\right. \quad \stackrel{看作整体}{\Longrightarrow} \quad s.t.\left\{\begin{aligned} g_1' = - g_1 \ge 0\\ g_2' = g_2 \ge 0\\ g_3' = g_3 \ge 0\\ g_4' = -g_3 \ge 0\\ \end{aligned}\right.$

   不过更建议化成 “$代数式 \le 0$” 的形式，因为可以更好的和拉格朗日乘数法结合观察：

   $s.t.\left\{\begin{aligned} - g_1 \ge 0\\ g_2 \ge 0\\ g_3 \ge 0\\ -g_3 \ge 0\\ \end{aligned}\right. \quad \stackrel{看作整体}{\Longrightarrow} \quad s.t.\left\{\begin{aligned} g_1' = g_1 \le 0\\ g_2' = -g_2 \le 0\\ g_3' = g_3 \le 0\\ g_4' = -g_3 \le 0\\ \end{aligned}\right.$

1. 观察约束条件，有几个约束，方程就引入几个广义拉格朗日乘子 $\lambda^*$：$\lambda_1^*, \lambda_2^*, \lambda_3^*, \lambda_4^*$ 。注意，在拉格朗日乘数法中，引入拉格朗日乘子 $\lambda$ 后并无任何限制，但是在 $KKT$ 中，我们要求所有的广义拉格朗日乘子

   $\lambda^* \ge 0$

2. 构造一个包含广义拉格朗日乘子 $\lambda_1^*, \lambda_2^*, \lambda_3^*, \lambda_4^*$ 的新函数 $\mathcal{L} (x,y,z,\lambda_i^*) = f(x,y,z) + \lambda_1^*g_1 + \lambda_2^*g_2 + ...+ \lambda_n^*g_n$ 。所以原函数可转化为以下的广义拉格朗日函数：

   $\begin{aligned} \mathcal{L} (x,y,z,\lambda_1^*, \lambda_2^*, \lambda_3^*, \lambda_4^*) & = f(x,y,z) + \lambda_1^*g'_1 + \lambda_2^*g'_2 + \lambda_3^*g'_3 + \lambda_4^*g'_4\\ & = f(x,y,z) + \lambda_1^*g_1 - \lambda_2^*g_2 + \lambda_3^*g_3 - \lambda_4^*g_3 \end{aligned}\\$

3. 则我们就可以通过导数的方法求解此问题 $\mathcal{L} (x,y,z,\lambda_1^*, \lambda_2^*, \lambda_3^*, \lambda_4^*)$ 。写出如下形式的方程。方程定能得到不止一组的解 $(x_i,\; y_i,\; z_i,\; {\lambda_1^*}_i, {\lambda_2^*}_i, {\lambda_3^*}_i, {\lambda_4^*}_i$ ，将解得的解 $(x_i,\; y_i,\; z_i,\; {\lambda_1^*}_i, {\lambda_2^*}_i, {\lambda_3^*}_i, {\lambda_4^*}_i$ 代入原来的目标函数 $Z=f(x,y,z)$ 中，算出的 $Z_{max}$ 和 $Z_{min}$。

   $\left\{\begin{aligned} \frac {\partial \mathcal{L}}{\partial x} =0 \\ \frac {\partial \mathcal{L}}{\partial y} =0 \\ \frac {\partial \mathcal{L}}{\partial z} =0 \\ \lambda_1^*g_1 = 0 \\ \lambda_2^*(-g_2) = 0 \\ \lambda_3^*(g_3) = 0 \\ \lambda_4^*(-g_3) = 0 \end{aligned}\right. \quad \stackrel{解}{\Longrightarrow} \quad \begin{pmatrix} x_i\\ y_i\\ z_i\\ {\lambda_1^*}_i\\ {\lambda_2^*}_i\\ {\lambda_3^*}_i\\ {\lambda_4^*}_i\\ \end{pmatrix} \quad \stackrel{代入原来的目标函数}{\Longrightarrow} \quad f(x_i,y_i,z_i) \quad \stackrel{找Min和Max}{\Longrightarrow} \quad (Z_{max}, Z_{min})$

例题

$f(x) = (x-3)^2，0 \le x \le 5，求_{min}f(x)$

0. 规范化（化标准型“$代数式 \le 0$”）：

   $0 \le x \le 5 \quad \Rightarrow \quad \begin{aligned} x \ge 0\\ x \le 5 \end{aligned} \quad \Rightarrow \quad \begin{aligned} -x \le 0\\ x-5 \le 0 \end{aligned} \quad \Rightarrow \quad \begin{aligned} g_1 = -x \le 0\\ g_2 = x-5 \le 0 \end{aligned}$

1. 观察约束，有 2 个约束，所以引入 2 个广义拉格朗日乘子 $\lambda_1^*, \lambda_2^*$，

   $\lambda_1^* \ge 0 \\ \lambda_2^* \ge 0 \\$

2. 构建广义拉格朗日函数 $\mathcal{L} (x,\lambda_1^*, \lambda_2^*)$ :

   $\begin{aligned} \mathcal{L} (x,\lambda_1^*, \lambda_2^*) &= f(x) + \lambda_1^*g_1 + \lambda_2^*g_2 \\ &= (x-3)^2 + \lambda_1^*(-x) + \lambda_2^*(x-5) \end{aligned}$

3. 联立方程组：

   $\left\{\begin{aligned} \frac {\partial F}{\partial x} = 2(x-3) - \lambda_1^* + \lambda_2^* = 0 \qquad ①\\ \lambda_1^*g_1 = \lambda_1^* (-x) = 0 \qquad ② \\ \lambda_2^*g_2 = \lambda_2^* (x-5) = 0 \qquad ③ \\ \end{aligned}\right.$

4. 解方程组。(【注意⚠️】：一般需要详细讨论解的情况。)

   【1】我们先从 ② 式开始 ：$② \Rightarrow \lambda_1^* x = 0 \quad \stackrel{两种情况}{\Longrightarrow} \quad \lambda_1^*=0 \; 或\; x=0$

   1. 当 $\lambda_1^* \ne 0$ 时，我们可以得到 $x = 0$ 。我们再结合 $③\;\lambda_2^* (x-5) = 0$，我们得到 $\lambda_2^* = 0$ 。我们再结合 $ ① ; 2(x-3) - \lambda_1^* + \lambda_2^* = 0$ ，我们可以解得 $\lambda_1^* = -6 < 0$ 。因为我们有约束条件 $\lambda_1^* \ge 0$，所以我们要舍弃这组解。

   2. 当 $\lambda_1^* = 0$ 时，在 ② 式中 $x$ 可以是任意值，所以我们要结合 ① ③ 式：

      $\left\{\begin{aligned} 2(x-3) + \lambda_2^* = 0 \qquad ①\\ \lambda_2^* (x-5) = 0 \qquad ③ \\ \end{aligned}\right. \quad \stackrel{解得}{\Longrightarrow} \quad \left\{\begin{aligned} x = 3 \\ \lambda_2^* = 0\\ \end{aligned}\right. \quad 或 \quad \left\{\begin{aligned} x = 5 \\ \lambda_2^* = -4 < 0\\ \end{aligned}\right.$

      我们可以看出，其中存在一组解

      $\left\{\begin{aligned} x = 3 \\ \lambda_1^* = 0\\ \lambda_2^* = 0\\ \end{aligned}\right.$

   【2】我们再回到 ③ 式重新讨论：$ ③ ; \lambda_2^* (x-5) = 0 \quad \stackrel{两种情况}{\Longrightarrow} \quad \lambda_2^*=0 ; 或; x=5$

   1. $x=5, \lambda_2^* \ne 0$ 的情况已经在 ② 式的第 2 种情况中讨论过了，所以跳过。

   2. 当 $\lambda_2^* = 0$ 时，在 ③ 式中 $x$ 可以是任意值，所以我们要结合 ① ② 式：

      $\left\{\begin{aligned} 2(x-3) - \lambda_1^* = 0 \qquad ①\\ \lambda_1^* (-x) = 0 \qquad ② \\ \end{aligned}\right. \quad \stackrel{解得}{\Longrightarrow} \quad \left\{\begin{aligned} x = 0 \\ \lambda_1^* = -6 < 0\\ \end{aligned}\right. \quad 或 \quad \left\{\begin{aligned} x = 3 \\ \lambda_1^* = 0\\ \end{aligned}\right.$

      我们可以看出，其中存在一组解

      $\left\{\begin{aligned} x = 3 \\ \lambda_1^* = 0\\ \lambda_2^* = 0\\ \end{aligned}\right.$

5. 所以 $_{min}f(x) = f(3) = (3-3)^2 = 0$ 。

【一点想法】

当我们使用$\mathcal{KKT}$得到一个解时，若该解中某个广义拉格朗日乘子 $\lambda_i^* >0$，则说明 $\lambda_i$ 所对应的约束 $g_i = 0$，即这个解所对应的点恰好落在了曲线 $g_i = 0$ 上。

附录二：线性代数回顾

简言之，线性代数的目的就是求解线性方程组。经典的理论是与几何联系起来。

方法论

graph LR
提取系统信息 --经过运算--> 判断解的情况
提取系统信息 --经过运算--> 解方程

$\left\{\begin{aligned} a_{1,1}x_1 + a_{1,2}x_2 + ... a_{1,n}x_n = \; b_1 \\ a_{2,1}x_1 + a_{2,2}x_2 + ... a_{2,n}x_n = \; b_2 \\ ... \quad ... \quad ... \quad ... \quad \\ a_{i,1}x_1 + a_{i,2}x_2 + ... a_{i,n}x_n = \; b_i \\ ... \quad ... \quad ... \quad ... \quad \\ a_{n,1}x_1 + a_{n,2}x_2 + ... a_{n,n}x_n = \; b_n \\ \end{aligned}\right. \quad \stackrel{提取系统信息}{\Longrightarrow} \quad \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{n,1} & a_{n,2} & \cdots & a_{n,n}\\ \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{pmatrix} = \begin{pmatrix} b_1\\ b_2\\ \vdots\\ b_n\\ \end{pmatrix}$

【秩】Rank：矩阵的本质属性。如果把矩阵看成一个个行向量或者列向量，如果其中有一个向量能被另一个向量线性表示的话，那么该矩阵表示的方程组有无穷多解；如果没有任何一个向量能被另一个向量线性表示的话，那么该矩阵表示的方程组有唯一解。【秩】的本质就是矩阵中独立向量的个数。

【行列式】：行列式的本质是代表一种算法的运算符，和 $+,-,\times,\div$ 类似。用 $A_{2 \times 2}$ 举例：

$A_{2 \times 2} = \begin{vmatrix} x & y \\ z & v \end{vmatrix} = xv-yz$

【行列式的几何意义】

• 二阶：是这 2 个向量围成的平行四边形的面积
• 三阶：是这 3 个向量围成的平行六面体的体积
• n阶：n维超立方体的体积

所以，行列式一旦 $=0$ ，说明行列式对应的矩阵里有线性相关的向量。当行列式 $\ne 0$ 时，说明行列式对应的矩阵是满秩的。

第一部分：线性规划

1.1 线性规划问题及数学模型

1.1.1 问题的提出

我们可以考虑以下一个简单的例子：

例1，某工厂在计划期内要安排生产甲、乙两种产品，已知生产单位产品所需的设备合时及 A、B 两种原材料的消耗如表所示。该厂每生产一件产品甲可获利2元，一件产品乙可获利3元，问该工厂如何安排生产计划使利润最大？

	产品甲	产品乙	资源限量
设备	1 台时/件	2 台时/件	8 台时
原材料 A	4 kg/件	0	16 kg
原材料 B	0	4 kg/间	12 kg
利润	2 元	3 元

我们可以根据以上描述建立一个数学模型：

$Profit_{max} = 2x+3y\\ s.t.\left\{\begin{aligned} x_1 + 2x_2 \le 8 \\ 4x_1 \le 16 \\ 4x_2 \le 12 \\ x_1, x_2 \ge 0 \end{aligned}\right.$

其中，

• $x_1$ 和 $x_2$ 为【决策变量】；
• $Profit_{max} = 2x+3y$ 是【决策函数】，是决策者希望达到的计划目标；
• $s.t.$ 为“subject to”，为【约束条件】，为决策变量取值时受到的限制。

这类优化问题的共同特征：

1. 每一个问题都用一组决策变量表示某一方案，这组决策变量的值就代表一个具体方案。一般取值非负且连续。
2. 要有建模的相关数据，如资源拥有量、消耗资源定额、创造的新价值量等并构造不矛盾的约束条件，由线性等式或不等式来表示。
3. 都有一个要达到的目标，可用决策变量及其有关的价值系数构成的线性函数来表示，一般要求最大或最小

线性规划问题模型的【一般表达式形式】为：

$max(min)Z = c_1x_1 + c_2x_2 + c_3x_3 + ...+ c_nx_n\\ s.t.\left\{\begin{aligned} a_{1,1}x_1 + a_{1,2}x_2 + ... a_{1,n}x_n \le (\ge ,=) \; b_1 \\ a_{2,1}x_1 + a_{2,2}x_2 + ... a_{2,n}x_n \le (\ge ,=) \; b_2 \\ ... \quad ... \quad ... \quad ... \quad \\ a_{i,1}x_1 + a_{i,2}x_2 + ... a_{i,n}x_n \le (\ge ,=) \; b_i \\ ... \quad ... \quad ... \quad ... \quad \\ a_{n,1}x_1 + a_{n,2}x_2 + ... a_{n,n}x_n \le (\ge ,=) \; b_n \\ x_1, x_2, ... x_n \ge 0 \end{aligned}\right.$

其中，

• $c_n$ 为价值系数
• $a_{ij}$ 为技术系数
• $b_i$ 为资源限制
• $x_1, x_2, ... x_n \ge 0$ 为决策变量约束

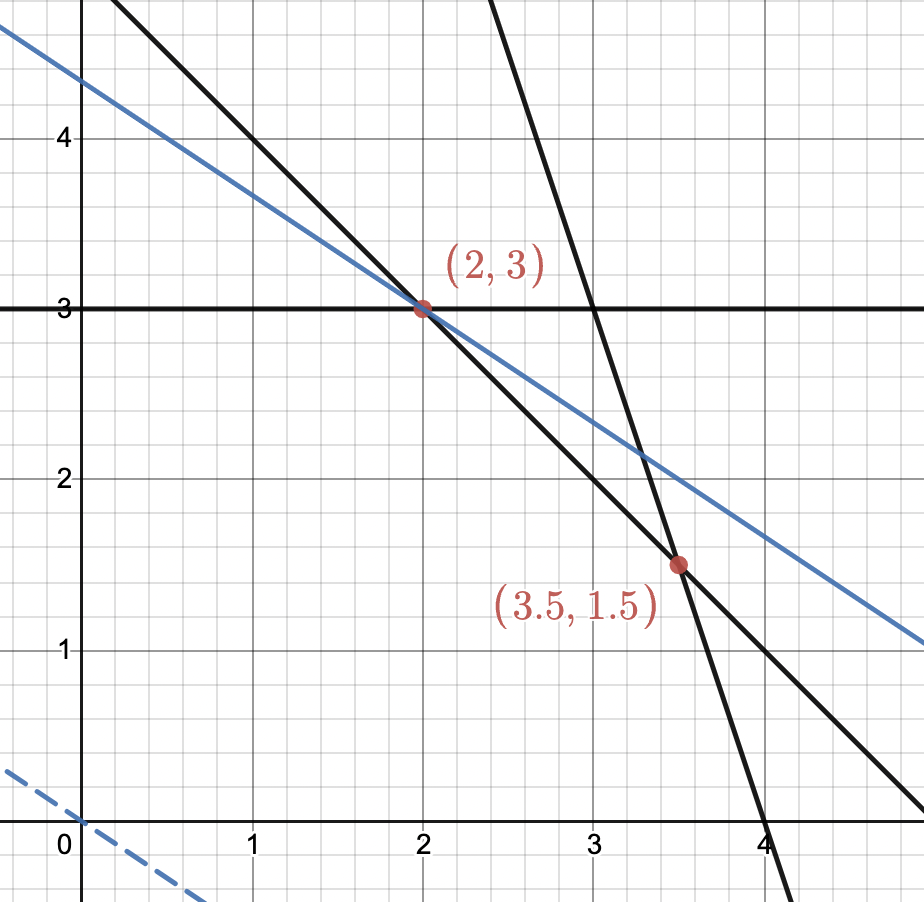
1.1.2 图解法

图解法求解步骤（只适用于两个决策变量的问题 - 二维）：

1. 由全部约束条件作图求出【可行域】；
2. 作目标函数【等值线】，确定使目标函数最优的移动方向；
3. 平移目标函数的等值线，找出【最优点】，算出最优值。

1.1.3 化标准型

参考以上线性规划问题模型的一般表达式形式，我们发现线性规划的共同特证：

1. 决策变量：每个问题都用一组决策变量表示某个方案

   决策变量：决策变量的取值一般都是非负且连续的

2. 约束条件：与决策变量不矛盾的条件，用线性等式或不等式表示

3. 目标函数：决策变量与价值系数组成，一般要求实现最大或最小

所以我们建模的一般思路为：确定决策变量，写出目标函数，找出约束条件。

如果我们想用单纯形法求解线性规划问题，第一步是将一般表达式为以下的标准型：

$maxZ = c_1x_1 + c_2x_2 + c_3x_3 + ...+ c_nx_n\\ s.t.\left\{\begin{aligned} a_{1,1}x_1 + a_{1,2}x_2 + ... a_{1,n}x_n = \; b_1 \\ a_{2,1}x_1 + a_{2,2}x_2 + ... a_{2,n}x_n = \; b_2 \\ ... \quad ... \quad ... \quad ... \quad \\ a_{i,1}x_1 + a_{i,2}x_2 + ... a_{i,n}x_n = \; b_i \\ ... \quad ... \quad ... \quad ... \quad \\ a_{m,1}x_1 + a_{m,2}x_2 + ... a_{m,n}x_n = \; b_m \\ x_1, x_2, ... x_n \ge 0\\ b_1, b_2, ... b_n \ge 0 \end{aligned}\right.$

简言之：

1. 目标函数 $Z$ 最大；
2. 约束条件 $a_{i,1}x_1 + a_{i,2}x_2 + ... a_{i,n}x_n = \; b_i$ 为等式；
3. 决策条件 $x_1, x_2, ... x_n$ 非负
4. 资源限量 $b_1, b_2, ... b_n$ 非负

上方的单纯形法的标准型可以简写成以下形式

$maxZ = \sum_{j=1}^n c_jx_j\\ s.t.\left\{\begin{aligned} \sum_{j=1}^n a_{i,j}x_j = b_j \quad i=1,2,3,...,m\\ x_j \ge 0 \quad j=1,2,3,...,n \end{aligned}\right.$

或写成向量的形式

$maxZ = CX\\ s.t.\left\{\begin{aligned} \sum_{j=1}^n P_jx_j = b \\ x_j \ge 0 \quad j=1,2,3,...,n \\ \end{aligned}\right. \\ 价值向量C = (c_1, c_2, ..., c_n)；\quad 决策变量的向量X = (x_1, x_2, ..., x_n)^T\\ 资源向量b = (b_1, b_2, ..., b_m)^T；\quad 约束条件的系数列向量P_j = (a_{1,j}, a_{2,j}, ..., a_{m,j})$

或写成矩阵的形式

$maxZ = CX\\ s.t.\left\{\begin{aligned} AX = b \\ X \ge O \end{aligned}\right. \\ 其中，A =\begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n}\\ \end{pmatrix}, \quad O =\begin{pmatrix} 0\\ 0\\ \vdots\\ 0\\ \end{pmatrix}, \quad X =\begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{pmatrix}$

一般形式化成标准型

例2：我们需要将以下一般形式化成标准型

$minZ = x_1 + 2x_2 + 3x_3 \quad ① \\ s.t.\left\{\begin{aligned} -2x_1 + x_2 + x_3 \le 9 \quad ②\\ -3x_1 + x_2 + 2x_3 \ge 4 \quad ③\\ 4x_1 - 2x_2 - 3x_3 = -6 \quad ④ \\ x_1 \le 0,\; x_2 \ge 0,\; x_3无约束 \end{aligned}\right.$

1. 【目标函数最大】

   如果目标函数的求解是最小值问题，我们需要将其转换成最大值问题，方法为取负数：

   $min \; Z = CX \quad \stackrel{Z'=-Z}{\Longrightarrow} \quad max\; Z' = -CX$

   所以在例题中：

   $minZ = x_1 + 2x_2 + 3x_3 \quad \stackrel{Z'=-Z}{\Longrightarrow} \quad maxZ' = -x_1 - 2x_2 - 3x_3$

2. 【资源限量非负】

   $b_i < 0 \quad \stackrel{两端同乘(-1)}{\Longrightarrow} \quad 右端项非负\\ b_i = 0\;的情况日后再议$

   我们可以发现，例中的 ④ 式的资源限量为 -6，所以

   $④ \quad 4x_1 - 2x_2 - 3x_3 = -6 \quad \stackrel{两端同乘(-1)}{\Longrightarrow} \quad -4x_1 + 2x_2 + 3x_3 = 6$

3. 【约束条件化为等式】

   $将约束条件中的 \le \quad \stackrel{【加上】松弛变量}{\Longrightarrow} \quad 变成 = \\ 将约束条件中的 \ge \quad \stackrel{【减掉】剩余变量}{\Longrightarrow} \quad 变成 =$

   例如例中的 ② 式，我们需要将其化为等式，则

   $② \quad -2x_1 + x_2 + x_3 \le 9 \quad \stackrel{【加上】松弛变量}{\Longrightarrow} \quad -2x_1 + x_2 + x_3 +x_4 = 9$

   注意⚠️：此时的 $x_4$ 实际上是无意义的，只是我们加入的使等式成立的松弛变量。

   同理，对于 ③ 式，我们有

   $③ \quad -3x_1 + x_2 + 2x_3 \ge 4 \quad \stackrel{【减掉】剩余变量}{\Longrightarrow} \quad -3x_1 + x_2 + 2x_3 - x_5 = 4$

   松弛变量与剩余变量在实际问题中分别表示未被充分利用的资源和超出的资源，均未转化为价值和利润，所以引进模型后它们**在目标函数中的系数均为 0 **。

4. 【决策变量非负】

   $x \le 0 \quad \stackrel{x' = -x}{\Longrightarrow} \quad x' \ge 0$

   例如例题中的 $x_1 \le 0$，我们需要将其化为大于 0 的形式，则

   $x_1 \le 0 \quad \stackrel{x_1' = -x_1}{\Longrightarrow} \quad {x_1}' \ge 0$

   • 【处理无约束变量】

     $x无约束 \quad \stackrel{x = x' -x''}{\Longrightarrow} \quad x'\ge 0,\; x'' \ge 0$

     意为，一个无约束的数 $x$ 可以等于两个非负数 $x',x''$ 的差，其结果依然无约束。但是 $x',x''$ 是存在约束的。

     例如例题中的 $x_3 无约束$，我们将其变化为

     $x_3无约束 \quad \stackrel{x_3 = x_3' -x_3''}{\Longrightarrow} \quad x_3'\ge 0,\; x_3'' \ge 0$

5. 最后请注意替换后的变量代入原式时的替换问题

所以，通过以上步骤，例题中的原式可化为如下形式：

$maxZ = x_1' - 2x_2 - 3x_3' + 3x_3'' + 0x_4 + 0x_5 \quad ① \\ s.t.\left\{\begin{aligned} 2x_1' + x_2 + x_3' - x_3'' + x_4 = 9 \quad ②\\ 3x_1' + x_2 + 2x_3' - 2x_3'' - x_5 = 4 \quad ③\\ -4x_1' + 2x_2 + 3x_3' - 3x_3'' = 6 \quad ④ \\ x_1',\; x_2,\; x_3',\; x_3'',\; x_4,\; x_5 \ge 0 \end{aligned}\right.$

1.1.4 解的概念

可行解 和 最优解

在以下线性规划问题的一般形式中，

$maxZ = \sum_{j=1}^n c_jx_j \qquad ①\\ s.t.\left\{\begin{aligned} \sum_{j=1}^n a_{i,j}x_j = b_j \quad i=1,2,3,...,m \qquad ② \\ x_j \ge 0 \quad j=1,2,3,...,n \qquad ③ \end{aligned}\right.$

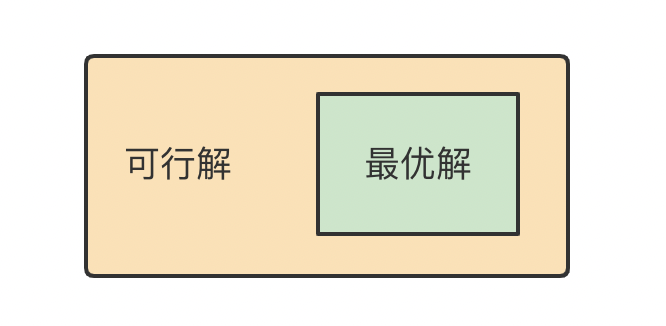
• 【可行解】：满足约束条件 ② 和 ③ 的解。全部可行解的集合称为可行域
• 【最优解】：是目标函数 ① 最大的可行解

基解 和 基可行解

$maxZ = CX\\ s.t.\left\{\begin{aligned} AX = b \\ X \ge O \end{aligned}\right. \\ 其中， C =\begin{pmatrix} c_1\\ c_2\\ \vdots\\ c_n\\ \end{pmatrix}, \quad X =\begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{pmatrix}, \quad A_{m<n} =\begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n}\\ \end{pmatrix}, \quad b =\begin{pmatrix} b_1\\ b_2\\ \vdots\\ b_n\\ \end{pmatrix}, \quad O =\begin{pmatrix} 0\\ 0\\ \vdots\\ 0\\ \end{pmatrix}$

• 【基】：设 $A$ 是约束方程组 ② 的 $m\times n$ 阶系数矩阵（设 $n>m$，变量的个数大于方程的个数，即方程组一定有无穷多个解），其秩(rank) 为 $m$，$B$ 是 $A$ 中的一个 $m\times m$ 阶的满秩子矩阵（行列式 $|B| \ne 0$ 的非奇异子矩阵），称 $B$ 是线性规划问题的一个基。

$R(A) = m \Rightarrow \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,m}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,m}\\ \vdots & \vdots & \vdots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,m}\\ \end{pmatrix} \Rightarrow \begin{pmatrix} P_{1} & P_{2} & \cdots & P_{m} \end{pmatrix},\; 其中 P_i =\begin{pmatrix} a_{1,i}\\ a_{2,i}\\ \vdots\\ a_{m,i}\\ \end{pmatrix}$

• 【基向量组 $B$】（极大线性无关组）：向量组 $A$ 中有 $m$ 个线性无关的向量，且其余向量均可由这 $m$ 个向量来线性表示

$\begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \vdots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n}\\ \end{pmatrix} \times X \Rightarrow \begin{pmatrix} a_{1,1}\\ a_{2,1}\\ \vdots\\ a_{m,1}\\ \end{pmatrix}x_1 + \begin{pmatrix} a_{1,2}\\ a_{2,2}\\ \vdots\\ a_{m,2}\\ \end{pmatrix}x_2 + ...+ \begin{pmatrix} a_{1,n}\\ a_{2,n}\\ \vdots\\ a_{m,n}\\ \end{pmatrix} x_n = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{m}\\ \end{pmatrix}$

设方程组前 $m$ 个变量的系数列向量就是它的基向量（极大线性无关组），则

$\begin{pmatrix} a_{1,1}\\ a_{2,1}\\ \vdots\\ a_{m,1}\\ \end{pmatrix}x_1 + \begin{pmatrix} a_{1,2}\\ a_{2,2}\\ \vdots\\ a_{m,2}\\ \end{pmatrix}x_2 + ...+ \begin{pmatrix} a_{1,n}\\ a_{2,n}\\ \vdots\\ a_{m,n}\\ \end{pmatrix} x_n = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{m}\\ \end{pmatrix} \Rightarrow$

$\begin{pmatrix} a_{1,1}\\ a_{2,1}\\ \vdots\\ a_{m,1}\\ \end{pmatrix}x_1 + \begin{pmatrix} a_{1,2}\\ a_{2,2}\\ \vdots\\ a_{m,2}\\ \end{pmatrix}x_2 + ...+ \begin{pmatrix} a_{1,m}\\ a_{2,m}\\ \vdots\\ a_{m,m}\\ \end{pmatrix} x_m = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{m}\\ \end{pmatrix} - \begin{pmatrix} a_{1,m+1}\\ a_{2,m+1}\\ \vdots\\ a_{m,m+1}\\ \end{pmatrix} x_{m+1} - ... - \begin{pmatrix} a_{1,n}\\ a_{2,n}\\ \vdots\\ a_{m,n}\\ \end{pmatrix} x_n$

其中，$P_1,\;P_2,\;...,\; P_m$ 被称为【基向量】，它们对应的变量 $x_1,\; x_2,\; ...,\; x_m$​ 被称作【基变量】；$P_{m+1},\; ...,\; P_n$ 被称为【非基向量】，它们对应的变量 $x_{m+1},\; ...,\; x_n$ 被称作【非基变量】。

令所有的非基变量 $x_{m+1}=x_{m+2}= ...=x_n = 0$，又因为 $|B| \ne 0$，根据克莱姆法则，可以求出一个唯一解：

$\begin{pmatrix} a_{1,1}\\ a_{2,1}\\ \vdots\\ a_{m,1}\\ \end{pmatrix}x_1 + \begin{pmatrix} a_{1,2}\\ a_{2,2}\\ \vdots\\ a_{m,2}\\ \end{pmatrix}x_2 + ...+ \begin{pmatrix} a_{1,m}\\ a_{2,m}\\ \vdots\\ a_{m,m}\\ \end{pmatrix} x_m = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{m}\\ \end{pmatrix} \quad \stackrel{解得X_B}{\Longrightarrow} \quad \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_m\\ \end{pmatrix}$

【基解】：根据基 $B$ 求得的解 $X$ 被称作基解。

$X = (X_B + X_N) = (x_1,\; x_2,\; ...,\; x_m,\; 0, \; 0, \; ...,\; 0)^T$

其中，

• 基解中非零分量的数目不大于 $m$（方程个数）；
• 有一个基，就能求得一组基解。

【基可行解】：基解中所有分量都满足非负条件的解，即

$X = (X_B + X_N) = (x_1,\; x_2,\; ...,\; x_m,\; 0, \; 0, \; ...,\; 0)^T,\quad x_i \ge 0,i\in1,2,...,n$

【可行即】：对应于基可行解的基，称为可行基。

四个解的关系

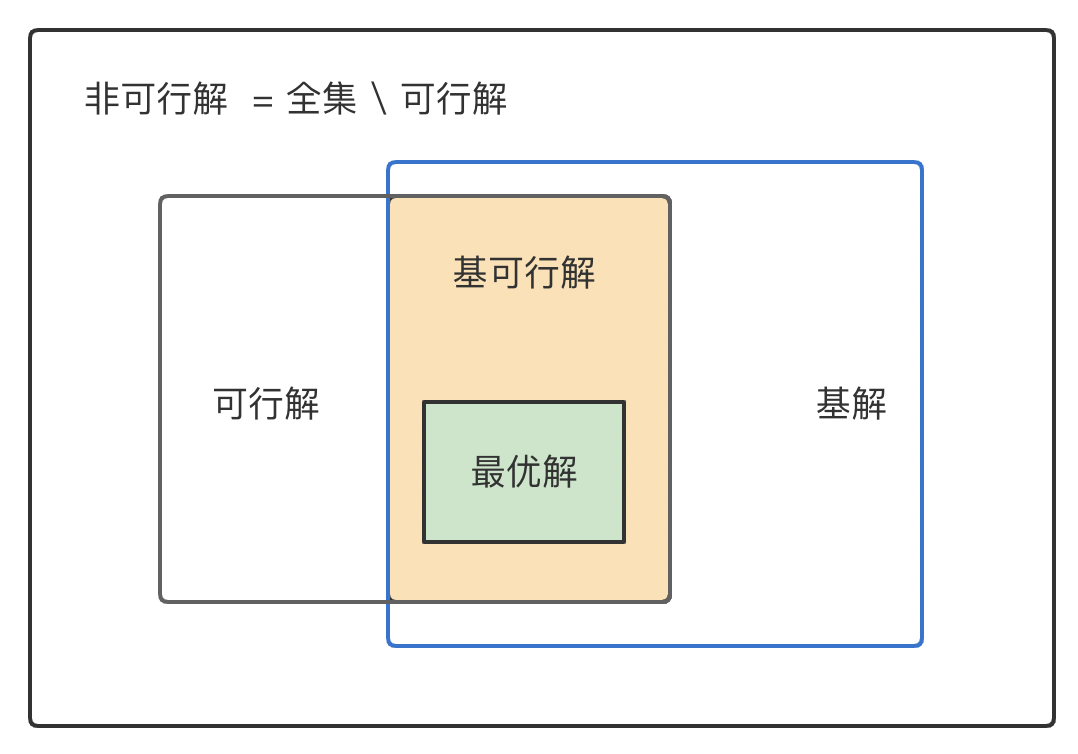
• 当最优解唯一时，最优解也是基可行解；
• 当最优解不唯一时，最优解不一定是基可行解。

1.2 单纯形法

单纯形法的思想

我们继续探究例2，用基的方法求解最优解。在 1.1.3 节的末尾，我们得到了化为标准型的线性规划问题模型：

$maxZ = x_1' - 2x_2 - 3x_3' + 3x_3'' + 0x_4 + 0x_4 \quad ① \\ s.t.\left\{\begin{aligned} 2x_1' + x_2 + x_3' - x_3'' + x_4 = 9 \quad ②\\ 3x_1' + x_2 + 2x_3' - 2x_3'' - x_5 = 4 \quad ③\\ -4x_1' + 2x_2 + 3x_3' - 3x_3'' = 6 \quad ④ \\ x_1',\; x_2,\; x_3',\; x_3'',\; x_4,\; x_5 \ge 0 \end{aligned}\right.$

1. 首先，我们可以将约束条件中的系数矩阵 $A$ 写出来：

   $A =\begin{pmatrix} 2 & 1 & 1 & -1 & 1 & 0\\ 3 & 1 & 2 & -2 & 0 & 1\\ -4 & 2 & 3 & -3 & 0 & 0\\ \end{pmatrix} \Rightarrow \begin{pmatrix} P_{1} & P_{2} & P_3 & P_4 & P_5 & P_{6} \end{pmatrix}$

2. 我们可以看出，这是 $A$ 是一个 $3\times 6$ ，秩为 3 的矩阵，则我们需要找到一个行列式不为 $0$ 的 $3 \times 3$ 的基矩阵 $B$

   $|B_1| = \begin{vmatrix} P_{1} & P_{2} & P_3 \end{vmatrix} = \begin{vmatrix} 2 & 1 & 1 \\ 3 & 1 & 2 \\ -4 & 2 & 3 \\ \end{vmatrix} = -9$

3. 因为 $P_1, P_2, P_3$ 线性无关，令 $\begin{pmatrix}P_{1} & P_{2} & P_3\end{pmatrix}$ 为基，则

   $\begin{pmatrix} 2 & 1 & 1 & -1 & 1 & 0\\ 3 & 1 & 2 & -2 & 0 & 1\\ -4 & 2 & 3 & -3 & 0 & 0\\ \end{pmatrix} \times \begin{pmatrix} x_1'\\ x_2\\ x_3'\\ 0\\ 0\\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ 4 \\ 6 \end{pmatrix} \qquad \Rightarrow \qquad X^{(1)}= \begin{pmatrix} x_1'\\ x_2\\ x_3'\\ 0\\ 0\\ 0 \end{pmatrix} = \begin{pmatrix} 0.7778\\ 13.2222\\ -5.77778\\ 0\\ 0\\ 0 \end{pmatrix}$

4. 求解出的基解有元素小于 0，所以这个基解 $X^{(1)}$不是可行解。

5. 重复第 2 步，找到一个行列式不为 $0$ 的 $3 \times 3$ 的基矩阵 $B_i$，解得它的基解 $X^{(i)}$ 。若 $X^{(i)}$ 的所有元素都满足非负约束（$\ge 0$），则 $X^{(i)}$ 就是可行解。

   • 【出基】：将列向量 $P_i$ 从基里移除，即

     $B_i = \begin{pmatrix} P_{a} & P_{i} & P_{b} \end{pmatrix} = \begin{pmatrix} a_{1,a} & a_{1,i} & a_{1,b} \\ a_{2,a} & a_{2,i} & a_{2,b} \\ a_{3,a} & a_{3,i} & a_{3,b} \\ \end{pmatrix} \quad \stackrel{P_i出基}{\Longrightarrow} \quad \begin{pmatrix} P_{a} & P_{b} \end{pmatrix} = \begin{pmatrix} a_{1,a} & a_{1,b} \\ a_{2,a} & a_{2,b} \\ a_{3,a} & a_{3,b} \\ \end{pmatrix}$

     【进基】：将列向量 $P_j$ 移进基中，即

     $B_j = \begin{pmatrix} P_{a} & P_{b} \end{pmatrix} = \begin{pmatrix} a_{1,a} & a_{1,b} \\ a_{2,a} & a_{2,b} \\ a_{3,a} & a_{3,b} \\ \end{pmatrix} \quad \stackrel{P_j进基}{\Longrightarrow} \quad \begin{pmatrix} P_{a} & P_{j} & P_{b} \end{pmatrix} = \begin{pmatrix} a_{1,a} & a_{1,j} & a_{1,b} \\ a_{2,a} & a_{2,j} & a_{2,b} \\ a_{3,a} & a_{3,j} & a_{3,b} \\ \end{pmatrix}$

     尽量选择目标函数里对结果影响大的向量【进基】，因为我们不希望它是非基向量而使其基变量为 0；尽量选择“容量”最小的列向量【出基】

6. 解出所有的基解 $X^{(n)}$，其中基解的数目 $n \le C_6^4=15$ 个。找出所有基解中的可行解

7. 再将所有可行解代入目标函数 ① 中，结果最大的就是【最优解】

单纯形法的计算步骤

• 为了书写规范和便于计算，对单纯形法的计算设计了【单纯形表】
• 每一次迭代对应一张单纯形表
• 含初始基可行解的单纯形表称为【初始单纯形表】
• 含最优解的单纯形表称为【最终单纯形表】

单纯形表

单纯形表解题方法：

1. 将题目给出的线性规划问题化为标准型
2. 根据标准型填写初始单纯形表
   • 列数： $未知数\;x_i\;的个数+ c_B + X_B + b + \theta_i$
   • 行数：$约束方程的个数 + c_j + \sigma_j$
   • $c_j$：目标函数中各个变量的系数，对应地填入表内
   • 每个变量所在列的数字根据大括号中约束方程组中该变量的系数
   • 【基】找出变量下放已填写数字构成的矩阵中的单位矩阵，依次将该单位矩阵对应的变量写在 $X_B$ 的下面
   • 将上一步骤中找到的变量上方的数字 $c_j$ 依次对应地填入 $c_B$ 中
   • 将大括号中约束方程组等号右边的 $b_i$ 依次填到 $b$ 下面
3. 找出可行解
   • 令 $X_B$ 所在列的变量与**$b$ 所在列的数字**对应相等，再令其他变量等于 0
4. 求出检验数 $\sigma_j = c_j -(c_{B_1}x_{j1} + c_{B_2}x_{j2} + ...)$
   • $X_B$ 下面的变量对应的 $\sigma$ 的值为 0
   • 【初始单纯形表】中 $c_j$ 的数字与 $\sigma_j$ 行的数字完全相同
5. 观察一下 $\sigma_j$ 这一行的数字看一下是否都 $≤0$
   • 若这些数字都 $≤0$，则该可行解就是最优解
   • 若这些数字有＞0的，则该可行解不是最优解，继续进行步骤 6
6. 找到 $\sigma_j$ 行最大的数字 $max(\sigma_j)$ 那一列对应的变量 $x_a$【进基变量】，求出 $\theta _{i} = {b_i}/{x_{ai}}$：
   • 若 $\theta \ge 0$，则把 $\theta$ 的值填到表中
   • 若 $\theta < 0$，则不用把 $\theta$ 的值填到表中
   • 若 $\theta \; 无意义$，则不用把 $\theta$ 的值填到表中
7. 找到表中 $\theta _i$ 最小值对应 $X_B$ 列的变量 $x_b$（出基变量），找到【 $x_a$ 的列】和 【$x_b$ 的行】交叉的数字 $m$
8. 用 【$x_a$ 上面的数字 $c_a】$ 替代 【$x_b$ 前面的数字 $c_b$】，用 $x_a$ 替代 $x_b$，清空 $\sigma_j$ 行与 $\theta_i$ 列
9. 对 $x_1,x_2…x_n$ 与 $b$ 列组成的矩阵进行运算，【将 $m$ 变成 $1$】（矩阵的初等行变换），同列其他元素变成 $0$，形成一个新的矩阵，将该矩阵中的数字填入表格中对应的位置形成新的单纯形表并进行步骤 3
10. 如何检验所求的最优解是不是唯一最优解：
    • 找出 $X_B$ 列变量以外的变量
    • 找出 $X_B$ 列变量以外的变量对应的 $\sigma_i$
    • 若 $X_B$ 列变量以外的变量对应的 $\sigma_i$ 都 $＜0$，则 $X^*$ 为唯一最优解
    • 若 $X_B$ 列变量以外的变量对应的 $\sigma_i$ 中有 $=0$ 的，则 $X^*$ 是无穷多最优解中的一个

【例】给出下列问题：

$max Z = 2x_1 + 3x_2 + 0x_3 + 0x_4 + 0x_5 \quad ① \\ s.t.\left\{\begin{aligned} x_1 + 2x_2 + x_3 + 0x_4+ 0x_5 = 8 \quad ②\\ 4x_1 + 0x_2 + 0x_3 + x_4 + 0x_5 = 16 \quad ③\\ 0x_1 + 4x_2 + 0x_3+ 0x_4+ x_5 = 12 \quad ④ \\ x_1, x_2, x_3, x_4, x_5 \ge 0 \end{aligned}\right.$

1. 该线性规划问题已化成标准形式；

2. 根据标准型填写如下的初始单纯形表。

   \	$c_j:$	2	3	0	0	0	\	\
   $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
   0	$x_3$	1	2	1	0	0	8	4
   0	$x_4$	4	0	0	1	0	16	❌
   0	$x_5$	0	4	0	0	1	12	3
   \	$\sigma_i:$	2	3	0	0	0	\	\

3. 找出可行解：令 $X_B$ 所在列的变量与**$b$ 所在列的数字**对应相等，再令其他变量等于 0。故

   $X^{(0)} = (x_3 = 8, x_4 = 16, x_5 = 12, x_1 =0 , x_2 =0) \quad \stackrel{整理}{\Longrightarrow} \quad X^{(0)}=(0,0,8,16,12)^T$

4. 求出检验数 $\sigma_j = c_j -(c_{B_1}x_{j1} + c_{B_2}x_{j2} + ...)$ :

   • $\sigma_1 = c_1 -(c_{B_1}x_{11} + c_{B_2}x_{12} + c_{B_3}x_{13}) = 2-(0\times 1+0\times 4+0\times0) = 2$
   • $\sigma_2 = c_2 -(c_{B_1}x_{21} + c_{B_2}x_{22} + c_{B_3}x_{23}) = 3-(0\times 2+0\times 0+0\times4) = 3$
   • $\sigma_3 = c_3 -(c_{B_1}x_{31} + c_{B_2}x_{32} + c_{B_3}x_{33}) = 0-(0\times 1+0\times 0+0\times0) = 0$
   • $\sigma_4 = c_4 -(c_{B_1}x_{41} + c_{B_2}x_{42} + c_{B_3}x_{43}) = 0-(0\times 0+0\times 1 + 0\times0) = 0$
   • $\sigma_5 = c_5 -(c_{B_1}x_{51} + c_{B_2}x_{52} + c_{B_3}x_{53}) = 0-(0\times 0+0\times 0+0\times1) = 0$

5. 观察一下 $\sigma_j$ 这一行的数字看一下是否都 $≤0$ ？否，继续进行下一步。

6. 找到 $\sigma_j$ 行最大的数字 $max(\sigma_j)$ 那一列对应的变量 $x_a$【进基变量】，求出 $\theta _{i} = {b_i}/{x_{ai}}$：

   $max(\sigma_j) = 3 =\theta_2 \quad \stackrel{对应的}{\Longrightarrow} \quad 进基变量x_a = x_2$

   • $\theta _{1} = {b_1}/{x_{21}} = 8 / 2 = 4 >0$，填入表中
   • $\theta _{2} = {b_2}/{x_{22}} = 16 / 0 :无意义$
   • $\theta _{3} = {b_3}/{x_{31}} = 12 / 4 = 3 >0$，填入表中

7. 找到表中 $\theta _i$ 最小值对应 $X_B$ 列的变量 $x_b$【出基变量】，找到 $x_a$ 的列和 $x_b$ 的行交叉的数字 $m$：

   $min(\theta_i) = 3 = \theta_3 \quad \stackrel{对应的}{\Longrightarrow} \quad 出基变量 x_b = x_5$。$x_a = x_2$的列 与 $x_b = x_5$ 的行交叉的数字 $m = 4$

8. 用 $x_a$ 上面的数字替代 $x_b$ 前面的数字，用 $x_a$ 替代 $x_b$，清空 $\sigma_j$ 行与 $\theta_i$ 列：

   \	$c_j:$	2	3	0	0	0	\	\
   $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
   0	$x_3$	1	2	1	0	0	8
   0	$x_4$	4	0	0	1	0	16
   3	$x_2$	0	4	0	0	1	12
   \	$\sigma_i:$						\	\

9. 对 $x_1,x_2…x_n$ 与 $b$ 列组成的矩阵进行运算，将 $m$ 变成 $1$，同列其他元素变成 $0$，形成一个新的矩阵，将该矩阵中的数字填入表格中对应的位置形成新的单纯形表并进行步骤 3：

   $M = (x_1,x_2…x_n|b) =(A|b) =\begin{pmatrix} 1 & 2 & 1 & 0 & 0 & 8\\ 4 & 0 & 0 & 1 & 0 & 16\\ 0 & 4 & 0 & 0 & 1 & 12\\ \end{pmatrix}\\ \quad \xrightarrow[1/4 \times 第3行]{m=1的初等行变换} \quad \begin{pmatrix} 1 & 2 & 1 & 0 & 0 & 8\\ 4 & 0 & 0 & 1 & 0 & 16\\ 0 & 1 & 0 & 0 & 1/4 & 3\\ \end{pmatrix}\\ \quad \xrightarrow[第1行+(-2)\times第3行]{m所在列其他元素为0} \quad \begin{pmatrix} 1 & 0 & 1 & 0 & -1/2 & 2\\ 4 & 0 & 0 & 1 & 0 & 16\\ 0 & 1 & 0 & 0 & 1/4 & 3\\ \end{pmatrix}\\$

   \	$c_j:$	2	3	0	0	0	\	\
   $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
   0	$x_3$	1	0	1	0	-1/2	2
   0	$x_4$	4	0	0	1	0	16
   3	$x_2$	0	1	0	0	1/4	3
   \	$\sigma_i:$						\	\

   重复步骤 3 …

10. 经过多次迭代，列出每次迭代过后的单纯形表：

    • 第一次迭代：

      \	$c_j:$	2	3	0	0	0	\	\
      $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
      0	$x_3$	1	2	1	0	0	8	4
      0	$x_4$	4	0	0	1	0	16	❌
      0	$x_5$	0	4	0	0	1	12	3
      \	$\sigma_i:$	2	3	0	0	0	\	\

      $X^{(0)}=(0,0,8,16,12)^T$

    • 第二次迭代：

      \	$c_j:$	2	3	0	0	0	\	\
      $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
      0	$x_3$	1	0	1	0	-1/2	2	2
      0	$x_4$	4	0	0	1	0	16	4
      3	$x_2$	0	1	0	0	1/4	3	❌
      \	$\sigma_i:$	2	0	0	0	-3/4	\	\

      $X^{(1)}=(0,3,2,16,0)^T$

    • 第三次迭代：

      \	$c_j:$	2	3	0	0	0	\	\
      $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
      2	$x_1$	1	0	1	0	-1/2	2	❌
      0	$x_4$	0	0	-4	1	2	8	4
      3	$x_2$	0	1	0	0	1/4	3	12
      \	$\sigma_i:$	0	0	-2	0	1/4	\	\

      $X^{(2)}=(2,3,0,8,0)^T$

    • 第四次迭代：

      \	$c_j:$	2	3	0	0	0	\	\
      $c_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$b$	$\theta_i$
      2	$x_1$	1	0	0	0	1/4	4
      0	$x_5$	0	0	-2	1/2	1	4
      3	$x_2$	0	1	1/2	-1/8	0	2
      \	$\sigma_i:$	0	0	-3/2	-1/8	0	\	\

      $X^{(3)}=(4,2,0,0,4)^T$

      我们观察观察一下 $\sigma_j$ 这一行的数字看一下是否都 $≤0$？是，则该可行解就是最优解，即$X^* = X^{(3)}=(4,2,0,0,4)^T$

      所以，$max Z = 2x_1 + 3x_2 + 0x_3 + 0x_4 + 0x_5 = 14$

第二部分：整数线性规划

整数线性规划模型是在一般线性规划模型的基础上加上决策变量取整数值的约束，由此，我们可以得到整数线性规划问题的一般形式如下：

$maxZ = \sum_{j=1}^n c_jx_j \qquad ①\\ s.t.\left\{\begin{aligned} \sum_{j=1}^n a_{i,j}x_j = b_j \quad i=1,2,3,...,m \qquad ② \\ x_j \ge 0 \quad j=1,2,3,...,n \qquad ③\\ x_1,x_2,x_3,...,x_n \in \Z \qquad ④ \end{aligned}\right.$

1. 先不考虑 $x \in \Z$，求解问题；
2. 再不考虑 $x \in \Z$，结合 1 中的解，找到最优解。

实际上，整数线性规划根据决策变量取整数的情况可以进行如下区分：

• 混合整数规划 ＆ 全整数规划

• 0-1型整数规划 ＆ 非0-1型整数规

含 0-1 变量的建模

对不含0-1变量的整数规划问题，我们只需要按照一般线性规划问题的形式进行建模，然后综合问题的性质给相应变量增加取整的约束即可；但对于包含0-1变量的问题，由于0-1变量作为二进制变量（或逻辑量），其应用性很强，在实际问题的建模中常常需要灵活运用。

• 表示系统是否处于某个特定状态，或决策时是否取某个特定方案，如

  $x =\left\{\begin{aligned} 1 \qquad \qquad决策取方案P时 \\ 0 \qquad 决策不取方案P时(\bar P) \\ \end{aligned}\right.$

• 当问题含多项要素，每项要素面临两种选择时，可用0-1变量来描述。
  设问题有有限项要素 $E_1, E_2,...,E_n$，其中每项E，有两种选择 $A_j$ 和 $\bar A_j (j=1,2,...,n)$，可令：

  $x_j =\left\{\begin{aligned} 1 \qquad 若E_j选择A_j \\ 0 \qquad 若E_j选择\bar A_j \\ \end{aligned}\right.$

含有相互排斥的约束条件的问题

我们可以设两个 0-1 变量 $y_1,y_2$:

$y_1 =\left\{\begin{aligned} 1 \qquad 若E_j选择A_j \\ 0 \qquad 若E_j选择\bar A_j \\ \end{aligned}\right.$

分支定界法

可以理解为“二分比较”，对可行域进行二分，如果在当前可行域内有最优解

$maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \quad x_1,x_2\in \Z \qquad ④ \end{aligned}\right.$

1. 我们先设不考虑 $x_1,x_2\in \Z$ 的情况为B问题：

   $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④ \end{aligned}\right.$

2. 运用单纯形法，我们可以得出B问题的最优解 $X_B^* = (4.81,\;1.82)^T$，$maxZ_B = 356$

3. 我们可以根据整数对可行域进行二分，然后再讨论：

   • 不考虑 $x_1,x_2\in \Z$ 的情况下 $x_1^* = 4.81$，所以我们可以在左右两边对区域进行划分，即 $x_1 \le 4$ 和 $x_1 \ge 5$ ，将新得到的约束分别加入到 B 问题中

     (1) 问题 $B_1$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \le 4 \qquad ⑤ \end{aligned}\right.$

     运用单纯形法，我们可以得出 $B_1$ 问题的最优解 ${X_B}_1^* = (4,\;2.1)^T$，$max{Z_B}_1 = 349$

     我们可以在 $x_2$ 左右两边对区域进行划分，即 $x_2 \le 2$ 和 $x_2 \ge 3$ ，将新得到的约束分别加入到 $B_1$ 问题中：

     ​ (i) 问题 $B_{11}$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \le 4 \qquad ⑤\\ x_2 \le 2 \qquad ⑥ \end{aligned}\right.$

     ​ 运用单纯形法，我们可以得出 $B_1$ 问题的最优解 ${X_B}_{11}^* = (4,\;2)^T$，$max{Z_B}_{11} = 340$

     ​ (ii) 问题 $B_{12}$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \le 4 \qquad ⑤\\ x_2 \ge 3 \qquad ⑥ \end{aligned}\right.$

     ​ 运用单纯形法，我们可以得出 $B_1$ 问题的最优解 ${X_B}_{12}^* = (1.42,\;3)^T$，$max{Z_B}_{12} = 327$

     (2) 问题 $B_2$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \ge 5 \qquad ⑤ \end{aligned}\right.$

     运用单纯形法，我们可以得出 $B_2$ 问题的最优解 ${X_B}_2^* = (5,\;1.57)^T$，$max{Z_B}_2 = 341$

     我们可以在 $x_2$ 左右两边对区域进行划分，即 $x_2 \le 1$ 和 $x_2 \ge 2$ ，将新得到的约束分别加入到 $B_2$ 问题中：

     ​ (i) 问题 $B_{21}$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \ge 5 \qquad ⑤\\ x_2 \le 1 \qquad ⑥ \end{aligned}\right.$

     ​ 运用单纯形法，我们可以得出 $B_1$ 问题的最优解 ${X_B}_{21}^* = (5.44,\;1)^T$，$max{Z_B}_{21} = 308$

     ​ (ii) 问题 $B_{22}$

     $maxZ = 40x_1 + 90x_2 \qquad ①\\ s.t.\left\{\begin{aligned} 9x_1 +7x_2 \le 56\qquad ② \\ 7x_1 + 20x_2 \le 70 \qquad ③\\ x_1,x_2 \ge 0 \qquad ④\\ x_1 \ge 5 \qquad ⑤\\ x_2 \ge 2 \qquad ⑥ \end{aligned}\right.$

     ​ 运用单纯形法，我们可以得出 $B_1$ 问题的最优解 ${X_B}_{22}^*无可行解$

第三部分：动态规划

我们有如下问题，给定一个线路网络，两点之间连线上的数字表示两点间的距离（或费用），试求一段由 A 到 E 的管线铺路，使总距离为最短（或总费用最小）。

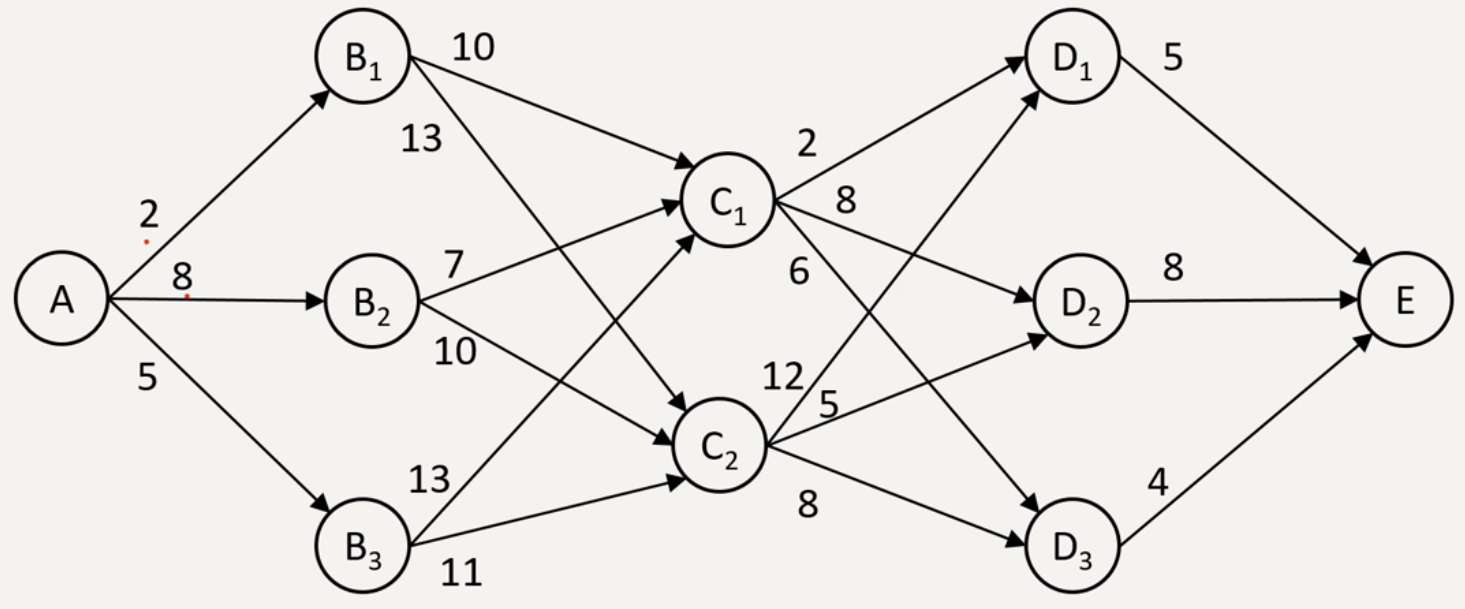
其实从A到E并不是一次性的决策，$A \to B, \quad B \to C, \quad C\to D, \quad D \to E$。

由此我们可见，将问题分成若干相互联系的阶段，在每个阶段都需要做出决策，使全过程达到整体最优，这类问题我们称为多阶段决策问题（资源分配、生产存储）。最大特点就是可以把问题拆分成很多阶段。

基本概念

• 阶段：将问题划分成若干个相互联系的阶段。$k$ 表示为阶段变量。

  上图有四个阶段，分别是：$A \to B, \quad B \to C, \quad C\to D, \quad D \to E$

• 状态：每个阶段开始时所处的自然状态。$s_k$ 表示为状态变量。

  上图有10个状态，分别是：$A,\qquad B_1,B_2,B_3 \qquad C_1,C_2 \qquad D_1,D_2,D_3 \qquad E$

• 决策：当过程处于某一阶段的某一状态时作出的决定，从而确定下一阶段的状态。$x_k$ 表示为决策变量。

  • 允许决策集合：决策变量的取值范围。$D_k(s_k)$ 表示第k阶段从状态$s_k$ 出发的允许决策集合。$x_k \in D_k(s_k)$

• 策略：按顺序排列的决策集合。

• 状态转移方程：确定过程由一个状态到另一个状态的演变过程。$S_{k+1} = T_k(S_k,x_k)$。

• 指标函数：衡量所实现过程优劣的数值指标

  • 阶段指标函数 $v_k(S_k,x_k)$ ：从k阶段状态 $s_k$ 出发，选择决策 $x_k$ 所产生的第k阶段指标
  • 过程指标函数 $V_k(S_k,x_k,x_{k+1},...,x_n)$：从k阶段状态 $S_k$ 出发，选择决策 $x_k,x_{k+1},...,x_n$ 所产生的过程指标
    • $V_k(s_k,x_k,x_{k+1},...,x_n) = V[v_k(s_k,x_k),V_{k+1}(S_{k+1},x_{x+1},...,x_n)]$

• 最优值函数 $f_x(S_k)= \text{min/max}_{x_k\in D_k(S_k)} \quad V_k(s_k,x_k,x_{k+1},...,x_n)$

	连和形式	连乘形式
指标函数	$V_k(S_k,x_k,x_{k+1},...,x_n) = \sum _{j=k}^{n-1}v_j(s_j,x_j)+V_n$	$V_k(S_k,x_k,x_{k+1},...,x_n) = \prod _{j=k}^{n-1}v_j(s_j,x_j)+V_n$
最优值函数	$f_x(S_k)= \text{min/max}_{x_k\in D_k(S_k)} \quad V_k(s_k,x_k,x_{k+1},...,x_n)$
动态规划模型

基本原理

1. 最优性原理：一个最优策略的子策略也是最优的。

例如：已知最优策略为 $A \to B_1 \to C_1 \to D_1 \to E$，则 $C \to E$ 的最优策略为 $C_1 \to D_1 \to E$ 。

2. 无后效性原理：如果某阶段的状态给定之后，在此阶段以后过程的发展不受这个阶段以前各个状态的影响

我们以上图为例：

阶段 $k$：$k=1,2,3,4$

状态变量 $S_k$：$S_1=\{A\} \quad S_1=\{A\} \quad S_2=\{B_1,B_2,B_3\} \quad S_3=\{C_1,C_2\} \quad S_4=\{D_1,D_2,D_3\} \quad S_5=\{E\}$

决策变量 $x_k$ ：$S_k$ 状态时选择到达下一阶段的点

允许决策集合：$x_k \in D_k(S_k)$

状态指标函数 $v_k(S_k,x_k)$：状态点 $S_k$ 到决策点 $x_k$ 间的最短距离

最优指标函数 $f_k(S_k)$：k阶段状态为 $S_k$ 时到终点 $E$ 间的最短距离

递推方程：$\left\{\begin{aligned} f_x(S_k)= \text{min}_{x_k\in D_k(S_k)} \quad \{v_k(s_k,x_k)+f_{k+1}(S_{k+1})\}, k=1,2,3,4 \\ f_{5}(S_{5})=0 \\ \end{aligned}\right.$