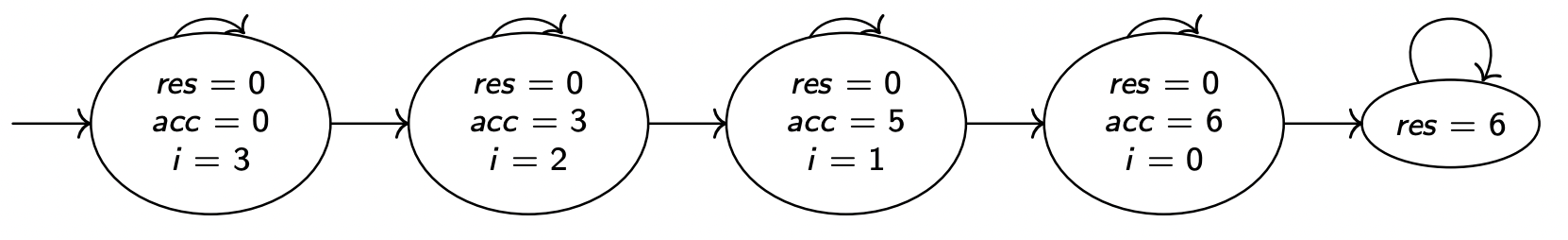本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第八学期课程“Système de Transition”总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
参考:
在计算机科学和控制理论中,“变迁系统”用数学的方法描述离散系统的行为。变迁系统主要由“状态”和状态之间的“状态迁移”组成。 有标号的变迁系统可以从已定义的标签集合中选择相应标签来标记状态迁移,而且相同的标签可能被应用在多个状态迁移上。 变迁系统也可以是无标记的,此时也可以认为标签集合中只有单一标签元素,从而省略了状态迁移上的标签记号。
变迁系统在数学定义上和有向图 一致,但与有限状态自动机 有一定不同。
变迁系统的特点有:
系统状态的集合不一定是有限的或可数的;
状态迁移的集合不一定是有限的或可数的;
变迁系统并不需要给出“开始”状态或“最终”状态;
变迁系统可以表示为有向图 ,有限状态自动机则不能。
资料来源于维基百科:变迁系统
形式化验证技术想要解决的核心问题是:软件总是可能存在 Bug 的,而测试始终无法涵盖所有可能性,特别是对于并发系统及分布式系统来说,就算单元测试达到了 100% 分支覆盖率,也不能肯定的说这个系统在线程安全,一致性等方面不会出问题。那如何更好的来验证我们的程序是否符合预期呢?
形式化验证就旨在使用严谨的数学证明方法来证明某一算法是正确的。
T emporal L ogic of A ctions **+**是由Leslie Lamport 开发的一种【形式化验证语言】。它用于设计、建模、记录和验证程序,尤其是并发系统和分布式系统。TLA +被描述为可完全测试的伪代码,其用途类似于为软件系统绘制蓝图。
由于 TLA+ 写的代码并不是用来实际运行的,故一般将其代码称为模型(Model)而非程序(Program)。
Learn TLA+ L. Lamport 关于TLA+的视频 其他资源
Transition System在计算机科学中通常用作描述系统行为的模型,它是一种有向图,节点代表状态,边代表着状态的转化。
状态(state)描述了系统在其行为的特定时刻的一些信息。
转变(transition)指定系统如何从一种状态演变为另一种状态。
下面给出一种Transition System(TS)的定义
变迁系统是一个三元组⟨ S , I , R ⟩ ⟨S,I,R⟩ ⟨ S , I , R ⟩
S S S 终结状态 和 非终结状态 I ⊆ S I \subseteq S I ⊆ S 初始状态 R ⊆ S × S R \subseteq S \times S R ⊆ S × S ( s , s ′ ) ∈ R (s,s') \in R ( s , s ′ ) ∈ R s s s s ′ s' s ′ s s s s s s s ′ s' s ′ s ′ s' s ′
例:
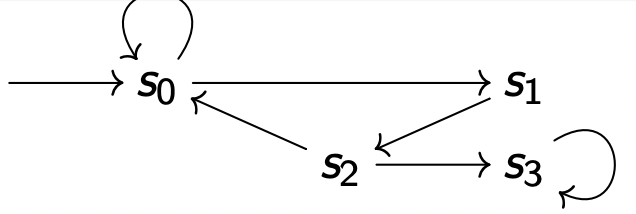
S = S 0 , S 1 , S 2 , S 3 , S 4 S = {S_0, S_1, S_2, S_3,S_4}
S = S 0 , S 1 , S 2 , S 3 , S 4
I = S 0 I = {S_0}
I = S 0
R = { ( S 0 , S 0 ) , ( S 0 , S 1 ) , ( S 0 , S 2 ) , ( S 2 , S 3 ) , ( S 3 , S 4 ) , ( S 4 , S 3 ) } R = \{(S_0,S_0), (S_0,S_1), (S_0,S_2), (S_2,S_3), (S_3,S_4), (S_4,S_3)\}
R = { ( S 0 , S 0 ) , ( S 0 , S 1 ) , ( S 0 , S 2 ) , ( S 2 , S 3 ) , ( S 3 , S 4 ) , ( S 4 , S 3 ) }
定义为:
P o s t ( s , α ) = { s ′ ∈ S ∣ s → α s ′ } Post(s,α)=\{s'∈S | s\xrightarrow{α}s' \}
P o s t ( s , α ) = { s ′ ∈ S ∣ s α s ′ }
就是指状态s s s α α α
如果α为任意动作,可以记为:
P o s t ( s ) = ⋃ α ∈ A c t P o s t ( s , α ) Post(s)=\bigcup_{α∈Act}Post(s,α)
P o s t ( s ) = α ∈ A c t ⋃ P o s t ( s , α )
P r e ( s , α ) = { s ′ ∈ S ∣ s ′ → α s } Pre(s, α) =\{s'∈S|s'\xrightarrow{α}s\}
P r e ( s , α ) = { s ′ ∈ S ∣ s ′ α s }
指通过执行动作α之后能达到状态s的状态集合
同理,α如果为任意动作,则记为:
P r e ( s ) = ⋃ α ∈ A c t P r e ( s , α ) Pre(s)=\bigcup_{α∈Act}Pre(s,α)
P r e ( s ) = α ∈ A c t ⋃ P r e ( s , α )
用图来表示前任和后继的话就是这样子的:
对于TS模型来说,终止状态就是指没有后继状态的状态,即P o s t ( s ) = ∅ Post(s)=\varnothing P o s t ( s ) = ∅
串行程序的终止状态代表着程序的终止。
对于并行程序来说,我们一般不考虑它的终止状态,因为并行程序大都要求持续运行下去。
如果
∣ S 0 ∣ ≤ 1 a n d ∣ P o s t ( s , α ) ∣ ≤ 1 |S_{0}|≤1\;and\;|Post(s,α)|≤1
∣ S 0 ∣ ≤ 1 a n d ∣ P o s t ( s , α ) ∣ ≤ 1
那么这个TS就可以称为动作确定的TS
如果
∣ S 0 ∣ ≤ 1 a n d ∣ P o s t ( s , α ) ∩ { s ′ ∈ S ∣ L ( s ′ ) = A } ∣ ≤ 1 ( A ∈ 2 A P ) |S_{0}|≤1\;and\;|Post(s,α)\cap \{s'∈S|L(s')=A\}|≤1(A∈2^{AP})
∣ S 0 ∣ ≤ 1 a n d ∣ P o s t ( s , α ) ∩ { s ′ ∈ S ∣ L ( s ′ ) = A } ∣ ≤ 1 ( A ∈ 2 A P )
那么这个TS就可以称为AP确定的TS
S S S
S ∗ S^* S ∗ S S S 有限序列集 ;S w S^w S w S S S 无限数据集 ;σ i \sigma _i σ i σ \sigma σ i i i 序列 S S S ⟨ s 1 → s 2 → . . . ⟩ ⟨s1 → s2 → ...⟩ ⟨ s 1 → s 2 → . . . ⟩
⟨ ⟩ ⟨⟩ ⟨ ⟩
对于一个有限序列σ \sigma σ
σ ∗ \sigma^* σ ∗ 有限序列集 。σ + ≜ σ ∗ \ { ⟨ ⟩ } \sigma^+ \triangleq \sigma^* \backslash \{ ⟨⟩ \} σ + ≜ σ ∗ \ { ⟨ ⟩ } σ w \sigma^w σ w
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ σ ∈ S ∗ \sigma \in S^* σ ∈ S ∗
σ = ⟨ s 0 → s 1 → . . . → s n − 1 → s n ⟩ \sigma = ⟨s_0 → s_1 → ... → s_{n-1} → s_n ⟩ σ = ⟨ s 0 → s 1 → . . . → s n − 1 → s n ⟩
∀ i ∈ [ 0... n [ : ( s i , s i − 1 ) ∈ R \forall i \in [0 ... n[:(s_i, s_{i-1}) \in R ∀ i ∈ [ 0 . . . n [ : ( s i , s i − 1 ) ∈ R
当有限轨迹⟨ s 0 → s 1 → . . . → s n − 1 → s n ⟩ ∈ S ∗ ⟨s_0 → s_1 → ... → s_{n-1} → s_n ⟩ \in S^* ⟨ s 0 → s 1 → . . . → s n − 1 → s n ⟩ ∈ S ∗ s n s_n s n ∀ s ∈ S : ( s n , s ) ∉ R \forall s \in S:(s_n, s) \notin R ∀ s ∈ S : ( s n , s ) ∈ / R
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ s 0 ∈ S s_0 \in S s 0 ∈ S s 0 s_0 s 0 t r ∈ S w tr \in S^w t r ∈ S w
t r = ⟨ s 0 → s 1 → s 2 → . . . ⟩ tr = ⟨s_0 → s_1 → s_2 → ... ⟩ t r = ⟨ s 0 → s 1 → s 2 → . . . ⟩
∀ i ∈ N : ( s i , s i + 1 ) ∈ R \forall i \in \mathbb{N}:(s_i, s_{i+1}) \in R ∀ i ∈ N : ( s i , s i + 1 ) ∈ R
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ s ∈ S s \in S s ∈ S
$Traces(s) $ 是从状态s s s
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩
一次执行片段 $σ = ⟨s_0 →…⟩ $ 是满足 $s_0 ∈ I $ 的最大无限或有限轨迹(如果是有限执行片段,那么它结束于终止状态,或者该片段是一个无限执行片段)。
E x e c ( S ) Exec(S) E x e c ( S ) S = ⋃ s 0 ∈ I T r a c e s ( s 0 ) S = \bigcup_{s_0 \in I} Traces(s_0) S = ⋃ s 0 ∈ I T r a c e s ( s 0 ) 如果 I = ∅ I = ∅ I = ∅
如果一个初始、有限执行片段的终止状态为s,那么s称为可达的 (reachable),直观来说,可达表示从初始状态开始能够到达某个状态。我们把所有的可达状态记为Reach(TS)
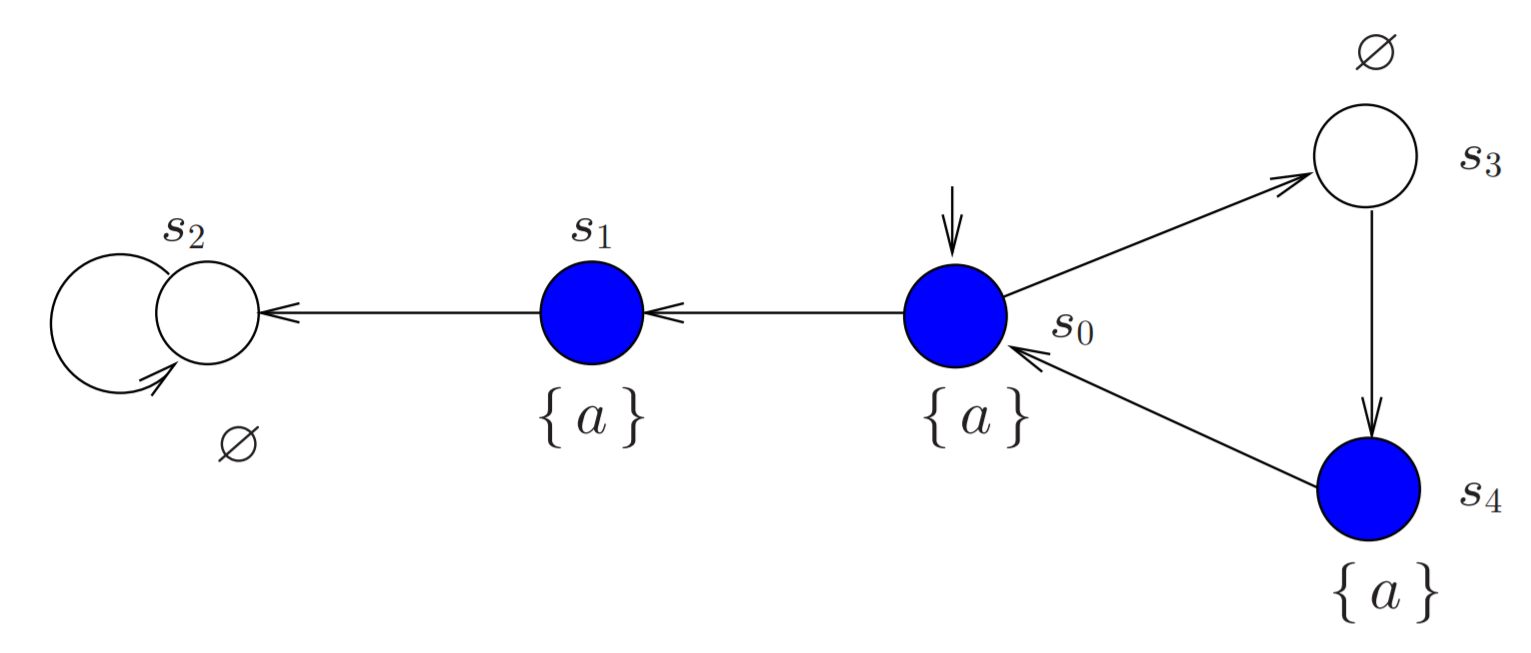
s 0 → s 0 → s 2 → s 3 s_0 → s_0 → s_2 → s_3 s 0 → s 0 → s 2 → s 3
T r a c e s ( s 1 ) = ⟨ s 1 ⟩ Traces(s_1) = ⟨s_1⟩ T r a c e s ( s 1 ) = ⟨ s 1 ⟩ T r a c e s ( s 3 ) = ⟨ ( s 3 → s 4 ) w ⟩ Traces(s_3) = ⟨(s_3 → s_4)^w⟩ T r a c e s ( s 3 ) = ⟨ ( s 3 → s 4 ) w ⟩ T r a c e s ( s 2 ) = ⟨ s 2 → ( s 3 → s 4 ) w ⟩ Traces(s_2) = ⟨s_2 → (s_3 → s_4)^w⟩ T r a c e s ( s 2 ) = ⟨ s 2 → ( s 3 → s 4 ) w ⟩ T r a c e s ( s 0 ) = ⟨ s 0 w ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 → s 2 → ( s 3 → s 4 ) w ⟩ Traces(s_0) = ⟨{s_0}^w⟩, ⟨{s_0}^+ → s_1⟩, ⟨s_0 → s_2 → (s_3 → s_4)^w⟩ T r a c e s ( s 0 ) = ⟨ s 0 w ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 → s 2 → ( s 3 → s 4 ) w ⟩ E x e c ( S ) = T r a c e s ( s 0 ) Exec(S) = Traces(s_0) E x e c ( S ) = T r a c e s ( s 0 )
T r a c e s ( s 2 ) = ⟨ s 2 → s 4 ⟩ , ⟨ ( s 2 → s 3 → s 0 → s 1 ) w ⟩ , ⟨ ( s 2 → s 3 → s 0 → s 1 ) ∗ → s 2 → s 4 ⟩ Traces(s_2) = ⟨s_2 → s_4⟩, ⟨(s_2 → s_3 → s_0 → s_1)^w⟩, ⟨(s_2 → s_3 → s_0 → s_1)^* → s_2 → s_4⟩ T r a c e s ( s 2 ) = ⟨ s 2 → s 4 ⟩ , ⟨ ( s 2 → s 3 → s 0 → s 1 ) w ⟩ , ⟨ ( s 2 → s 3 → s 0 → s 1 ) ∗ → s 2 → s 4 ⟩ T r a c e s ( s 0 ) = ⟨ ( s 0 → s 1 → s 2 → s 3 ⟩ w , ⟨ s 0 → s 1 → ( s 2 → s 3 → s 0 → s 1 ) ∗ → s 2 → s 4 ⟩ Traces(s_0) = ⟨(s_0 → s_1 → s_2 → s_3⟩^w, ⟨s_0 → s_1 → (s_2 → s_3 → s_0 → s_1)^* → s_2 → s_4⟩ T r a c e s ( s 0 ) = ⟨ ( s 0 → s 1 → s 2 → s 3 ⟩ w , ⟨ s 0 → s 1 → ( s 2 → s 3 → s 0 → s 1 ) ∗ → s 2 → s 4 ⟩ E x e c ( S ) = T r a c e s ( s 0 ) Exec(S) = Traces(s_0) E x e c ( S ) = T r a c e s ( s 0 )
T r a c e s ( s 2 ) = ⟨ ( s 2 → s 3 ) w ⟩ , ⟨ ( s 2 → s 3 ) ∗ → s 2 → s 4 ⟩ Traces(s_2) = ⟨(s_2 → s_3)^w⟩, ⟨(s_2 → s_3)^* → s_2 → s_4⟩ T r a c e s ( s 2 ) = ⟨ ( s 2 → s 3 ) w ⟩ , ⟨ ( s 2 → s 3 ) ∗ → s 2 → s 4 ⟩ T r a c e s ( s 0 ) = ⟨ ( s 0 → ( s 2 → s 3 ) w ⟩ , ⟨ ( s 0 → ( s 2 → s 3 ) ∗ → s 2 → s 4 ⟩ Traces(s_0) = ⟨(s_0 → (s_2 → s_3)^w⟩, ⟨(s_0 → (s_2 → s_3)^* → s_2 → s_4⟩ T r a c e s ( s 0 ) = ⟨ ( s 0 → ( s 2 → s 3 ) w ⟩ , ⟨ ( s 0 → ( s 2 → s 3 ) ∗ → s 2 → s 4 ⟩ T r a c e s ( s 1 ) = ⟨ ( s 1 → ( s 3 → s 2 ) w ⟩ , ⟨ ( s 1 → ( s 3 → s 2 ) + → s 4 ⟩ Traces(s_1) = ⟨(s_1 → (s_3 → s_2)^w⟩, ⟨(s_1 → (s_3 → s_2)^+ → s_4⟩ T r a c e s ( s 1 ) = ⟨ ( s 1 → ( s 3 → s 2 ) w ⟩ , ⟨ ( s 1 → ( s 3 → s 2 ) + → s 4 ⟩ E x e c ( S ) = T r a c e s ( s 0 ) ∪ T r a c e s ( s 1 ) Exec(S) = Traces(s_0) \cup Traces(s_1) E x e c ( S ) = T r a c e s ( s 0 ) ∪ T r a c e s ( s 1 )
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩
s ∈ S s ∈ S s ∈ S s s s s s s A c c ( S ) Acc(S) A c c ( S ) S S S
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩
执行图是有向图,其中:
顶点集是 A c c ( S ) Acc(S) A c c ( S )
有向边的集合是 R R R
因此它是$ ⟨S ∩ Acc(S), R ∩ (Acc(S) × Acc(S))⟩ $ 的图。
被标记的变迁系统 是一个五元组⟨ S 、 I 、 R 、 L 、 E t i q ⟩ ⟨S、I、R、L、Etiq⟩ ⟨ S 、 I 、 R 、 L 、 E t i q ⟩
S S S I ⊆ S I ⊆ S I ⊆ S R ⊆ S × S R ⊆ S × S R ⊆ S × S L L L E t i q Etiq E t i q E t i q ∈ R → L Etiq ∈ R → L E t i q ∈ R → L
被标记的变迁系统 非常接近自动机。但是没有 terminal state + infinity execution。
被标记的变迁系统 ⟨ S , I , R , L , E t i q ⟩ ⟨S, I, R, L, Etiq⟩ ⟨ S , I , R , L , E t i q ⟩ 等价于 由如下定义的 未标记系统⟨ S ′ , I ′ , R ′ ⟩ ⟨S', I', R'⟩ ⟨ S ′ , I ′ , R ′ ⟩
S ′ = ( L ∪ { ϵ } ) × S S' = (L \cup \{ \epsilon \}) \times S S ′ = ( L ∪ { ϵ } ) × S I ′ = { ϵ } × I I' = \{ \epsilon \} \times I I ′ = { ϵ } × I R ′ = { ( ⟨ I , s ⟩ , ⟨ I ′ , s ′ ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ I ′ = E t i q ( s , s ′ ) } R' = \{ ( ⟨I,s⟩, ⟨I',s'⟩ )| (s, s') \in R \land I' = Etiq(s,s')\} R ′ = { ( ⟨ I , s ⟩ , ⟨ I ′ , s ′ ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ I ′ = E t i q ( s , s ′ ) }
转换(transition) $s_1 \xrightarrow{a} s_2 $ 可变成 $ ⟨_,s_1⟩ \to ⟨a,s_2⟩$,其中 _ 是任何标签。
可变为
转换没有标签:Pas d’étiquette sur les transitions (ou comme si)
转换不是由环境引起的:Une transition n’est pas causée par l’environnement
没有终结状态:Pas d’états terminaux
可能有许多的有限状态:Nombre d’états infini possible
可能有无限的执行:Exécution infinie possible
在执行图(Graphe d’exécution) 中显式地给出,例如以图像形式或通过顶点和边的集合。仅适用于状态和转换数量有限 的变迁系统。
基于变量的变迁系统的三元组$ ⟨V, Init,Trans⟩ $ 中,
V = { v 1 , . . . , v n } V = \{ v_1, ..., v_n\} V = { v 1 , . . . , v n } I n i t ( v 1 , . . . , v n ) Init(v_1, ..., v_n) I n i t ( v 1 , . . . , v n ) v i v_i v i T r a n s ( v 1 , . . . , v n , v 1 ′ , . . . , v n ′ ) Trans(v_1, ..., v_n, {v_1}', ..., {v_n}') T r a n s ( v 1 , . . . , v n , v 1 ′ , . . . , v n ′ ) v i v_i v i v i ′ {v_i}' v i ′
1 2 3 4 i = 0 ; while (i < N) { i = i+1 ; }
在显式的表示中,N = 5 N = 5 N = 5
⟨ ( 0 , 1 , 2 , 3 , 4 , 5 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) } ⟩ ⟨(0, 1, 2, 3, 4, 5), \{ 0\}, \{ (0,1), (1,2), (2,3), (3,4), (4,5)\}⟩
⟨ ( 0 , 1 , 2 , 3 , 4 , 5 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) } ⟩
执行图(Graphe d’exécution)为
0 → 1 → 2 → 3 → 4 → 5 0 \to 1 \to 2 \to 3 \to 4 \to5
0 → 1 → 2 → 3 → 4 → 5
隐式的表示为:
V ≜ i ∈ N V \triangleq i \in \mathbb{N} V ≜ i ∈ N I n i t ≜ i = 0 Init \triangleq i = 0 I n i t ≜ i = 0 T r a n s ≜ i < N ∧ i ′ = i + 1 Trans \triangleq i < N \land i' = i+1 T r a n s ≜ i < N ∧ i ′ = i + 1 T r a n s ≜ i ′ ≤ N ∧ i ′ − i = 1 Trans \triangleq i' \leq N \land i'-i=1 T r a n s ≜ i ′ ≤ N ∧ i ′ − i = 1
1 2 3 4 i = 0 ; while (true ) { i = (i+1 ) % N; }
在显式的表示中,N = 4 N = 4 N = 4
⟨ ( 0 , 1 , 2 , 3 , 4 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 0 ) } ⟩ ⟨(0, 1, 2, 3, 4), \{ 0\}, \{ (0,1), (1,2), (2,3), (3,4), (4,0)\}⟩
⟨ ( 0 , 1 , 2 , 3 , 4 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 0 ) } ⟩
执行图(Graphe d’exécution)为
隐式的表示为:
V ≜ i ∈ N V \triangleq i \in \mathbb{N} V ≜ i ∈ N I n i t ≜ i = 0 Init \triangleq i = 0 I n i t ≜ i = 0 $Trans \triangleq i’ = (i+1) \mod N $
1 2 3 4 5 6 i = 0 ; while (true ) { i > 0 -> i = i - 1 ; or i < N -> i = i + 1 ; }
在显式的表示中,N = 5 N = 5 N = 5
⟨ ( 0 , 1 , 2 , 3 , 4 , 5 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 5 , 4 ) , ( 4 , 3 ) , ( 3 , 2 ) , ( 2 , 1 ) } ⟩ ⟨(0, 1, 2, 3, 4, 5), \{ 0\}, \{ (0,1), (1,2), (2,3), (3,4), (4,5), (5,4), (4,3), (3,2), (2,1)\}⟩
⟨ ( 0 , 1 , 2 , 3 , 4 , 5 ) , { 0 } , { ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 5 , 4 ) , ( 4 , 3 ) , ( 3 , 2 ) , ( 2 , 1 ) } ⟩
执行图(Graphe d’exécution)为
隐式的表示为:
V ≜ i ∈ N V \triangleq i \in \mathbb{N} V ≜ i ∈ N I n i t ≜ i = 0 Init \triangleq i = 0 I n i t ≜ i = 0 $Trans \triangleq (i > 0 \land i’=i-1) \lor (i < N \land i’=i+1) $ 或 T r a n s ≜ ∣ i ′ − i ∣ = 1 ∧ 0 ≤ i ′ ≤ N Trans \triangleq \left| i' -i \right| = 1 \land 0 \leq i' \leq N T r a n s ≜ ∣ i ′ − i ∣ = 1 ∧ 0 ≤ i ′ ≤ N
对于符号描述⟨ V , I n i t , T r a n s ⟩ ⟨V, Init,Trans⟩ ⟨ V , I n i t , T r a n s ⟩ ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩
S = ∏ i ∈ 1.. n D i S = \prod_{i \in 1..n} D_i S = ∏ i ∈ 1 . . n D i D 1 , . . . , D n D_1,...,D_n D 1 , . . . , D n v 1 , . . . , v n v_1, ..., v_n v 1 , . . . , v n I = { ( v 1 , . . . , v n ) ∣ I n i t ( v 1 , . . . , v n ) } I = \{ (v_1,...,v_n) | Init(v_1, ..., v_n)\} I = { ( v 1 , . . . , v n ) ∣ I n i t ( v 1 , . . . , v n ) } R = { ( ( v 1 , . . . , v n ) , ( v 1 ′ , . . . , v n ′ ) ) ∣ T r a n s ( v 1 , . . . , v n , v 1 ′ , . . . , v n ′ ) } R = \{ ((v_1, ..., v_n),({v_1}', ..., {v_n}')) | Trans(v_1, ..., v_n,{v_1}', ..., {v_n}')\} R = { ( ( v 1 , . . . , v n ) , ( v 1 ′ , . . . , v n ′ ) ) ∣ T r a n s ( v 1 , . . . , v n , v 1 ′ , . . . , v n ′ ) }
状态谓词是与隐式表示的系统的(状态)变量有关的谓词。
状态谓词可以看作是 S 的一部分的特征函数。
转换谓词是与已启动和未启动(状态)变量相关的谓词。
转换谓词可以看作是 S × S S × S S × S
$V \triangleq n \in \mathbb{N} $
I n i t ≜ − 5 ≤ n ≤ 5 Init \triangleq -5 \leq n \leq 5 I n i t ≜ − 5 ≤ n ≤ 5
T r a n s ≜ n ≠ 1 ∧ ( ( n ′ = n / 2 ∧ n ≡ 0 [ 2 ] ) ∨ ( n ′ = ( 3 n + 1 ) / 2 ∧ n ≡ 1 [ 2 ] ) ) Trans \triangleq n \neq 1 \land ((n' = n/2 \land n \equiv 0[2]) \lor (n' = (3n+1)/2 \land n \equiv 1[2])) T r a n s ≜ n = 1 ∧ ( ( n ′ = n / 2 ∧ n ≡ 0 [ 2 ] ) ∨ ( n ′ = ( 3 n + 1 ) / 2 ∧ n ≡ 1 [ 2 ] ) )
Prédicat d’état : $ Init, n < 20 $
Prédicat de transition : T r a n s , n ′ − n > 3 Trans, n' − n > 3 T r a n s , n ′ − n > 3
一个系统有一个死锁 ≜ \triangleq ≜
对于建模经典顺序程序的系统,死锁相当于终止。
一个系统可以从任何可访问的状态重置 ≜ \triangleq ≜
这个属性意味着在任何时候,都有一系列的转换(transitions)返回到系统的初始状态,从而重新启动。 这样的系统只有无限的执行。
重复状态 ≜ \triangleq ≜ ( s , s ) ∈ R (s,s) ∈ R ( s , s ) ∈ R
一个重复变迁系统 ≜ \triangleq ≜ I d ⊆ R Id ⊆ R I d ⊆ R
用处
我们可以在 s 0 s_0 s 0 s 1 s_1 s 1
无限的执行:在无重复系统中,任何没有后继者的状态都有一个独特的后继者:它自己。
终止状态时(或死锁). . . → s i ... \to s_i . . . → s i . . . → s i w ... \to {s_i}^w . . . → s i w
可以组成几个变迁系统。
变迁系统 ⟨ V , I , T ⟩ ⟨V,I,T⟩ ⟨ V , I , T ⟩ ⟨ V 1 , I 1 , T 1 ⟩ ⟨V_1, I_1,T_1⟩ ⟨ V 1 , I 1 , T 1 ⟩
V ≜ V 1 ∪ V 2 V \triangleq V_1 \cup V_2 V ≜ V 1 ∪ V 2 V 1 V_1 V 1 V 2 V_2 V 2 I ≜ I 1 ∧ I 2 I \triangleq I_1 \land I_2 I ≜ I 1 ∧ I 2 $ T \triangleq T_1 ∧ T_2 $ :每个子系统都根据其转换(transition)演变
由于 T 1 T_1 T 1 T 2 T_2 T 2 T 1 ∧ T 2 T_1 ∧ T_2 T 1 ∧ T 2 T 1 T_1 T 1 T 2 T_2 T 2 T 2 T_2 T 2 T 1 T_1 T 1
例:
( V 1 ≜ i ∈ N I 1 ≜ i = 0 T 1 ≜ { i ′ = i + 1 ∨ i ′ = i ) ⊗ ( V 2 ≜ j ∈ N I 2 ≜ j = 0 T 2 ≜ { j ′ = j + 1 ∨ j ′ = j ) → ( V ≜ i , j ∈ N I ≜ i = 0 ∧ j = 0 T ≜ { i ′ = i + 1 ∧ j ′ = j ∨ ( i ′ = i ∧ j ′ = j + 1 ) ∨ ( i ′ = i + 1 ∧ j ′ = j + 1 ) ∨ ( i ′ = i ∧ j ′ = j ) ) \left(
\begin{matrix}
V_1 \triangleq i \in \mathbb{N}\\
I_1 \triangleq i = 0 \\
T_1 \triangleq
\begin{cases}
i'=i+1\\
\lor \ i'=i\\
\end{cases}\\
\end{matrix}
\right)
\otimes
\left(
\begin{matrix}
V_2 \triangleq j \in \mathbb{N}\\
I_2 \triangleq j = 0 \\
T_2 \triangleq
\begin{cases}
j'=j+1\\
\lor \ j'=j\\
\end{cases}\\
\end{matrix}
\right)
\to
\left(
\begin{matrix}
V \triangleq i,j \in \mathbb{N}\\
I \triangleq i=0 \land j=0\\
T \triangleq
\begin{cases}
i'=i+1 \land j' = j\\
\lor \ (i'=i \land j'=j+1)\\
\lor \ (i'=i+1 \land j'=j+1)\\
\lor \ (i'=i \land j'=j)
\end{cases}\\
\end{matrix}
\right)
⎝ ⎜ ⎜ ⎜ ⎛ V 1 ≜ i ∈ N I 1 ≜ i = 0 T 1 ≜ { i ′ = i + 1 ∨ i ′ = i ⎠ ⎟ ⎟ ⎟ ⎞ ⊗ ⎝ ⎜ ⎜ ⎜ ⎛ V 2 ≜ j ∈ N I 2 ≜ j = 0 T 2 ≜ { j ′ = j + 1 ∨ j ′ = j ⎠ ⎟ ⎟ ⎟ ⎞ → ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ V ≜ i , j ∈ N I ≜ i = 0 ∧ j = 0 T ≜ ⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ i ′ = i + 1 ∧ j ′ = j ∨ ( i ′ = i ∧ j ′ = j + 1 ) ∨ ( i ′ = i + 1 ∧ j ′ = j + 1 ) ∨ ( i ′ = i ∧ j ′ = j ) ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
变迁系统 ⟨ S , I , R , L ⟩ ⟨S,I,R,L⟩ ⟨ S , I , R , L ⟩ ⟨ S 1 , I 1 , R 1 , L 1 ⟩ ⟨S_1,I_1,R_1,L_1⟩ ⟨ S 1 , I 1 , R 1 , L 1 ⟩ ⟨ S 2 , I 2 , R 2 , L 2 ⟩ ⟨S_2,I_2,R_2,L_2⟩ ⟨ S 2 , I 2 , R 2 , L 2 ⟩
S ≜ S 1 × S 2 S \triangleq S_1 \times S_2 S ≜ S 1 × S 2 I ≜ I 1 × I 2 I \triangleq I_1 \times I_2 I ≜ I 1 × I 2 R ≜ { ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ′ ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 1 , s 1 ′ ) ) = E t i q ( ( s 2 , s 2 ′ ) ) } R \triangleq \{ ((s_1, s_2), ({s_1}', {s_2}')) | (s_1, {s_1}') \in R_1 \land (s_2, {s_2}') \in R_2 \land Etiq((s_1, {s_1}')) = Etiq((s_2, {s_2}')) \} R ≜ { ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ′ ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 1 , s 1 ′ ) ) = E t i q ( ( s 2 , s 2 ′ ) ) } $ L \triangleq L_1 \cap L_2 $
例:
Synchronizé strict avec LIFO 2 éléments (pile)
Donne:
Synchronizé strict avec FIFO 2 éléments (file)
Donne:
变迁系统 ⟨ S , I , R , L ⟩ ⟨S,I,R,L⟩ ⟨ S , I , R , L ⟩ ⟨ S 1 , I 1 , R 1 , L 1 ⟩ ⟨S_1,I_1,R_1,L_1⟩ ⟨ S 1 , I 1 , R 1 , L 1 ⟩ ⟨ S 2 , I 2 , R 2 , L 2 ⟩ ⟨S_2,I_2,R_2,L_2⟩ ⟨ S 2 , I 2 , R 2 , L 2 ⟩
S ≜ S 1 × S 2 S \triangleq S_1 \times S_2 S ≜ S 1 × S 2
I ≜ I 1 × I 2 I \triangleq I_1 \times I_2 I ≜ I 1 × I 2
R ≜ { ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ′ ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 1 , s 1 ′ ) ) = E t i q ( ( s 2 , s 2 ′ ) ) ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ E t i q ( ( s 1 , s 1 ′ ) ) ∉ L 2 ( ( s 1 , s 2 ) , ( s 1 , s 2 ′ ) ) ∣ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 2 , s 2 ′ ) ) ∉ L 1 R \triangleq
\begin{cases}
((s_1, s_2), ({s_1}', {s_2}')) | (s_1, {s_1}') \in R_1 \land (s_2, {s_2}') \in R_2 \land Etiq((s_1, {s_1}')) = Etiq((s_2, {s_2}'))\\
((s_1, s_2), ({s_1}', {s_2})) | (s_1, {s_1}') \in R_1 \land Etiq((s_1, {s_1}')) \notin L_2\\
((s_1, s_2), ({s_1}, {s_2}')) | (s_2, {s_2}') \in R_2 \land Etiq((s_2, {s_2}')) \notin L_1
\end{cases}
R ≜ ⎩ ⎪ ⎨ ⎪ ⎧ ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ′ ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 1 , s 1 ′ ) ) = E t i q ( ( s 2 , s 2 ′ ) ) ( ( s 1 , s 2 ) , ( s 1 ′ , s 2 ) ) ∣ ( s 1 , s 1 ′ ) ∈ R 1 ∧ E t i q ( ( s 1 , s 1 ′ ) ) ∈ / L 2 ( ( s 1 , s 2 ) , ( s 1 , s 2 ′ ) ) ∣ ( s 2 , s 2 ′ ) ∈ R 2 ∧ E t i q ( ( s 2 , s 2 ′ ) ) ∈ / L 1
$ L \triangleq L_1 \cap L_2 $
例:
Synchronizé strict avec LIFO 2 éléments (pile)
Donne:
ouvert
在《概述》中,我们提到T emporal L ogic of A ctions +是由Leslie Lamport 开发的一种 【形式化验证语言】 。
本章我们会简单介绍这种语言。
一个TLA+的Model里应该包含的元素有:
常数 Constant
变量 Variable(状态 = 变量的值)
Init. State 由状态谓词定义的一组初始状态
动作 Action = 连接两个状态的转换谓词:
当前状态,未启动的变量
到达状态,主要变量
由动作的析取构造的过渡谓词(≈无限重复动作)
例:
1 2 3 4 5 6 7 8 9 10 11 12 ---------------- MODULE example ---------------- EXTENDS Naturals VARIABLE x \* 初始状态 Init是初始化谓词(initial predicate) Init == x \in 0..2 \* 等价于x属于自然数 并且 0 <= x < 3 \* 动作 Plus == x'=x+1 Sub == x>0 /\ x'=x-1 Next == Plus \/ Sub \* Next是Next-state动作(action) Spec == Init /\ [] [ Next ]_<<x>>
上述规约语言等价于下述变迁系统
V ≜ x ∈ N V \triangleq x \in \mathbb{N} V ≜ x ∈ N I ≜ 0 ≤ x ≤ 2 I \triangleq 0 \le x \le 2 I ≜ 0 ≤ x ≤ 2 R ≜ { x ′ = x + 1 ∨ x > 0 ∧ x ′ = x − 1 ∨ x ′ = x R \triangleq \begin{cases} x' = x+1\\ \lor x>0 \land x'=x-1\\ \lor x'=x \end{cases} R ≜ ⎩ ⎪ ⎨ ⎪ ⎧ x ′ = x + 1 ∨ x > 0 ∧ x ′ = x − 1 ∨ x ′ = x
显式常量:0、1、true、false、“string”
命名常量:C O N S T A N T N _{CONSTANT} \ N C O N S T A N T N A S S U M E N ∈ N a t ∧ N ≥ 2 _{ASSUME}\ N \in Nat \land N \ge 2 A S S U M E N ∈ N a t ∧ N ≥ 2
一切可以公理化的东西:
逻辑表达式:¬ , ∧ , ∨ , ∀ x ∈ S : p ( x ) , ∃ x ∈ S : p ( x ) ¬, ∧, ∨, ∀x ∈ S:p(x), ∃x ∈ S:p(x) ¬ , ∧ , ∨ , ∀ x ∈ S : p ( x ) , ∃ x ∈ S : p ( x )
算术表达式:+ , − , > , . . . +,-,>,... + , − , > , . . .
集合表达式: ∈ ∈ ∈ ∪ ∪ ∪ ∩ ∩ ∩ ⊂ ⊂ ⊂ { e 1 , e 2 , . . . , e n } \{e1, e2, . . . , en\} { e 1 , e 2 , . . . , e n } n . . m n..m n . . m { x ∈ S : p ( x ) } \{x ∈ S : p(x)\} { x ∈ S : p ( x ) } { f ( x ) : x ∈ S } \{f (x) : x ∈ S\} { f ( x ) : x ∈ S } U N I O N S _{UNION}\ S U N I O N S S U B S E T S _{SUBSET} \ S S U B S E T S
I F _{IF} I F T H E N _{THEN} T H E N E L S E _{ELSE} E L S E 从 X 到 Y 的函数
元组、序列等
{ e 1 , . . . , e n } \{e_1, ...,e_n\} { e 1 , . . . , e n } n . . m n ..m n . . m i ∈ N a t : n ≤ i ≤ m i \in Nat : n \le i \le m i ∈ N a t : n ≤ i ≤ m { x ∈ S : p ( x ) } \{ x \in S : p(x)\} { x ∈ S : p ( x ) }
例1,${ n \in 1…10 : n%2=0} = {2,4,6,8,10} $
例2,${ n \in Nat : n%2=1} = {所有的奇数} $
${ f(x) :x \in S} $ :所有f ( x ) f(x) f ( x )
例1,${ 2*n: n \in 1…5} = {2,4,6,8,10} $
例2,${2*n+1 : n \in Nat} = {所有的奇数} $
U N I O N S _{UNION}\ S U N I O N S
U N I O N { { 1 , 2 } , { 3 , 4 } } = { 1 , 2 , 3 , 4 } _{UNION} \{ \{ 1,2\}, \{ 3,4\}\} = \{ 1,2,3,4\} U N I O N { { 1 , 2 } , { 3 , 4 } } = { 1 , 2 , 3 , 4 }
S U B S E T S _{SUBSET}\ S S U B S E T S
S U B S E T { 1 , 2 } = { { } , { 1 } , { 2 } , { 1 , 2 } } _{SUBSET} \{ 1,2\} = \{ \{\}, \{1\}, \{ 2\}, \{ 1,2\}\} S U B S E T { 1 , 2 } = { { } , { 1 } , { 2 } , { 1 , 2 } }
e ′ e' e ′ [ A ] e [A]_e [ A ] e [ A ∨ ( e ′ = e ) ] [A ∨ (e' = e)] [ A ∨ ( e ′ = e ) ] ⟨ A ⟩ e ⟨A⟩_e ⟨ A ⟩ e [ A ∧ ( e ′ ≠ e ) ] [A ∧ (e' \ne e)] [ A ∧ ( e ′ = e ) ] E N A B L E A _{ENABLE} \ A E N A B L E A U N C H A N G E D E _{UNCHANGED}\ E U N C H A N G E D E [ e ′ = e ] [e' = e] [ e ′ = e ] A ⋅ B A · B A ⋅ B
动作 = 转换谓词 = 包含常量、变量和引发变量的布尔表达式。
动作 不等于 任务
仅与起始状态有关的状态谓词
确定性转移谓词 v a r ′ = . . . var' = . . . v a r ′ = . . . v a r ′ ∈ . . . var' ∈ ... v a r ′ ∈ . . .
例:x < 10 ∧ x ′ = x + 1 x < 10 ∧ x' = x + 1 x < 1 0 ∧ x ′ = x + 1 x ′ = x + 1 ∧ x ′ < 11 x′ = x + 1 ∧ x' < 11 x ′ = x + 1 ∧ x ′ < 1 1 x ′ − x = 1 ∧ x ′ < 11 x′ - x = 1 ∧ x' < 11 x ′ − x = 1 ∧ x ′ < 1 1
[ A ] f ≜ A ∨ f ′ = f [\mathcal{A}]_f \triangleq \mathcal{A} ∨ f' = f [ A ] f ≜ A ∨ f ′ = f f f f
示例:
[ x ′ = x + 1 ] ⟨ x , y ⟩ = ( x ′ = x + 1 ∨ ( ⟨ x , y ⟩ ′ = ⟨ x , y ⟩ ) ) = ( x ′ = x + 1 ∨ ( x ′ = x ∧ y ′ = y ) ) \begin{aligned} {[x'=x+1]_{⟨x,y⟩}} & = {(x'=x+1 ∨ (⟨x, y⟩'=⟨x,y⟩))} \\ & = {(x'= x+1 ∨ (x'=x ∧ y'=y))} \\ \end{aligned} [ x ′ = x + 1 ] ⟨ x , y ⟩ = ( x ′ = x + 1 ∨ ( ⟨ x , y ⟩ ′ = ⟨ x , y ⟩ ) ) = ( x ′ = x + 1 ∨ ( x ′ = x ∧ y ′ = y ) )
[ A ] f ≜ A ∨ f ′ ≠ f [\mathcal{A}]_f \triangleq \mathcal{A} ∨ f' \ne f [ A ] f ≜ A ∨ f ′ = f f f f
( x ′ = x + 1 ) = ( x ′ = x + 1 ∧ y ′ = 任 何 值 ) ≠ ( x ′ = x + 1 ∧ y ′ = y ) \begin{aligned} {(x′=x+1)} & = {(x'=x+1 \land y'= 任何值 )} \\ & \ne {(x'=x+1 \land y'=y)} \\ \end{aligned} ( x ′ = x + 1 ) = ( x ′ = x + 1 ∧ y ′ = 任 何 值 ) = ( x ′ = x + 1 ∧ y ′ = y )
U N C H A N G E D e ≜ e ′ = e _{UNCHANGED}\ e \triangleq e' = e U N C H A N G E D e ≜ e ′ = e
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 ---------------- MODULE AlternatingBit ---------------- EXTENDS Naturals CONSTANT Data VARIABLE val, ready, ack ------------------------------------------------------- \* 初始状态 Init是初始化谓词(initial predicate) Init == /\ val \in Data /\ ready \in {0,1} /\ ack = ready Send == /\ ready = ack /\ val' \in Data /\ ready' = 1 - ready /\ UNCHANGED ack Receive == /\ ready # ac k /\ ack' = 1 - ack /\ UNCHANGED <<val, ready>> ------------------------------------------------------- Next == Send \/ Receive \* Next是Next-state动作(action) Spec == Init /\ [] [ Next ]_<<val, ready, ack>> =========================================================
“映射(mapping) ”意义上的函数,对应:
X → Y X \to Y X → Y f ∈ [ X → Y ] f \in [X \to Y] f ∈ [ X → Y ] f [ x ] f[x] f [ x ]
一个函数就是一个值。
f [ x ∈ N a t ] f[x \in Nat] f [ x ∈ N a t ] I n c [ x ∈ N a t ] ≜ x + 1 Inc[x \in Nat] \triangleq x+1 I n c [ x ∈ N a t ] ≜ x + 1
[ x ∈ S ↦ e x p r ] [x \in S \mapsto expr] [ x ∈ S ↦ e x p r ] x ∈ 1..4 ↦ 2 ∗ x x \in 1..4 \mapsto 2*x x ∈ 1 . . 4 ↦ 2 ∗ x
函数 t ∈ [ X → Y ] t ∈ [X → Y ] t ∈ [ X → Y ]
D O M A I N f _{DOMAIN}\ f D O M A I N f
C o d o m a i n ( f ) ≜ { f [ x ] : x ∈ D O M A I N f } Codomain(f) \triangleq \{ f[x]:x \in _{DOMAIN}f\} C o d o m a i n ( f ) ≜ { f [ x ] : x ∈ D O M A I N f }
[ a E X C E P T ! [ i ] = v ] ≜ [ j ∈ D O M A I N a ↦ I F j = i T H E N v E L S E a [ j ] ] [a \ _{EXCEPT}\ ![i] =v] \triangleq [j\in _{DOMAIN} \ a \mapsto _{IF}\ j=i\ _{THEN}\ v\ _{ELSE}\ a[j]] [ a E X C E P T ! [ i ] = v ] ≜ [ j ∈ D O M A I N a ↦ I F j = i T H E N v E L S E a [ j ] ]
例:[ a ′ = a E X C E P T ! [ 2 ] = 8 ] ≢ ( a [ 2 ] ′ = 8 ) [a' = a \ _{EXCEPT}\ ![2] =8] \not\equiv (a[2]' =8) [ a ′ = a E X C E P T ! [ 2 ] = 8 ] ≡ ( a [ 2 ] ′ = 8 )
IncF 是数学意义上的函数定义,等价于 I n c F ≜ [ x ∈ N a t ↦ x + 1 ] IncF \triangleq [x ∈ Nat \mapsto x + 1] I n c F ≜ [ x ∈ N a t ↦ x + 1 ]
它的定义域:D O M A I N I n c F _{DOMAIN}\ IncF D O M A I N I n c F
它的值域:$ {IncF[x] : x ∈ _{DOMAIN}IncF}$
I n c F ∈ [ X ↦ Y ] IncF \in [X \mapsto Y] I n c F ∈ [ X ↦ Y ]
IncO 是运算符(Operator) 的定义
写因式分解:类似于一个宏,其文本可以替换
没有定义域 和 值域
I n c O ∈ [ X → Y ] IncO ∈ [X → Y ] I n c O ∈ [ X → Y ]
记录是 [ X → Y ] [X → Y] [ X → Y ]
简写作:[ " q w e r t y " ↦ 1 , " a s d f g h " ↦ 2 ] = [ q w e r t y ↦ 1 , a s d f g h ↦ 2 ] ["qwerty" \mapsto 1, "asdfgh" \mapsto 2] = [qwerty \mapsto 1,asdfgh \mapsto 2] [ " q w e r t y " ↦ 1 , " a s d f g h " ↦ 2 ] = [ q w e r t y ↦ 1 , a s d f g h ↦ 2 ]
r e c [ " q w e r t y " ] = r e c . q w e r t y rec["qwerty"] = rec.qwerty r e c [ " q w e r t y " ] = r e c . q w e r t y
定义(函数或运算符)时,可以给出递归定义:
函数:f a c t [ n ∈ N a t ] ≜ I F n = 0 T H E N 1 E L S E n ∗ f a c t ( n − 1 ) fact[n \in Nat] \triangleq _{IF}\ n=0\ _{THEN}\ 1\ _{ELSE}\ n*fact(n-1) f a c t [ n ∈ N a t ] ≜ I F n = 0 T H E N 1 E L S E n ∗ f a c t ( n − 1 )
运算符:f a c t ( n ) ≜ I F n = 0 T H E N 1 E L S E n ∗ f a c t ( n − 1 ) fact(n) \triangleq _{IF}\ n=0\ _{THEN}\ 1\ _{ELSE}\ n*fact(n-1) f a c t ( n ) ≜ I F n = 0 T H E N 1 E L S E n ∗ f a c t ( n − 1 )
从理论上讲,必须证明这些定义的有效性。
符号:⟨a, b, c⟩。
n元组是定义域函数= { 1 , . . . , n } : ⟨ a , b , c ⟩ [ 3 ] = c \{1,. . .,n\} :⟨a, b, c⟩[3] = c { 1 , . . . , n } : ⟨ a , b , c ⟩ [ 3 ] = c
用于表示关系:{ ⟨ x , y ⟩ ∈ X × Y : R ( x , y ) } \{⟨x, y⟩ ∈ X × Y: R(x, y)\} { ⟨ x , y ⟩ ∈ X × Y : R ( x , y ) } { ⟨ a , b ⟩ ∈ N a t × N a t : a = 2 ∗ b } \{⟨a, b⟩ ∈ Nat × Nat:a=2*b\} { ⟨ a , b ⟩ ∈ N a t × N a t : a = 2 ∗ b }
S e q ( T ) ≜ U N I O N { [ 1.. n → T ] : n ∈ N a t } ≜ 包 含 T 的 有 限 序 列 集 \begin{aligned} Seq(T) & \triangleq _{UNION} \{[1..n → T]: n ∈ Nat\}\\ & \triangleq 包含 T 的有限序列集 \end{aligned} S e q ( T ) ≜ U N I O N { [ 1 . . n → T ] : n ∈ N a t } ≜ 包 含 T 的 有 限 序 列 集
运算符:L e n ( s ) Len(s) L e n ( s ) s ◦ t s ◦ t s ◦ t A p p e n d ( s , e ) Append(s,e) A p p e n d ( s , e ) H e a d ( s ) Head(s) H e a d ( s ) T a i l ( s ) Tail(s) T a i l ( s )
L E T LET L E T
表达式: L E T v ≜ e I N f _{LET}\ v \triangleq e\ _{IN}\ f L E T v ≜ e I N f
等效于表达式 f f f v v v e e e L E T i ≜ g ( x ) I N f ( i ) ≡ f ( g ( x ) ) _{LET}\ i \triangleq g(x)\ _{IN}\ f (i)≡ f (g(x)) L E T i ≜ g ( x ) I N f ( i ) ≡ f ( g ( x ) )
例:
P y t h a g o r e ( x , y , z ) ≜ L E T s q u a r e ( n ) ≜ n ∗ n I N s q u a r e ( x ) + s q u a r e ( y ) = s q u a r e ( z ) Pythagore(x, y, z) \triangleq _{LET}\ square(n) \triangleq n∗n\ _{IN}\ square(x) + square(y) = square(z) P y t h a g o r e ( x , y , z ) ≜ L E T s q u a r e ( n ) ≜ n ∗ n I N s q u a r e ( x ) + s q u a r e ( y ) = s q u a r e ( z )
C H O O S E x ∈ S : p _{CHOOSE}\ x \in S:p C H O O S E x ∈ S : p
m a x [ S ∈ S U B S E T N a t ] ≜ C H O O S E m ∈ S : ( ∀ p ∈ S : m ≥ p ) max[S \in _{SUBSET}\ Nat] \triangleq\ _{CHOOSE}\ m \in S:(\forall p \in S : m \ge p) m a x [ S ∈ S U B S E T N a t ] ≜ C H O O S E m ∈ S : ( ∀ p ∈ S : m ≥ p )
对于集合 S 和属性 p,选择的元素在所有执行过程中始终相同。 它不是一个随机选择器,它在每次调用时都给出一个不同的元素。所以C H O O S E x ∈ S : p = C H O O S E x ∈ S : p _{CHOOSE}\ x \in S:p = _{CHOOSE}\ x \in S:p C H O O S E x ∈ S : p = C H O O S E x ∈ S : p
规约
( x = C H O O S E n : n ∈ N a t ) ∧ □ [ x ′ = C H O O S E n : n ∈ N a t ] ⟨ x ⟩ (x =\ _{CHOOSE}\ n : n ∈ Nat) ∧ \Box [x'=_{CHOOSE}\ n : n ∈ Nat]_{⟨x⟩} ( x = C H O O S E n : n ∈ N a t ) ∧ □ [ x ′ = C H O O S E n : n ∈ N a t ] ⟨ x ⟩
有一个独特的执行:$ x = c → x = c → …$其中 c 是一个不确定的整数(由选择指定)。
( x ∈ N a t ) ∧ □ [ x ′ ∈ N a t ] ⟨ x ⟩ (x ∈ Nat) ∧ \Box [x' ∈ Nat]_{⟨x⟩} ( x ∈ N a t ) ∧ □ [ x ′ ∈ N a t ] ⟨ x ⟩
有无限次执行,其中一些在每个状态中 x 是不同的,另一些在 x 是恒定的,另一些在 x 中循环
因为线性时间属性(LT Properties)是TS中迹的要求,所以在原子命题(AP)上的线性时间属性是S w S^{w} S w S w S^{w} S w
如果AP={a,b},那么( 2 A P ) w (2^{AP})^{w} ( 2 A P ) w
{ { a } { a , b } ∅ . . . , { b } { a } ∅ ∅ . . . , . . . } \{\{a\}\{a,b\}\varnothing ...,\{b\}\{a\}\varnothing\varnothing...,...\}
{ { a } { a , b } ∅ . . . , { b } { a } ∅ ∅ . . . , . . . }
类似该集合中的元素,由无限个字符级联在一起组成的序列称为无限字(infinite word),无限字可以表示为:
W = A 0 A 1 A 2 . . . W=A_{0}A_{1}A_{2}...
W = A 0 A 1 A 2 . . .
当这个序列是有限时,便称为有限字(finite word),有限字可以表示为:
W = A 0 A 1 A 2 . . . A n W=A_{0}A_{1}A_{2}...A_{n}
W = A 0 A 1 A 2 . . . A n
因为TS不考虑终止状态,所以也就无需使用有限字。
如果一个TS满足线性时间属性P,那么就表明:
T S ⊨ P 当且仅当 T r a c e s ( T S ) ⊆ P TS \vDash P\text{ 当且仅当}Traces(TS) ⊆ P
T S ⊨ P 当且仅当 T r a c e s ( T S ) ⊆ P
我个人的理解是线性时间属性P刻画了AP上能够出现的原子命题序列,而迹表示的是系统在AP上出现的原子命题序列,如果系统的迹是P的子集,那么肯定这个系统就满足了线性时间属性P。
一说到信号量和互斥,再次搬出这个例子:
在这里,A P = { c r i t 1 , c r i t 2 } AP=\{crit_1, crit_2\} A P = { c r i t 1 , c r i t 2 }
“Always at most one process is in its critical section”
就是最多有一个进程能够进入临界区
用形式化的语言描述就是:
P m u t e x = 一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 且 满 足 对 于 所 有 0 ≤ i , { c r i t 1 , c r i t 2 } ⊈ A i P_{mutex} = 一个无限字的集合\{A_0A_1A_2...\} 且满足对于所有0\le i,\{crit_1, crit_2\} \nsubseteq A_{i}
P m u t e x = 一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 且 满 足 对 于 所 有 0 ≤ i , { c r i t 1 , c r i t 2 } ⊈ A i
这就完成对系统属性的刻画,描述一下就是对于这个TS的运行轨迹来说不存在{ c r i t 1 , c r i t 2 } \{crit_1, crit2\} { c r i t 1 , c r i t 2 }
所以无限字可以是类似{ c r i t 1 } { c r i t 2 } { c r i t 1 } { c r i t 2 } … \{crit_1\}\{crit_2\}\{crit_1\}\{crit_2\}… { c r i t 1 } { c r i t 2 } { c r i t 1 } { c r i t 2 } … ∅ ∅ ∅ ∅ ∅ … \varnothing\varnothing\varnothing\varnothing\varnothing… ∅ ∅ ∅ ∅ ∅ … { c r i t 1 , c r i t 2 } \{crit_1, crit2\} { c r i t 1 , c r i t 2 }
那么再问一个问题,上面的那个TS系统满足这个P m u t e x P_{mutex} P m u t e x
Yes,因为从图上看不存在{ c r i t 1 , c r i t 2 } \{crit_1, crit2\} { c r i t 1 , c r i t 2 }
不存在饥饿的系统要求满足条件:
“A process that wants to enter the critical section is eventually able to do so”
如果一个进程想要进入临界区,那么它最终总是能够进入临界区。
这一次让A P = { c r i t 1 , w a i t 1 , c r i t 2 , w a i t 2 } AP=\{crit_1,wait_1,crit_2,wait_2\} A P = { c r i t 1 , w a i t 1 , c r i t 2 , w a i t 2 }
用形式化的语言描述为LT性质就是:
P n o s t a r v e = 一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 满 足 ( ∃ ∞ j . w a i t i ∈ A j ) ⇒ ( ∃ ∞ j . c r i t i ∈ A j ) f o r e a c h i ∈ { 1 , 2 } P_{nostarve} = 一个无限字的集合\{A_0A_1A_2...\} \\ 满足(\overset{\infty}∃ j.\;wait_{i}∈A_{j})\Rightarrow (\overset{\infty}∃ j.\;crit_{i}∈A_{j})\; for\;each\;i∈\{1,2\}
P n o s t a r v e = 一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 满 足 ( ∃ ∞ j . w a i t i ∈ A j ) ⇒ ( ∃ ∞ j . c r i t i ∈ A j ) f o r e a c h i ∈ { 1 , 2 }
其中 ∃ ∞ \overset{\infty}∃ ∃ ∞
描述一下就是当一个进程进入等待状态后,之后肯定会进入临界区
那么基于信号量的互斥系统满足无饥饿性质嘛?no,如果是这样一条迹:∅ { w a i t 2 } { w a i t 1 , w a i t 2 } { c r i t 1 , w a i t 2 } { w a i t 2 } { w a i t 1 , w a i t 2 } { c r i t 1 , w a i t 2 } . . . \varnothing\{wait_2\}\{wait_1,wait_2\}\{crit_1,wait_2\}\{wait_2\}\{wait_1,wait_2\}\{crit_1,wait_2\}... ∅ { w a i t 2 } { w a i t 1 , w a i t 2 } { c r i t 1 , w a i t 2 } { w a i t 2 } { w a i t 1 , w a i t 2 } { c r i t 1 , w a i t 2 } . . .
事实上,上述(互斥与无死锁)安全性是一种特殊的性质:不变性。不变性是LT属性,由状态的条件Φ Φ Φ Φ Φ Φ
如果在AP上的线性属性P i n v P_{inv} P i n v
P i n v = { A 0 A 1 A 2 . . . ∈ ( 2 A P ) w ∣ ∀ j ≥ 0. A j ⊨ Φ } P_{inv}=\{A_{0}A_{1}A_{2}... ∈ (2^{AP})^{w} | ∀j \ge 0. A_{j} \vDash Φ \}
P i n v = { A 0 A 1 A 2 . . . ∈ ( 2 A P ) w ∣ ∀ j ≥ 0 . A j ⊨ Φ }
其中Φ Φ Φ Φ Φ Φ P i n v P_{inv} P i n v
让我们回想一下先前的基于信号量的互斥系统,在那个系统中Φ = ¬ c r i t 1 ∨ ¬ c r i t 2 Φ=\lnot crit1\vee \lnot crit2 Φ = ¬ c r i t 1 ∨ ¬ c r i t 2
I n v a r i a n t s ≜ ∀ c r i t 1 , c r i t 2 V a l u e : C h o s e n ( c r i t 1 ) ∧ C h o s e n ( c r i t 2 ) ⇒ c r i t 1 = c r i t 2 Invariants \triangleq \forall crit_1,crit_2 \; Value:Chosen(crit_1) \land Chosen(crit_2) \quad \Rightarrow \quad crit_1 = crit_2
I n v a r i a n t s ≜ ∀ c r i t 1 , c r i t 2 V a l u e : C h o s e n ( c r i t 1 ) ∧ C h o s e n ( c r i t 2 ) ⇒ c r i t 1 = c r i t 2
设TS是一个没有终止状态的转换系统,那么有:
T S ⊨ P i n v TS\vDash P_{inv} T S ⊨ P i n v
i f f t r a c e ( π ) ∈ P i n v f o r a l l p a t h s π i n T S iff\; trace(\pi)∈ P_{inv}\; for\; all\; paths\;\pi \; in\; TS i f f t r a c e ( π ) ∈ P i n v f o r a l l p a t h s π i n T S i f f L ( s ) ⊨ Φ f o r a l l s t a t e s s t h a t b e l o n g t o a p a t h o f T S iff\; L(s)\vDash Φ\; for\; all\; states\;s\;that\;belong\; to\; a\;path\; of\;TS i f f L ( s ) ⊨ Φ f o r a l l s t a t e s s t h a t b e l o n g t o a p a t h o f T S i f f L ( s ) ⊨ Φ f o r a l l s t a t e s s ∈ R e a c h ( T S ) iff\; L(s)\vDash Φ\; for\; all\; states\;s∈Reach(TS) i f f L ( s ) ⊨ Φ f o r a l l s t a t e s s ∈ R e a c h ( T S )
注意上面的最后一个式子,我们将TS能否满足不变性,转换成为了所有可达状态是否满足不变性这一问题。基于此我们可以设计检验不变性的算法。
我们只要遍历系统的每个状态,从初始状态开始,利用深度优先(Dfs)或者广度优先(Bfs)算法,检查每一个可达状态是否满足Φ Φ Φ Φ Φ Φ Φ Φ Φ
上面我们可以看到,不变性可以被视为状态属性,并且可以通过考虑可达状态来检查。但是安全性不能仅考虑可达状态来验证,而是需要对有限路径片段提出要求。
个人理解,不变性的要求是满足所有可达状态满足要求,而安全性是要求所有的系统上出现的有限路径片段满足要求,从这个角度来看,不变性就是安全性的一种特例,如果安全性要求的有限路径片段的长度为1的话,那就变成了不变性要求。
我们考虑一个自动取款机(ATM)的例子,ATM机的要求是,只有在提供了正确的个人识别码(PIN)后,才能从自动取款机中取款。这个属性不是不变量,因为它不是一个单纯的状态属性。但是,它是一种安全性,例如
" 提 供 正 确 的 P I N " , " 取 款 " , . . . "提供正确的PIN","取款",...
" 提 供 正 确 的 P I N " , " 取 款 " , . . .
这样的路径片段是满足安全性的,但如果出现
" 提 供 错 误 的 P I N " , " 取 款 " . . . "提供错误的PIN","取款"...
" 提 供 错 误 的 P I N " , " 取 款 " . . .
这样的路径片段是是不满足安全性的,我们可以看到,一旦出现了这样"坏(bad)"的片段,不管后面如何都是不满足安全性的,我们引入前缀、坏前缀等概念来帮助我们定义安全性。
安全性通常被描述为“不会发生不好的事情 ”(nothing bad should happen)
互斥性 是一种典型的安全性,它要求在临界区最终只有一个进程存在,bad thing指的是在临界区存在两个或两个以上的进程,这种坏事要求永远不会发生无死锁性 (deadlock freedom)是另一个典型的安全属性。在哲学家问题中,发生死锁的特征是所有哲学家都拿起了一把筷子,并且正在等待拿起第二把筷子,这种坏的(或unwanted,即不必要的)情况要求永远都不会发生。
对 于 所 有 的 σ ∈ ( 2 A P ) w ∖ P s a f e 存 在 一 个 σ 的 有 限 前 缀 σ ^ 满 足 P s a f e ∩ { σ ′ ∈ ( 2 A P ) w ∣ σ ^ 是 σ ′ 的 有 限 前 缀 } = ∅ 对于所有的\sigma∈(2^{AP})^w\setminus P_{safe}存在一个\sigma的有限前缀\hat{\sigma}满足 \\ P_{safe}\cap\{\sigma'∈(2^{AP})^w|\hat{\sigma}是\sigma'的有限前缀\}=\varnothing
对 于 所 有 的 σ ∈ ( 2 A P ) w ∖ P s a f e 存 在 一 个 σ 的 有 限 前 缀 σ ^ 满 足 P s a f e ∩ { σ ′ ∈ ( 2 A P ) w ∣ σ ^ 是 σ ′ 的 有 限 前 缀 } = ∅
解释一下,对于所有的无限字σ = A 0 A 1 A 2 . . . ∈ ( 2 A P ) w ∖ P s a f e \sigma=A_{0}A_{1}A_{2}...\in(2^{AP})^w\setminus P_{safe} σ = A 0 A 1 A 2 . . . ∈ ( 2 A P ) w ∖ P s a f e σ \sigma σ σ ^ \hat{\sigma} σ ^ A 0 A 1 . . . A n B n + 1 B n + 2 . . . A_{0}A_{1}...A_{n}B_{n+1}B_{n+2}... A 0 A 1 . . . A n B n + 1 B n + 2 . . . P s a f e P_{safe} P s a f e
有限字 σ ^ = A 0 A 1 . . . A n \hat{\sigma}=A_{0}A_{1}...A_{n} σ ^ = A 0 A 1 . . . A n P s a f e P_{safe} P s a f e B a d P r e f ( P s a f e ) BadPref(P_{safe}) B a d P r e f ( P s a f e )
如果 $\hat{\sigma} $被称为 P s a f e P_{safe} P s a f e σ ^ \hat{\sigma} σ ^ M i n B a d P r e f ( P s a f e ) MinBadPref(P_{safe}) M i n B a d P r e f ( P s a f e )
对于一个TS系统满足安全性,那么当且仅当:
T S ⊨ P s a f e TS\models P_{safe} T S ⊨ P s a f e i f f t r a c e ( T S ) ⊆ P s a f e iff\; trace(TS)\subseteq P_{safe} i f f t r a c e ( T S ) ⊆ P s a f e i f f t r a c e f i n ( T S ) ∩ B a d P r e f = ∅ iff\; trace_{fin}(TS) \cap BadPref=\varnothing i f f t r a c e f i n ( T S ) ∩ B a d P r e f = ∅ i f f t r a c e f i n ( T S ) ∩ M i n B a d P r e f = ∅ iff\; trace_{fin}(TS) \cap MinBadPref=\varnothing i f f t r a c e f i n ( T S ) ∩ M i n B a d P r e f = ∅
以红绿灯系统为例,它拥有一个属性
each red phase should be immediately preceded by a yellow phase
AP定义为{ r e d , y e l l o w } \{red,yellow\} { r e d , y e l l o w }
一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 对 于 所 有 i > 0 满 足 r e d ∈ A i , y e l l o w ∈ A i − 1 一个无限字的集合\{A_{0}A_{1}A_{2}...\}\; 对于所有i>0满足red∈A_{i},yellow∈A_{i-1}
一 个 无 限 字 的 集 合 { A 0 A 1 A 2 . . . } 对 于 所 有 i > 0 满 足 r e d ∈ A i , y e l l o w ∈ A i − 1
类似于∅ ∅ { r e d } \varnothing\varnothing\{red\} ∅ ∅ { r e d } ∅ { r e d } \varnothing\{red\} ∅ { r e d } { r e d } \{red\} { r e d } { y e l l o w } \{yellow\} { y e l l o w }
而类似于{ y e l l o w } { y e l l o w } { r e d } { r e d } ∅ { r e d } \{yellow\}\{yellow\}\{red\}\{red\}\varnothing\{red\} { y e l l o w } { y e l l o w } { r e d } { r e d } ∅ { r e d } { y e l l o w } { y e l l o w } { r e d } { r e d } \{yellow\}\{yellow\}\{red\}\{red\} { y e l l o w } { y e l l o w } { r e d } { r e d }
安全性规定“不好的事情永远不会发生 ”,一个算法可以很容易地实现一个安全性,只要检验一下看看会不会出现不好的情况。但是这很多时候是不需要的,有时候没有必要保证永远不会发生不好的事情,为此需要一些其他属性来补充。这样的属性称为"活性(liveness)"属性。可以说,活性表示**“好事”将会发生**(something good will happen)
“每个进程最终都会进入临界区”
“每个哲学家将会无限经常次吃到饭”
从上面的定义中我们就可以知道,对于活性的判断和安全性完全不同,因为安全性只要有一个坏前缀就可以驳倒安全性,不论后面的序列如何 。而活性需要考虑未来无限路径中需要满足的特性 。
如果 P l i v e P_{live} P l i v e r e f ( P l i v e ) = ( 2 A P ) ∗ ref(P_{live})=(2^{AP})^{*} r e f ( P l i v e ) = ( 2 A P ) ∗ P l i v e P_{live} P l i v e
活性和安全性是不相交的嘛?
是的
所有线性时间属性都是活性或者安全性嘛?
不是
有哪些既不是安全性也不是活性的例子?
例如:“机器在提供三次雪碧之后,会无限次提供啤酒”
这个例子由两个部分组成,一个是“提供三次雪碧之后”,这是一个安全属性,我们给出一个坏前缀,提供一次雪碧后提供啤酒,另一部分是“无限次提供啤酒”,这是一个活性属性。所以这种包含了安全性和活性的特性,既不属于安全性也不属于活性。
是否所有的线性时间属性都可以表示为安全性和活性的交集?
是的
根据分解定理(Decomposition theorem)
对于任何AP上的线性时间属性P,存在安全性P s a f e P_{safe} P s a f e P l i v e P_{live} P l i v e
P = P s a f e ∩ P l i v e P=P_{safe}\cap P_{live}
P = P s a f e ∩ P l i v e
线性时间属性的分类(注:不变性是包含在安全性里面,中间那块黄色的区域既是安全性又是活性,代表的含义是True)
系统的一个重要方面是公平性,公平性排除了被认为是不现实(unrealistic)的无限行为,并且这一步通常是建立活性属性所必需的。
我们通过在并发系统中经常遇到的一个问题来说明公平的概念:
现有一个并发系统N,有进程 P 1 , P 2 . . . P N P_{1},P_{2}...P_{N} P 1 , P 2 . . . P N
从P1开始检查,如果P1请求了服务,那么就为P1提供服务;
如果P1没有请求,那么就检查下一个进程P2,直到检查完毕,然后从头开始检查…
我们可以想见,如果P1一直请求服务,那么Server会为P1无限次提供服务,而剩下的进程都会陷入无限等待的过程,这对除P1外的进程来说是是不公平(unfair)的,这种行为就属于不现实的无限行为。
为了获得由TS建模的并行系统的行为的真实描述,我们需要一种另一种形式的LT属性,来解决TS中不确定性决策的问题。
于是,为了排除上述不现实的行为,我们需要添加公平性约束(Fairness Constraints),而公平的执行或者轨迹(execute or trace)就是满足了某些公平性约束。
公平性约束指定在程序的任何执行中必须经常无限 地访问(或执行)某些状态(某些转换)。
通常,公平性约束用于将程序或其环境约束为**活性(liveness) **,而不涉及有关这些约束的实际实现的细节。
公平约束通过消除不尊重公平约束的执行来减少合法执行的集合。
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ σ = ⟨ s 0 → . . . ⟩ \sigma = \langle s_0 \to ... \rangle σ = ⟨ s 0 → . . . ⟩ P P P σ \sigma σ
情况1:σ \sigma σ ∀ i ∈ N : ∃ j ≥ i : s j ∈ P \forall i \in \mathbb{N} : ∃ j \ge i : s_j \in P ∀ i ∈ N : ∃ j ≥ i : s j ∈ P P 在 σ 中 出 现 无 限 次 P在\sigma中出现无限次 P 在 σ 中 出 现 无 限 次
情况2:σ \sigma σ σ \sigma σ P P P
I n f S ( P , σ ) Inf_S(P,\sigma) I n f S ( P , σ ) P P P σ \sigma σ
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ σ = ⟨ s 0 → . . . ⟩ \sigma = \langle s_0 \to ... \rangle σ = ⟨ s 0 → . . . ⟩ Q Q Q σ \sigma σ
情况1:σ \sigma σ ∀ i ∈ N : ∃ j ≥ i : s j → s j + 1 ∈ Q \forall i \in \mathbb{N} : ∃ j \ge i : s_j \to s_{j+1} \in Q ∀ i ∈ N : ∃ j ≥ i : s j → s j + 1 ∈ Q Q 在 σ 中 出 现 无 限 次 Q在\sigma中出现无限次 Q 在 σ 中 出 现 无 限 次
情况2:σ \sigma σ σ \sigma σ Q Q Q
I n f T ( Q , σ ) Inf_T(Q,\sigma) I n f T ( Q , σ ) Q Q Q σ \sigma σ
例(循环状态):
s 1 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ω ⟩ s_1 \; is\;recurrent\;in\;⟨(s_0 → s_1 → s_3)^ω⟩ s 1 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ω ⟩
s 1 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 → s 0 → s 2 → s 3 ) ω ⟩ s_1 \; is\;recurrent\;in\;⟨(s_0 → s_1 → s_3 \to s_0 \to s_2 \to s_3)^ω⟩ s 1 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 → s 0 → s 2 → s 3 ) ω ⟩
s 1 i s N O T r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ∗ → ( s 0 → s 2 → s 3 ) ω ⟩ s_1 \; is\;NOT\;recurrent\;in\;⟨(s_0 → s_1 → s_3)^* \to (s_0 \to s_2 \to s_3)^ω⟩ s 1 i s N O T r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ∗ → ( s 0 → s 2 → s 3 ) ω ⟩
个人理解,这里在说循环状态时有两个判断标准:
当这段执行是无限 的时,该状态应该在这段无限执行内 ;
当这段执行是有限 的时,该状态应该是这段有限执行的最终状态 。
下列循环转换可类比于循环状态
s 1 → s 3 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 → s 0 → s 2 → s 3 ) ω ⟩ s_1 \to s_3 \; is\;recurrent\;in\;⟨(s_0 → s_1 → s_3 \to s_0 \to s_2 \to s_3)^ω⟩ s 1 → s 3 i s r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 → s 0 → s 2 → s 3 ) ω ⟩
s 1 → s 3 i s N O T r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ∗ → ( s 0 → s 2 → s 3 ) ω ⟩ s_1 \to s_3 \; is\;NOT\;recurrent\;in\;⟨(s_0 → s_1 → s_3)^* \to (s_0 \to s_2 \to s_3)^ω⟩ s 1 → s 3 i s N O T r e c u r r e n t i n ⟨ ( s 0 → s 1 → s 3 ) ∗ → ( s 0 → s 2 → s 3 ) ω ⟩
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ σ σ σ I n f S ( F , σ ) Inf_S (F, σ) I n f S ( F , σ )
例:
E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩ Exec(S) = ⟨{s_0}^ω⟩,⟨{s_0}^+ \to s_1⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^w⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^+ \to s_5⟩ E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩
满足 { s 0 } \{s_0\} { s 0 } ⟨ s 0 ω ⟩ ⟨{s_0}^ω⟩ ⟨ s 0 ω ⟩
满足 { s 1 , s 4 } \{s_1, s_4\} { s 1 , s 4 } ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ ⟨{s_0}^+ \to s_1⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^w⟩ ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩
满足 { s 1 , s 5 } \{s_1, s_5\} { s 1 , s 5 } ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩ ⟨{s_0}^+ \to s_1⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^+ \to s_5⟩ ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩
满足 { s 0 , s 1 } \{s_0, s_1\} { s 0 , s 1 } 分别满足 { s 0 } \{s_0\} { s 0 } { s 1 } \{s_1\} { s 1 }
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩ { F i } i ∈ J \{F_i\}i ∈ J { F i } i ∈ J
任何执行 σ σ σ ∀ i ∈ J : I n f S ( F i , σ ) ∀i ∈ J : Inf_S (F_i, σ) ∀ i ∈ J : I n f S ( F i , σ )
例:
E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 w ⟩ , ⟨ ( s 0 + → s 1 + ) w ⟩ , ⟨ ( s 0 + → s 1 + ) ∗ → s 0 + → s 1 w ⟩ Exec(S) = ⟨{s_0}^ω⟩,⟨{s_0}^+ \to {s_1}^w⟩,⟨({s_0}^+ \to {s_1}^+)^w⟩,⟨({s_0}^+ \to {s_1}^+)^* \to {s_0}^+ \to {s_1}^w⟩ E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 w ⟩ , ⟨ ( s 0 + → s 1 + ) w ⟩ , ⟨ ( s 0 + → s 1 + ) ∗ → s 0 + → s 1 w ⟩
满足 { s 0 } \{s_0\} { s 0 } ⟨ s 0 ω ⟩ , ⟨ ( s 0 + → s 1 + ) w ⟩ ⟨{s_0}^ω⟩, ⟨({s_0}^+ \to {s_1}^+)^w⟩ ⟨ s 0 ω ⟩ , ⟨ ( s 0 + → s 1 + ) w ⟩
满足 { s 0 , s 1 } \{s_0, s_1\} { s 0 , s 1 } E x e c ( S ) Exec(S) E x e c ( S )
满足 { s 0 } { s 1 } \{s_0\}\{s_1\} { s 0 } { s 1 } 多重公平性 的执行是:⟨ ( s 0 + → s 1 + ) w ⟩ ⟨({s_0}^+ \to {s_1}^+)^w⟩ ⟨ ( s 0 + → s 1 + ) w ⟩
满足 { s 0 } { s 1 } \{s_0\}\{s_1\} { s 0 } { s 1 } 多重公平性 意味着同时满足 { s 0 } \{s_0\} { s 0 } { s 1 } \{s_1\} { s 1 }
简单情况:J J J ∣ J ∣ |J| ∣ J ∣ J J J
下面的简单公平性系统⟨ S ′ , I ′ , R ′ ⟩ ⟨S', I', R'⟩ ⟨ S ′ , I ′ , R ′ ⟩
S ′ = S × J S' = S \times J S ′ = S × J I ′ = I × { 0 } I' = I \times \{0\} I ′ = I × { 0 } R ′ = { ( ⟨ s , j ⟩ , ⟨ s ′ , j + 1 m o d ∣ J ∣ ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , j ⟩ , ⟨ s ′ , j ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∉ F j } \begin{aligned} R' = &\{ (⟨s,j⟩,⟨s',j+1 \mod |J|⟩) | (s,s') \in R \land s \in F_j\}\\ &∪ \{(⟨s, j⟩,⟨s', j⟩) |(s,s') ∈ R ∧ s \notin F_j \} \end{aligned} R ′ = { ( ⟨ s , j ⟩ , ⟨ s ′ , j + 1 m o d ∣ J ∣ ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , j ⟩ , ⟨ s ′ , j ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ / F j } 简单公平状态F ′ = F 0 × { 0 } F' = F_0 \times \{0\} F ′ = F 0 × { 0 }
例:
带有多重公平性F 0 = { s 0 } F_0 = \{s_0\} F 0 = { s 0 } { ( s 0 , 0 ) } \{(s_0,0)\} { ( s 0 , 0 ) }
一般情况(J 可能无限)。
下面的简单公平性系统⟨ S ′ , I ′ , R ′ ⟩ ⟨S', I', R'⟩ ⟨ S ′ , I ′ , R ′ ⟩
S ′ = S × J × J S' = S \times J \times J S ′ = S × J × J
I ′ = I × { 0 } × { 0 } I' = I \times \{0\} \times \{0\} I ′ = I × { 0 } × { 0 }
R ′ = { ( ⟨ s , i , i ⟩ , ⟨ s ′ , i ⊕ 1 , 0 ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , i , j ⟩ , ⟨ s ′ , i , j + 1 ⟩ ) ∣ j < i ∧ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , i , j ⟩ , ⟨ s ′ , i , j ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∉ F j } \begin{aligned} R' = &\{ (⟨s,i,i⟩,⟨s',i⊕1,0⟩) | (s,s') \in R \land s \in F_j\}\\ &∪ \{(⟨s,i,j⟩,⟨s',i,j+1⟩) | j < i \land (s,s') \in R \land s \in F_j\} \\&∪ \{(⟨s,i,j⟩,⟨s',i,j⟩) |(s,s') ∈ R ∧ s \notin F_j \} \end{aligned} R ′ = { ( ⟨ s , i , i ⟩ , ⟨ s ′ , i ⊕ 1 , 0 ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , i , j ⟩ , ⟨ s ′ , i , j + 1 ⟩ ) ∣ j < i ∧ ( s , s ′ ) ∈ R ∧ s ∈ F j } ∪ { ( ⟨ s , i , j ⟩ , ⟨ s ′ , i , j ⟩ ) ∣ ( s , s ′ ) ∈ R ∧ s ∈ / F j }
简单公平状态F ′ = F 0 × J × { 0 } F' = F_0 \times J \times \{0\} F ′ = F 0 × J × { 0 }
注:$ i⊕1 \triangleq \begin{cases} i+1;(if;J是无限的) \ i+1 \mod |J| ;(else)\end{cases}$
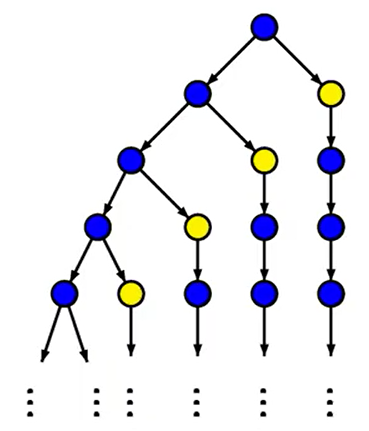
在公平执行中,计数器 i、j 形成一个三角形:⟨ ( 0 , 0 ) → ( 1 , 0 ) → ( 1 , 1 ) → ( 2 , 0 ) → ( 2 , 1 ) → ( 2 , 2 ) → ( 3 , 0 ) → . . . ⟩ ⟨(0, 0) → (1, 0) → (1, 1) → (2, 0) → (2, 1) → (2, 2) → (3, 0) → ...⟩ ⟨ ( 0 , 0 ) → ( 1 , 0 ) → ( 1 , 1 ) → ( 2 , 0 ) → ( 2 , 1 ) → ( 2 , 2 ) → ( 3 , 0 ) → . . . ⟩
例:带有多重公平性F 0 = { s 0 } F_0 = \{s_0\} F 0 = { s 0 } { ( s 0 , 0 , 0 ) } \{(s_0,0,0)\} { ( s 0 , 0 , 0 ) } { ( s 0 , 1 , 0 ) } \{(s_0,1,0)\} { ( s 0 , 1 , 0 ) }
令 ⟨ S , I , R ⟩ ⟨S, I, R⟩ ⟨ S , I , R ⟩
任何执行 σ 必须满足 I n f S ( F , σ ) ⇒ I n f S ( G , σ ) Inf_S (F, σ) ⇒ Inf_S (G, σ) I n f S ( F , σ ) ⇒ I n f S ( G , σ ) F F F σ σ σ G G G σ σ σ
例:
E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩ Exec(S) = ⟨{s_0}^ω⟩,⟨{s_0}^+ \to s_1⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^w⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^+ \to s_5⟩ E x e c ( S ) = ⟨ s 0 ω ⟩ , ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩
满足 ${s_0} ⇒ {s_5} $ 简单公平性的执行是:⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩ ⟨{s_0}^+ \to s_1⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^w⟩,⟨{s_0}^+ \to s_2 \to (s_3 \to s_4) ^+ \to s_5⟩ ⟨ s 0 + → s 1 ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) w ⟩ , ⟨ s 0 + → s 2 → ( s 3 → s 4 ) + → s 5 ⟩
满足 ${s_3} ⇒ {s_4} $ 简单公平性的执行是:E x e c ( S ) Exec(S) E x e c ( S )
满足 { s 3 } ⇒ { s 4 } \{s_3\} ⇒ \{s_4\} { s 3 } ⇒ { s 4 }
如何表述这类公平性约束?这里采用基于动作 A \mathcal{A} A
弱可能性 ( W F WF W F
我们说,一个 TLA 的 Action 动作 A \mathcal{A} A s s s t t t s s s ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ ⟨上一个状态\;s, 下一个状态\;t⟩ ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ A ⟨ s → t ⟩ \mathcal{A}⟨s\to t⟩ A ⟨ s → t ⟩
W F f ( A ) WF_f(\mathcal{A}) W F f ( A ) A ∧ ( f ′ ≠ f ) \mathcal{A} ∧ (f' \neq f) A ∧ ( f ′ = f ) A ∧ ( f ′ ≠ f ) \mathcal{A} ∧ (f' \neq f) A ∧ ( f ′ = f ) 换言之, 如果一旦出现一个 Action 动作的可能性 并且一直保持着这种系统会执行这个动作的可能性 ,那么就一定会出现和发生 ,或者说,被执行无限多次 。
强可能性 ( S F SF S F
TLA 规约另外也定义了强公平性 (Strong Fairness) S F f ( A ) SF_f (\mathcal{A}) S F f ( A ) f f f A \mathcal{A} A A ∧ ( f ′ ≠ f ) \mathcal{A} ∧ (f' \neq f) A ∧ ( f ′ = f ) 存在着 无限频繁多次的可能性,那么 A ∧ ( f ′ ≠ f ) \mathcal{A} ∧ (f' \neq f) A ∧ ( f ′ = f ) 如果一个动作范式在某个时间点变得永远可能,那么 也满足“无限经常”的条件。 因此,强公平性 S F f ( A ) SF_f(\mathcal{A}) S F f ( A ) W F f ( A ) WF_f(\mathcal{A}) W F f ( A )
个人理解:
在弱可能性 W F f ( A ) WF_f(\mathcal{A}) W F f ( A ) A \mathcal{A} A ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ ⟨上一个状态\;s, 下一个状态\;t⟩ ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ s → t s \to t s → t s s s A \mathcal{A} A 则该动作 A \mathcal{A} A 。
在强可能性 S F f ( A ) SF_f(\mathcal{A}) S F f ( A ) A \mathcal{A} A ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ ⟨上一个状态\;s, 下一个状态\;t⟩ ⟨ 上 一 个 状 态 s , 下 一 个 状 态 t ⟩ s → t s \to t s → t s s s A \mathcal{A} A 则该动作 A \mathcal{A} A 。
公平属性是 前提条件 施加在系统上以排除不切实际的痕迹。
无条件公平的形式是**“每个过程都会无休止地轮流使用”**。
强公平性 (SF) 的形式是**“如果无限频繁地启用它,则每个过程都将无限次地轮流运行”**。
弱公平性 (WF) 的形式是**“如果从某个特定点连续进行,则每个过程都会无限制地轮流转动”**。
之前我们看到了,LTL公式可以用来描述两进程互斥问题的公平性属性,现在我们将它推广到一般的公平性问题
设 ϕ \phi ϕ ψ \psi ψ
无条件的公平性:□ ◊ ψ \Box\Diamond\psi □ ◊ ψ
强公平性:□ ◊ ϕ → □ ◊ ψ \Box\Diamond\phi\rightarrow\Box\Diamond\psi □ ◊ ϕ → □ ◊ ψ
弱公平性:◊ □ ϕ → □ ◊ ψ \Diamond\Box\phi\rightarrow\Box\Diamond\psi ◊ □ ϕ → □ ◊ ψ
对于公平性假设fair和LTL公式 ϕ \phi ϕ
s ⊨ f a i r ϕ 当且仅当 对于所有的π∈Paths(s),如果 π ⊨ f a i r , 那 么 π ⊨ ϕ 当且仅当 s ⊨ ( f a i r → ϕ ) s\vDash_{fair}\phi \\ \text{当且仅当 对于所有的π∈Paths(s),如果}π\vDash fair,那么π\vDash\phi \\ \text{当且仅当 }s\vDash (fair\rightarrow\phi)
s ⊨ f a i r ϕ 当且仅当 对于所有的 π∈Paths(s), 如果 π ⊨ f a i r , 那 么 π ⊨ ϕ 当且仅当 s ⊨ ( f a i r → ϕ )
其实这里想要表达的意思是,如果我们有了一套算法或者说流程可以验证TS系统是否满足LTL公式,那么我们可以用相同的流程步骤来检测在加入公平性约束的情况下,TS系统是否满足LTL公式。
对于一个没有终止状态的T S = ⟨ S , I , R ⟩ TS=⟨S,I,R⟩ T S = ⟨ S , I , R ⟩ , T S 上 的 无 限 执 行 片 段 ,TS上的无限执行片段 , T S 上 的 无 限 执 行 片 段
如果ρ \rho ρ 无条件公平性(unconditionally A-fair) ,那么无论何时
if ∃ ∞ j ≥ 0 , a j ∈ A . \text{if }\overset{∞}∃ j\ge 0,a_{j}∈A.
if ∃ ∞ j ≥ 0 , a j ∈ A .
无条件A-fair的含义是,无论在什么情况下,A中的动作总能无限经常次执行。
如果ρ \rho ρ 强公平性(strongly A-fair) ,那么无论何时
( ∃ ∞ j . A c t ( s j ∩ A ≠ ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A ) (\overset{∞}∃ j.Act(s_{j}\cap A\ne ∅)\Rightarrow(\text{if }\overset{∞}∃ j\ge 0,a_{j}∈A)
( ∃ ∞ j . A c t ( s j ∩ A = ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A )
strongly A-fair的含义是,存在无限经常次A为enabled时,A中动作将会无限经常次执行 。
如果ρ \rho ρ 弱公平性(weakly A-fair) ,那么无论何时
( ∀ ∞ j . A c t ( s j ∩ A ≠ ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A ) (\overset{∞}\forall j.Act(s_{j}\cap A\ne ∅)\Rightarrow(\text{if }\overset{∞}∃ j\ge 0,a_{j}∈A)
( ∀ ∞ j . A c t ( s j ∩ A = ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A )
weakly A-fair的含义是,从某个时刻起,A将会为enabled,从而A中动作将会无限经常次执行 。
strong和weak引入了enabled这个概念,
strongly A-fair要求在enable的片段中动作能够无限经常次执行,而在not enabled的片段中没有规定
weakly A-fair则是,不管之前如何,如果在某一个时间点之后,动作持续一直enabled,那么在这片段中动作要求能够无限经常次执行。
从上面的定义中我们可以容易得到
unconditionally A-fair ⇒ strongly A-fair ⇒ weakly A-fair \text{unconditionally A-fair}\Rightarrow \text{strongly A-fair}\Rightarrow \text{weakly A-fair}
unconditionally A-fair ⇒ strongly A-fair ⇒ weakly A-fair
L T L LTL L T L 时间逻辑TL:用以表达与系统执行相关的属性。不能表达没有明确的转换关系,没有初始状态的概念。
TL逻辑定义为:
一种语法:经典逻辑运算符加上时间运算符来谈论未来和过去。
语义:对象域(称为模型),我们将在其上测试公式的有效性,以及运算符的解释。
LTL 公式总是与系统的给定迹 σ σ σ 迹构成该逻辑的模型。
注意:我们经常说即时而不是状态,以指定迹 σ σ σ
s s s 当前时刻成立 ,在轨迹表现为在第一个位置成立¬ P \neg P ¬ P P ∨ Q P \lor Q P ∨ Q P ∧ Q P \land Q P ∧ Q ◯ P \bigcirc P ◯ P 下一个时刻成立 ,在轨迹表现为第二个位置成立□ P \Box P □ P P总是(always)成立 ,即在全部的时刻都成立 ,在轨迹上表现为每个位置都成立,□ P = ¬ ◊ ¬ P \Box P=\lnot \Diamond \lnot P □ P = ¬ ◊ ¬ P ◊ P \Diamond P ◊ P P最终(eventually)能够成立 ,在轨迹上表现为,在某一个时刻的时候P成立 ,◊ P = ¬ □ ¬ P \Diamond P = \lnot \Box \lnot P ◊ P = ¬ □ ¬ P P P P → \to → P P P F F F ◊ □ P \Diamond \Box P ◊ □ P F F F □ ◊ P \Box \Diamond P □ ◊ P F F F E x e c Exec E x e c σ \sigma σ F F F P U Q P \mathcal{U} Q P U Q 直到Q成立前,P一直成立 P ⇝ Q P \rightsquigarrow Q P ⇝ Q 当P成立时,Q一会后也成立 。如果 P P P Q Q Q
最小的运算符是◯ P \bigcirc P ◯ P P U Q P \mathcal{U}Q P U Q
◊ P ≜ T r u e U P \Diamond P \triangleq True \; \mathcal{U} P ◊ P ≜ T r u e U P □ P ≜ ¬ ◊ ¬ P \Box P \triangleq \neg \Diamond \neg P □ P ≜ ¬ ◊ ¬ P P ⇝ Q ≜ □ ( P ⇒ ◊ Q ) P \rightsquigarrow Q \triangleq \Box (P ⇒ \Diamond Q) P ⇝ Q ≜ □ ( P ⇒ ◊ Q )
我们可以使用另一种语法:
□ ↔ G \Box ↔ G □ ↔ G ◊ ↔ F \Diamond ↔ F ◊ ↔ F ◯ ↔ X \bigcirc↔ X ◯ ↔ X
运算符 wating-for(或 unless 或 weak-less): Q 可能最终为真,同时 P 仍然为真
P W Q ≜ □ P ∨ P U Q P\; \mathcal{W}\;Q \triangleq \Box P ∨ P \mathcal{U}Q P W Q ≜ □ P ∨ P U Q
P R Q ≜ Q U ( P ∧ Q ) P \; \mathcal{R} \; Q \triangleq Q \mathcal{U}(P ∧ Q) P R Q ≜ Q U ( P ∧ Q )
⊖ P \ominus P ⊖ P previous : P 在前一个瞬间为真⊟ P \boxminus P ⊟ P has-always-been : P 一直是真实的直到当前时刻$ \diamond P$:once : P 在过去是真的
P S Q P\; \mathcal{S}\;Q P S Q since : 自 Q 过去一直为真,而 P 自上次出现 Q 以来一直为真P B Q P\; \mathcal{B}\;Q P B Q back-to : P 自上次出现 Q 以来为真,或者如果 Q 从未为真,则自初始时刻起为真
我们用 ( σ , i ) (σ, i) ( σ , i ) ⟨ s i → s i + 1 → . . . ⟩ ⟨s_i → s_i+1 → ...⟩ ⟨ s i → s i + 1 → . . . ⟩ σ = ⟨ s 0 → s 1 → . . . ⟩ σ = ⟨s0 → s1 → ...⟩ σ = ⟨ s 0 → s 1 → . . . ⟩
系统 S S S F F F S S S
∀ σ ∈ E x e c ( S ) : ( σ , 0 ) ⊨ F S ⊨ F \frac{\forall σ \in Exec(S):(σ,0) \models F}{S \models F}
S ⊨ F ∀ σ ∈ E x e c ( S ) : ( σ , 0 ) ⊨ F
P ∧ Q P\land Q P ∧ Q ( σ , i ) ⊨ P ∧ Q (\sigma,i) \models P \land Q ( σ , i ) ⊨ P ∧ Q ( σ , i ) ⊨ P (\sigma ,i) \models P ( σ , i ) ⊨ P 并且 ( σ , i ) ⊨ Q (\sigma ,i) \models Q ( σ , i ) ⊨ Q
( σ , i ) ⊨ P ( σ , i ) ⊨ Q ( σ , i ) ⊨ P ∧ Q \frac{(\sigma,i) \models P\qquad(\sigma,i) \models Q}{(\sigma,i) \models P \land Q}
( σ , i ) ⊨ P ∧ Q ( σ , i ) ⊨ P ( σ , i ) ⊨ Q
P ∨ Q P\lor Q P ∨ Q ( σ , i ) ⊨ P ∧ Q (\sigma,i) \models P \land Q ( σ , i ) ⊨ P ∧ Q ( σ , i ) ⊨ P (\sigma ,i) \models P ( σ , i ) ⊨ P 或者 ( σ , i ) ⊨ Q (\sigma ,i) \models Q ( σ , i ) ⊨ Q
( σ , i ) ⊨ P ( σ , i ) ⊨ P ∨ Q ( σ , i ) ⊨ Q ( σ , i ) ⊨ P ∨ Q \frac{(\sigma,i) \models P}{(\sigma,i) \models P \lor Q} \qquad
\frac{(\sigma,i) \models Q}{(\sigma,i) \models P \lor Q}
( σ , i ) ⊨ P ∨ Q ( σ , i ) ⊨ P ( σ , i ) ⊨ P ∨ Q ( σ , i ) ⊨ Q
¬ P \neg P ¬ P ¬ ( σ , i ) ⊨ P ( σ , i ) ⊨ ¬ P \frac{\neg (\sigma,i) \models P}{(\sigma,i) \models \neg P}
( σ , i ) ⊨ ¬ P ¬ ( σ , i ) ⊨ P
s s s σ i = s ( σ , i ) ⊨ s \frac{\sigma_i=s}{(\sigma,i) \models s}
( σ , i ) ⊨ s σ i = s
◯ P \bigcirc P ◯ P ( σ , i ) ⊨ ◯ P (\sigma,i) \models \bigcirc P ( σ , i ) ⊨ ◯ P s u f f i x ( σ , 1 ) = σ 1 , σ 2 , σ 3 . . . ⊨ P suffix(\sigma,1) = \sigma_{1},\sigma_{2},\sigma_{3}...\models P s u f f i x ( σ , 1 ) = σ 1 , σ 2 , σ 3 . . . ⊨ P
( σ , i + 1 ) ⊨ P ( σ , i ) ⊨ ◯ P \frac{(\sigma,i+1) \models P}{(\sigma,i) \models \bigcirc P}
( σ , i ) ⊨ ◯ P ( σ , i + 1 ) ⊨ P
P U Q P\;\mathcal{U}\;Q P U Q ( σ , i ) ⊨ P U Q (\sigma,i) \models P\;\mathcal{U}\;Q ( σ , i ) ⊨ P U Q j ≥ 0 j \ge 0 j ≥ 0 s u f f i x ( σ , j ) = σ j , σ j + 1 , σ j + 2 . . . ⊨ Q suffix(\sigma,j)=\sigma_{j},\sigma_{j+1},\sigma_{j+2}...\models Q s u f f i x ( σ , j ) = σ j , σ j + 1 , σ j + 2 . . . ⊨ Q s u f f i x ( σ , i ) = σ i , σ i + 1 , σ i + 2 . . . ⊨ P suffix(\sigma,i)=\sigma_{i}, \sigma_{i+1}, \sigma_{i+2}...\models P s u f f i x ( σ , i ) = σ i , σ i + 1 , σ i + 2 . . . ⊨ P 0 ≤ i < 1 0\le i\lt 1 0 ≤ i < 1
{ ∃ k ≥ 0 : ( σ , i + k ) ⊨ Q } ∧ { ∀ k ′ , 0 ≤ k ′ ≤ k : ( σ , i + k ′ ) ⊨ P } ( σ , i ) ⊨ P U Q \frac{\{∃ k \ge 0:(\sigma,i+k) \models Q\} \land \{ \forall k',0 \le k' \le k:(\sigma, i+k')\models P\} } {(\sigma,i) \models P \mathcal{U} Q}
( σ , i ) ⊨ P U Q { ∃ k ≥ 0 : ( σ , i + k ) ⊨ Q } ∧ { ∀ k ′ , 0 ≤ k ′ ≤ k : ( σ , i + k ′ ) ⊨ P }
◊ P \Diamond P ◊ P ( σ , i ) ⊨ ◊ P (\sigma,i) \models \Diamond P ( σ , i ) ⊨ ◊ P 存在 i ≥ 0 i \ge 0 i ≥ 0 σ j , σ j + 1 , σ j + 2 . . . ⊨ P \sigma_{j},\sigma_{j+1},\sigma_{j+2}...\models P σ j , σ j + 1 , σ j + 2 . . . ⊨ P
∃ k ≥ 0 : ( σ , i + k ) ⊨ P ( σ , i ) ⊨ ◊ P \frac{∃k \ge 0 :(\sigma ,i+k) \models P}{(\sigma,i) \models \Diamond P}
( σ , i ) ⊨ ◊ P ∃ k ≥ 0 : ( σ , i + k ) ⊨ P
□ P \Box P □ P ( σ , i ) ⊨ □ P (\sigma,i) \models \Box P ( σ , i ) ⊨ □ P 对所有 i ≥ 0 i \ge 0 i ≥ 0 σ j , σ j + 1 , σ j + 2 . . . ⊨ P \sigma_{j},\sigma_{j+1},\sigma_{j+2}...\models P σ j , σ j + 1 , σ j + 2 . . . ⊨ P
∀ k ≥ 0 : ( σ , i + k ) ⊨ P ( σ , i ) ⊨ □ P \frac{\forall k \ge 0 :(\sigma ,i+k) \models P}{(\sigma,i) \models \Box P}
( σ , i ) ⊨ □ P ∀ k ≥ 0 : ( σ , i + k ) ⊨ P
P ⇝ Q P \rightsquigarrow Q P ⇝ Q { ∀ k ≥ 0 : ( σ , i + k ) ⊨ P } ⇒ { ∃ k ′ ≥ k : ( σ , i + k ′ ) ⊨ Q } ( σ , i ) ⊨ P ⇝ Q \frac{\{\forall k \ge 0 :(\sigma ,i+k) \models P \} \Rightarrow \{∃ k' \ge k :(\sigma ,i+k') \models Q\} } { (\sigma,i) \models P \rightsquigarrow Q}
( σ , i ) ⊨ P ⇝ Q { ∀ k ≥ 0 : ( σ , i + k ) ⊨ P } ⇒ { ∃ k ′ ≥ k : ( σ , i + k ′ ) ⊨ Q }
线性时序逻辑具有这样的表达能力,以至于它可以准确地表示根据转换系统描述的任何操作规范,因此:
检查变迁系统 M 是否具有时间属性 F S p e c F_{\mathcal{S}pec} F S p e c
M ⊨ F S p e c \mathcal{M} \models F_{\mathcal{S}pec}
M ⊨ F S p e c
无公平性
简单公平性(s 1 , s 2 s_1,s_2 s 1 , s 2
s 0 ∧ ◯ s 0 s_0 \land \bigcirc s_0 s 0 ∧ ◯ s 0 $n (s_0→{s_1}^ω) $
n
s 0 ∧ ◯ ( s 0 ∨ s 1 ) s_0 \land \bigcirc (s_0 \lor s_1) s 0 ∧ ◯ ( s 0 ∨ s 1 ) o
o
□ ( s 0 ⇒ ◯ s 0 ) \Box (s_0 ⇒ \bigcirc s_0) □ ( s 0 ⇒ ◯ s 0 ) $n (s_0→{s_1}^ω) $
n
□ ( s 0 ⇒ ◯ ( s 0 ∨ s 1 ) \Box (s_0 ⇒ \bigcirc (s_0 \lor s_1) □ ( s 0 ⇒ ◯ ( s 0 ∨ s 1 ) o
o
□ ( s 0 ⇒ ◯ s 1 ) \Box (s_0 ⇒ \bigcirc s_1) □ ( s 0 ⇒ ◯ s 1 ) o
o
◊ ( s 0 ⇒ ◯ s 1 ) \Diamond (s_0 ⇒ \bigcirc s_1) ◊ ( s 0 ⇒ ◯ s 1 ) $n ({s_0}^ω) $
o
□ s 0 \Box s_0 □ s 0 $n (s_0→{s_1}^ω) $
n
◊ ¬ s 0 \Diamond \neg s_0 ◊ ¬ s 0 $n ({s_0}^ω) $
o
◊ □ s 0 \Diamond \Box s_0 ◊ □ s 0 $n ({s_0}^ω) $
o
s 0 W s 1 s_0 \mathcal{W} s_1 s 0 W s 1 o
o
s 0 U s 1 s_0 \mathcal{U} s_1 s 0 U s 1 $n ({s_0}^ω) $
o
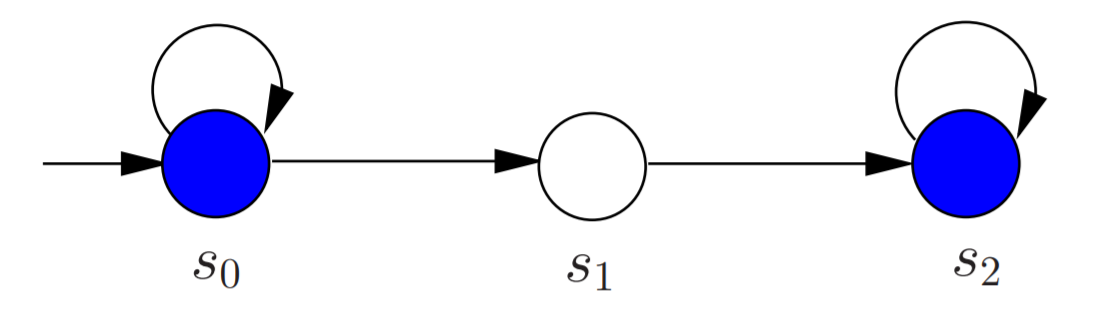
E x e c ( S ) = ⟨ s 0 → s 1 w ⟩ , ⟨ ( s 0 → s 1 + ) w ⟩ , ⟨ ( s 0 → s 1 + ) + → s 2 w ⟩ Exec(S) = ⟨s_0 \to {s_1}^w⟩, ⟨(s_0 \to {s_1}^+)^w⟩, ⟨(s_0 \to {s_1}^+)^+ \to {s_2}^w⟩ E x e c ( S ) = ⟨ s 0 → s 1 w ⟩ , ⟨ ( s 0 → s 1 + ) w ⟩ , ⟨ ( s 0 → s 1 + ) + → s 2 w ⟩
无公平性
W e a k F a i r n e s s ( s 1 , s 2 ) \mathcal{W_{eak}F_{airness}}(s_1,s_2) W e a k F a i r n e s s ( s 1 , s 2 ) S t r o n g F a i r n e s s ( s 1 , s 2 ) \mathcal{S_{trong}F_{airness}}(s_1,s_2) S t r o n g F a i r n e s s ( s 1 , s 2 )
□ ◊ ¬ s 1 \Box \Diamond \neg s_1 □ ◊ ¬ s 1 $n (s_0→{s_1}^ω) $
o
o
□ ( s 1 ⇒ ◊ s 2 ) \Box (s_1 ⇒ \Diamond s_2) □ ( s 1 ⇒ ◊ s 2 ) $n (s_0→{s_1}^ω) $
$n ((s_0→s_1)^ω) $
o
◊ □ ( s 1 ∨ s 2 ) \Diamond \Box (s_1 \lor s_2) ◊ □ ( s 1 ∨ s 2 ) $n ((s_0→s_1)^ω) $
n
o
□ ( s 1 U s 2 ) \Box (s_1 \mathcal{U} s_2) □ ( s 1 U s 2 ) $n (s_0→…) $
n
n
□ ( s 0 ⇒ s 0 U s 1 ) \Box (s_0 ⇒ s_0 \mathcal{U} s_1) □ ( s 0 ⇒ s 0 U s 1 ) o
o
o
□ ( s 0 U ( s 1 ∨ s 2 ) ) \Box(s_0 \mathcal{U} (s_1 \lor s_2)) □ ( s 0 U ( s 1 ∨ s 2 ) ) o
o
o
□ ( s 1 ⇒ s 1 U s 2 ) \Box (s_1 ⇒ s_1 \mathcal{U} s_2) □ ( s 1 ⇒ s 1 U s 2 ) $n (s_0→{s_1}^ω) $
$n ((s_0→s_1)^ω) $
$n (s0→s1→s0→s1→s2^ω) $
◊ ( s 1 U s 2 ) \Diamond (s_1 \mathcal{U} s_2) ◊ ( s 1 U s 2 ) $n (s_0→{s_1}^ω) $
$n ((s_0→s_1)^ω) $
o
◊ ( s 1 W s 2 ) \Diamond (s_1 \mathcal{W} s_2) ◊ ( s 1 W s 2 ) $n ((s_0→s_1)^ω) $
n
o
□ ◊ ( s 1 U ( s 0 ∨ s 2 ) ) \Box \Diamond (s_1 \mathcal{U} (s_0 \lor s_2)) □ ◊ ( s 1 U ( s 0 ∨ s 2 ) ) $n (s_0→{s_1}^ω) $
o
o
个人理解:以例1中的第一行 $\Box \Diamond \neg s_1 $ 为例,可以将其视为一个条件,意为在该条件下是否满足“无公平性” 和 “W F ( s 1 , s 2 ) WF(s_1,s_2) W F ( s 1 , s 2 )
$\Box \Diamond \neg s_1 $ 意为 “对于所有迹,最终都会不出现 s 1 s_1 s 1
对于“无公平性”:由图可见存在一个迹 σ = ⟨ s 0 → s 1 w ⟩ \sigma = ⟨s_0 \to {s_1}^w⟩ σ = ⟨ s 0 → s 1 w ⟩ n(means no)。
对于“W F ( s 1 , s 2 ) WF(s_1, s_2) W F ( s 1 , s 2 ) s 0 → s 1 s_0 \to s_1 s 0 → s 1 总是成立
对于“S F ( s 1 , s 2 ) SF(s_1, s_2) S F ( s 1 , s 2 ) s 0 → s 1 s_0 \to s_1 s 0 → s 1 会成立
没有什么不好的事情发生(详见第三部分 )= 在执行的有限前缀上无效的属性:
□ P \Box P □ P □ ( P ⇒ □ P ) \Box (P ⇒ \Box P) □ ( P ⇒ □ P ) P W Q P \mathcal{W} Q P W Q
美好的事情终会发生 = 始终可以通过扩展运行前缀来验证的属性:
◊ P \Diamond P ◊ P P ⇝ Q P \rightsquigarrow Q P ⇝ Q
一些活性与安全性的组合属性,例如
P U Q P \mathcal{U} Q P U Q □ P ∧ ◊ Q \Box P \land \Diamond Q □ P ∧ ◊ Q Reponse: □ ◊ P \Box \Diamond P □ ◊ P
Persistance: ◊ □ P \Diamond \Box P ◊ □ P
指定系统可达状态的超集(详见第三部分 :
S ⊨ □ P \mathcal{S} \models \Box P
S ⊨ □ P
其中 P 是状态谓词。
指定情况发生时的稳定性:
S ⊨ □ ( P ⇒ □ P ) \mathcal{S} \models \Box(P ⇒ \Box P)
S ⊨ □ ( P ⇒ □ P )
其中 P 是状态谓词
指定在某个执行中可能达到满足 P P P
对于 σ σ σ σ ⊨ ¬ P ≡ σ ⊭ P σ \models ¬P ≡ σ \nvDash P σ ⊨ ¬ P ≡ σ ⊭ P
对于 S \mathcal{S} S S ⊨ ¬ P ⇒ S ⊭ P \mathcal{S} \models ¬P ⇒ \mathcal{S} \nvDash P S ⊨ ¬ P ⇒ S ⊭ P
S ⊭ P \mathcal{S} \nvDash P S ⊭ P ¬ Q ¬Q ¬ Q
在 LTL 中,我们可以有$ S \nvDash Q ∧ S \nvDash ¬Q$ :
指定 P P P
S ⊨ □ ◊ P \mathcal{S} \models \Box \Diamond P
S ⊨ □ ◊ P
指定 P P P
S ⊨ ◊ □ P \mathcal{S} \models \Diamond \Box P
S ⊨ ◊ □ P
¬ □ ϕ ≡ ◊ ¬ ϕ ¬ ◊ ϕ ≡ □ ¬ ϕ ¬ ◯ ϕ ≡ ◯ ¬ ϕ \lnot\Box\phi\equiv\Diamond\lnot\phi \\ \lnot\Diamond\phi\equiv\Box\lnot\phi \\ \lnot\bigcirc\phi\equiv\bigcirc\lnot\phi
¬ □ ϕ ≡ ◊ ¬ ϕ ¬ ◊ ϕ ≡ □ ¬ ϕ ¬ ◯ ϕ ≡ ◯ ¬ ϕ
□ □ ϕ ≡ □ ϕ ◊ ◊ ϕ ≡ ◊ ϕ ϕ U ( ϕ U ψ ) ≡ ϕ U ψ ( ϕ U ψ ) U ψ ≡ ϕ U ψ \Box\Box\phi\equiv\Box\phi \\ \Diamond\Diamond\phi\equiv\Diamond\phi \\ \phi U(\phi U\psi)\equiv\phi U\psi \\ (\phi U\psi)U\psi\equiv\phi U\psi
□ □ ϕ ≡ □ ϕ ◊ ◊ ϕ ≡ ◊ ϕ ϕ U ( ϕ U ψ ) ≡ ϕ U ψ ( ϕ U ψ ) U ψ ≡ ϕ U ψ
◊ □ ◊ ϕ ≡ □ ◊ ϕ □ ◊ □ ϕ ≡ ◊ □ ϕ \Diamond\Box\Diamond\phi\equiv\Box\Diamond\phi \\ \Box\Diamond\Box\phi\equiv\Diamond\Box\phi
◊ □ ◊ ϕ ≡ □ ◊ ϕ □ ◊ □ ϕ ≡ ◊ □ ϕ
◯ ( ϕ U ψ ) ≡ ( ◯ ϕ ) U ( ◯ ψ ) ◊ ( ϕ ∨ ψ ) ≡ ( ◊ ϕ ) ∨ ( ◊ ψ ) □ ( ϕ ∧ ψ ) ≡ □ ϕ ∧ □ ψ \bigcirc(\phi U\psi)\equiv (\bigcirc\phi)U(\bigcirc\psi) \\ \Diamond(\phi \vee\psi)\equiv (\Diamond\phi)\vee(\Diamond\psi) \\ \Box(\phi\wedge\psi)\equiv\Box\phi\wedge\Box\psi
◯ ( ϕ U ψ ) ≡ ( ◯ ϕ ) U ( ◯ ψ ) ◊ ( ϕ ∨ ψ ) ≡ ( ◊ ϕ ) ∨ ( ◊ ψ ) □ ( ϕ ∧ ψ ) ≡ □ ϕ ∧ □ ψ
ϕ U ψ ≡ ψ ∨ ( ϕ ∧ ◯ ( ϕ U ψ ) ) ◊ ϕ ≡ ϕ ∨ ◯ ◊ ϕ □ ϕ ≡ ϕ ∧ ◯ □ ϕ \phi U\psi\equiv\psi\vee(\phi\wedge\bigcirc(\phi U\psi)) \\ \Diamond\phi\equiv\phi\vee\bigcirc\Diamond\phi \\ \Box\phi\equiv\phi\wedge\bigcirc\Box\phi
ϕ U ψ ≡ ψ ∨ ( ϕ ∧ ◯ ( ϕ U ψ ) ) ◊ ϕ ≡ ϕ ∨ ◯ ◊ ϕ □ ϕ ≡ ϕ ∧ ◯ □ ϕ
扩展率是非常重要的一条性质 ,之后的LTL模型检测都会基于此。
特别是这个第一条公式,我个人感觉其实它的意思就是基于当前项然后向后走了一步,就拿 ϕ U ψ \phi \mathcal{U}\psi ϕ U ψ ψ \psi ψ ϕ \phi ϕ
首先看扩展出来的第一个 ψ \psi ψ ψ \psi ψ
然后再看第二项 ϕ ∧ ◯ ( ϕ U ψ ) \phi\wedge\bigcirc(\phi U\psi) ϕ ∧ ◯ ( ϕ U ψ ) ϕ \phi ϕ ϕ U ψ \phi \mathcal{U}\psi ϕ U ψ
例如我们可以用它来表示两进程互斥问题中的公平性:
无条件的公平性:□ ◊ c r i t i \Box \Diamond crit_{i} □ ◊ c r i t i
强公平性:□ ◊ w a i t i → □ ◊ c r i t i \Box \Diamond wait_{i}\rightarrow \Box \Diamond crit_{i} □ ◊ w a i t i → □ ◊ c r i t i
弱公平性:◊ □ w a i t i → □ ◊ c r i t i \Diamond\Box wait_{i}\rightarrow \Box \Diamond crit_{i} ◊ □ w a i t i → □ ◊ c r i t i
前面介绍的until操作,它是一种比较强的限制,而weak until操作(或者称为unless)定义为:
ϕ W ψ = ( ϕ U ψ ) ∨ □ ϕ ϕ W ψ = ( ϕ U ψ ) ∨ □ ϕ \phi W\psi=(\phi U\psi)\vee\Box\phi
ϕWψ=(ϕUψ)∨□ϕ
ϕ W ψ = ( ϕ U ψ ) ∨ □ ϕ ϕ W ψ = ( ϕ U ψ ) ∨ □ ϕ
也就是说 ϕ W ψ \phi \mathcal{W} \psi ϕ W ψ ϕ U ψ \phi \mathcal{U} \psi ϕ U ψ □ ϕ \Box\phi □ ϕ
weak until和until操作是对偶的,具体表现为:
¬ ( ϕ U ψ ) = ( ϕ ∧ ¬ ψ ) W ( ¬ ϕ ∧ ¬ ψ ) ¬ ( ϕ W ψ ) = ( ϕ ∧ ¬ ψ ) U ( ¬ ϕ ∧ ¬ ψ ) \lnot(\phi \mathcal{U}\psi)=(\phi \wedge\lnot\psi)\mathcal{W}(\lnot\phi\wedge\lnot\psi) \\ \lnot(\phi \mathcal{W}\psi)=(\phi \wedge\lnot\psi)\mathcal{U}(\lnot\phi\wedge\lnot\psi)
¬ ( ϕ U ψ ) = ( ϕ ∧ ¬ ψ ) W ( ¬ ϕ ∧ ¬ ψ ) ¬ ( ϕ W ψ ) = ( ϕ ∧ ¬ ψ ) U ( ¬ ϕ ∧ ¬ ψ )
weak until和until两者的表达能力是相同的,两者之间可以互换
ϕ U ψ = ( ϕ W ψ ) ∧ ¬ □ ¬ ψ \phi \mathcal{U} \psi=(\phi \mathcal{W} \psi)\wedge\lnot\Box\lnot\psi
ϕ U ψ = ( ϕ W ψ ) ∧ ¬ □ ¬ ψ
也可以用它来表示一些其他属性:
◊ ψ \Diamond\psi
◊ ψ
ϕ U ψ \phi \mathcal{U} \psi
ϕ U ψ
□ ϕ \Box\phi
□ ϕ
□ ( ϕ ⇒ ◊ ψ ) \Box(\phi\Rightarrow\Diamond\psi)
□ ( ϕ ⇒ ◊ ψ )
指定系统(扮演服务器的角色)总是响应(Q)给定的请求(P):
S ⊨ □ ( P ⇒ ◊ Q ) \mathcal{S} \models \Box (P ⇒ \Diamond Q)
S ⊨ □ ( P ⇒ ◊ Q )
通常称为lead-to:
S ⊨ P ⇝ Q \mathcal{S} \models P \rightsquigarrow Q
S ⊨ P ⇝ Q
指定来自系统(扮演客户端的角色)的请求 P 只要没有有利的响应 Q 就稳定:
S ⊨ □ ( P ⇒ P W Q ) \mathcal{S} \models \Box (P ⇒ P \mathcal{W} Q)
S ⊨ □ ( P ⇒ P W Q )
两个进程不能同时进入临界区:
□ ( ¬ c r i t 1 ∨ ¬ c r i t 2 ) O R □ ( ∀ i , j ∈ 0.. N − 1 : s t a t e [ i ] = c r i t ∧ s t a t e [ j ] = c r i t ⇒ i = j ) \Box(\lnot crit_{1}\vee \lnot crit_{2}) \\
OR \qquad \Box(\forall i,j \in 0..N-1: state[i]=crit \;\land\;state[j]=crit \quad \Rightarrow \quad i=j )
□ ( ¬ c r i t 1 ∨ ¬ c r i t 2 ) O R □ ( ∀ i , j ∈ 0 . . N − 1 : s t a t e [ i ] = c r i t ∧ s t a t e [ j ] = c r i t ⇒ i = j )
两个进程可以无限经常次访问临界区:
( □ ◊ w 1 ⇒ □ ◊ c 1 ) ∧ ( □ ◊ w 2 ⇒ □ ◊ c 2 ) O R ∀ i ∈ 0.. N − 1 : s t a t e [ i ] = w a i t i n g ⇝ s t a t e [ i ] = c r i t (\Box\Diamond w_{1}\Rightarrow\Box\Diamond c_{1})\wedge(\Box\Diamond w_{2}\Rightarrow\Box\Diamond c_{2})\\
OR \qquad \forall i \in 0..N-1:state[i]=waiting \;\rightsquigarrow\; state[i]=crit
( □ ◊ w 1 ⇒ □ ◊ c 1 ) ∧ ( □ ◊ w 2 ⇒ □ ◊ c 2 ) O R ∀ i ∈ 0 . . N − 1 : s t a t e [ i ] = w a i t i n g ⇝ s t a t e [ i ] = c r i t
□ ( t r a i n _ i s _ n e a r → g a t e _ i s _ c l o s e ) \Box(train\_is\_near\rightarrow gate\_is\_close)
□ ( t r a i n _ i s _ n e a r → g a t e _ i s _ c l o s e )
□ ( r e q u e s t → ◊ r e s p o n s e ) \Box(request\rightarrow \Diamond response)
□ ( r e q u e s t → ◊ r e s p o n s e )
T L A + TLA^+ T L A + T L A + TLA+ T L A + T L A + TLA+ T L A +
带有 □ \Box □ ◊ \Diamond ◊ ⇝ \rightsquigarrow ⇝ ∀ ∀ ∀ ∃ ∃ ∃
没有 U \mathcal{U} U W \mathcal{W} W
□ ( p ⇒ ( p W q ) ) = □ ( p ⇒ ( p ′ ∨ q ) ) \Box (p ⇒ (p \mathcal{W}q)) = \Box (p ⇒ (p' \lor q)) □ ( p ⇒ ( p W q ) ) = □ ( p ⇒ ( p ′ ∨ q ) ) □ ( p ⇒ ( p U q ) ) = □ ( p ⇒ ( p ′ ∨ q ) ) ∧ □ ( p ⇒ ◊ q ) \Box (p ⇒ (p \mathcal{U}q)) = \Box (p ⇒ (p' \lor q)) \land \Box(p ⇒ \Diamond q) □ ( p ⇒ ( p U q ) ) = □ ( p ⇒ ( p ′ ∨ q ) ) ∧ □ ( p ⇒ ◊ q )
E N A B L E A _{ENABLE} \mathcal{A} E N A B L E A s s s A \mathcal{A} A s s s
W F e ( A ) ≜ □ ◊ ¬ ( E N A B L E ⟨ A ⟩ e ) ∨ □ ◊ ⟨ A ⟩ e \mathcal{WF}_e(\mathcal{A}) \triangleq \Box \Diamond \neg (_{ENABLE} ⟨\mathcal{A}⟩_e) \lor \Box \Diamond ⟨\mathcal{A}⟩_e W F e ( A ) ≜ □ ◊ ¬ ( E N A B L E ⟨ A ⟩ e ) ∨ □ ◊ ⟨ A ⟩ e
如果 A \mathcal{A} A
S F e ( A ) ≜ ◊ □ ¬ ( E N A B L E ⟨ A ⟩ e ) ∨ □ ◊ ⟨ A ⟩ e \mathcal{SF}_e(\mathcal{A}) \triangleq \Diamond \Box \neg (_{ENABLE} ⟨\mathcal{A}⟩_e) \lor \Box \Diamond ⟨\mathcal{A}⟩_e S F e ( A ) ≜ ◊ □ ¬ ( E N A B L E ⟨ A ⟩ e ) ∨ □ ◊ ⟨ A ⟩ e
如果 A 是无限频繁可触发的,它将被触发。
通常,TLA+ 规范是一系列谓词的连词(conjonction):
I ∧ □ [ N ] v ∧ E \mathcal{I} \land \Box [\mathcal{N}]_v \land \mathcal{E}
I ∧ □ [ N ] v ∧ E
I \mathcal{I} I N \mathcal{N} N E \mathcal{E} E W F v ( A 1 ) ∧ W F v ( A 3 ) ∧ . . . \mathcal{WF}_v(\mathcal{A}_1) \land \mathcal{WF}_v(\mathcal{A}_3) \land ... W F v ( A 1 ) ∧ W F v ( A 3 ) ∧ . . .
如果 P c ⇒ P a P_c ⇒ P_a P c ⇒ P a P c P_c P c P a P_a P a P c P_c P c P a P_a P a
这意味着如果 P a ⊨ P P_a \models P P a ⊨ P P c ⊨ P P_c \models P P c ⊨ P
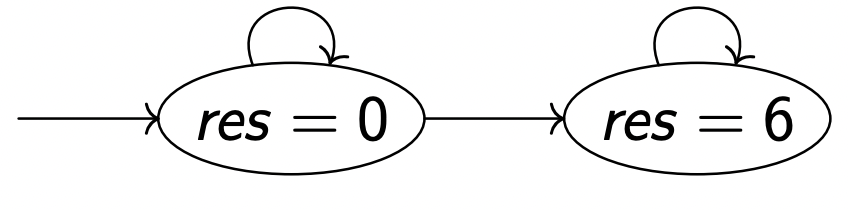
1 2 3 4 5 6 7 8 9 -----------------module somme1---------------- EXTENDS Naturals CONSTANT N VARIABLE res TypeInvariant == res \in Nat Init == res = 0 Next == res′ = ((N + 1) * N) / 2 Spec == Init ∧ [][Next]_res /\ WF_res (Next)
当 N = 3 N = 3 N = 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ----------------- module somme2 ---------------- EXTENDS Naturals CONSTANT N VARIABLE res, acc, disp TypeInvariant == res \in Nat /\ acc \in Nat /\ disp \in SUBSET 1..N Init == res = 0 /\ acc = 0 /\ disp = 1..N Next == \/ \E i \in disp : acc' = acc + i /\ disp' = disp \ {i} /\ UNCHANGED res \/ disp = {} /\ res' = acc /\ UNCHANGED res Spec == Init ∧ [][Next]_<<res, disp, acc>> /\ WF_<<res, disp, acc>> (Next)
当 N = 3 N = 3 N = 3

分解:引入中间转换
1 2 3 4 5 ---------------- module somme2_raffine_somme1 ---------------- EXTENDS somme2 Orig == INSTANCE somme1 Raffinement == Orig ! Spec THEOREM Spec => Orig ! Spec
1 2 3 4 5 6 7 8 9 10 11 12 13 14 ----------------- module somme3 ---------------- EXTENDS Naturals CONSTANT N VARIABLE res, acc, i TypeInvariant == res \in Nat /\ acc \in Nat /\ i \in 1..N Init == res = 0 /\ acc = 0 /\ i = N Next == \/ i > 0 /\ acc' = acc + i /\ i' = i - 1 /\ UNCHANGED res \/ i = 0 /\ res' = acc /\ UNCHANGED <<i, res>> Spec == Init ∧ [][Next]_<<res, i, acc>> /\ WF_<<res, i, acc>> (Next)
当 N = 3 N = 3 N = 3
减少非确定性 + 表示变化(数据细化) d i s p = 1.. i disp = 1..i d i s p = 1 . . i
1 2 3 4 5 6 ---------------- module somme3_raffine_somme2 ---------------- EXTENDS somme3 dispMapping == 1..i Orig == INSTANCE somme2 WITH disp <- dispMapping Raffinement == Orig ! Spec THEOREM Spec => Orig ! Spec
F 在 命 题 逻 辑 中 可 证 明 □ F S T L 1 \frac{F 在命题逻辑中可证明}{\Box F} \;STL1
□ F F 在 命 题 逻 辑 中 可 证 明 S T L 1
意义:
□ F ⇒ F S T L 2 \frac{}{\Box F ⇒ F} \;STL2
□ F ⇒ F S T L 2
□ □ F = □ G S T L 3 \frac{}{\Box \Box F = \Box G} \;STL3
□ □ F = □ G S T L 3
F ⇒ G □ F ⇒ □ G S T L 4 \frac{F ⇒ G}{\Box F ⇒ \Box G} \;STL4
□ F ⇒ □ G F ⇒ G S T L 4
□ ( F ∧ G ) = ( □ F ) ∧ ( □ G ) S T L 5 \frac{}{\Box (F \land G) = (\Box F) \land (\Box G)} \;STL5
□ ( F ∧ G ) = ( □ F ) ∧ ( □ G ) S T L 5
( ◊ □ F ) ∧ ( ◊ □ G ) = ◊ □ ( F ∧ G ) S T L 6 \frac{}{ (\Diamond \Box F) \land (\Diamond \Box G) = \Diamond \Box (F \land G)} \;STL6
( ◊ □ F ) ∧ ( ◊ □ G ) = ◊ □ ( F ∧ G ) S T L 6
P ∧ ( v ′ = v ) ⇒ P ′ □ P = P ∧ □ [ P ⇒ P ′ ] v T L A 1 \frac{P \land (v' = v) ⇒ P'}{\Box P = P \land \Box [P ⇒ P']_v} \;TLA1
□ P = P ∧ □ [ P ⇒ P ′ ] v P ∧ ( v ′ = v ) ⇒ P ′ T L A 1
P ∧ [ A ] v 1 ⇒ Q ∧ [ B ] v 2 □ P ∧ □ [ A ] v 1 ⇒ □ Q ∧ □ [ B ] v 2 T L A 2 \frac{P \land [\mathcal{A}]_{v1} ⇒ Q \land [\mathcal{B}]_{v2}}{\Box P \land \Box [\mathcal{A}]_{v1} ⇒ \Box Q \land \Box[\mathcal{B}]_{v2}} \;TLA2
□ P ∧ □ [ A ] v 1 ⇒ □ Q ∧ □ [ B ] v 2 P ∧ [ A ] v 1 ⇒ Q ∧ [ B ] v 2 T L A 2
I ∧ [ N ] v ⇒ I ′ I ∧ □ [ N ] v ⇒ □ I I N V 1 \frac{I \land [\mathcal{N}]_{v} ⇒ I'}{I \land \Box[\mathcal{N}]_{v} ⇒ \Box I} \;INV1
I ∧ □ [ N ] v ⇒ □ I I ∧ [ N ] v ⇒ I ′ I N V 1
□ I ⇒ ( □ [ N ] v = □ [ N ∧ I ∧ I ′ ] v ) I N V 2 \frac{}{\Box I ⇒ (\Box[\mathcal{N}]_{v} = \Box [\mathcal{N} \land I \land I']_v)} \;INV2
□ I ⇒ ( □ [ N ] v = □ [ N ∧ I ∧ I ′ ] v ) I N V 2
P ∧ [ N ] v ⇒ ( P ′ ∨ Q ′ ) P ∧ ⟨ N ∧ A ⟩ v ⇒ Q ′ P ⇒ E N A B L E ⟨ A ⟩ v □ [ N ] v ) ∧ W F v ( A ) ⇒ ( P ⇝ Q ) W F 1 \frac{\begin{aligned} P \land [\mathcal{N}]_v ⇒ (P' \lor Q') \\ P \land ⟨\mathcal{N} \land \mathcal{A}⟩_v ⇒ Q' \\ P ⇒ _{ENABLE} ⟨\mathcal{A}⟩_v\end{aligned}}{\Box [\mathcal{N}]_v) \land WF_v(\mathcal{A}) ⇒ (P \rightsquigarrow Q)} \;WF1
□ [ N ] v ) ∧ W F v ( A ) ⇒ ( P ⇝ Q ) P ∧ [ N ] v ⇒ ( P ′ ∨ Q ′ ) P ∧ ⟨ N ∧ A ⟩ v ⇒ Q ′ P ⇒ E N A B L E ⟨ A ⟩ v W F 1
P ∧ [ N ] v ⇒ ( P ′ ∨ Q ′ ) P ∧ ⟨ N ∧ A ⟩ v ⇒ Q ′ □ P ∧ □ [ N ] v ∧ □ F ⇒ ◊ E N A B L E ⟨ A ⟩ v □ [ N ] v ) ∧ S F v ( A ) ∧ □ F ⇒ ( P ⇝ Q ) W F 1 \frac{\begin{aligned} P \land [\mathcal{N}]_v ⇒ (P' \lor Q') \\ P \land ⟨\mathcal{N} \land \mathcal{A}⟩_v ⇒ Q' \\ \Box P \land \Box [\mathcal{N}]_v \land \Box F ⇒ \Diamond _{ENABLE} ⟨\mathcal{A}⟩_v\end{aligned}}{\Box [\mathcal{N}]_v) \land SF_v(\mathcal{A}) \land \Box F ⇒ (P \rightsquigarrow Q)} \;WF1
□ [ N ] v ) ∧ S F v ( A ) ∧ □ F ⇒ ( P ⇝ Q ) P ∧ [ N ] v ⇒ ( P ′ ∨ Q ′ ) P ∧ ⟨ N ∧ A ⟩ v ⇒ Q ′ □ P ∧ □ [ N ] v ∧ □ F ⇒ ◊ E N A B L E ⟨ A ⟩ v W F 1
□ ( P ⇒ □ P ) ∧ ◊ P ◊ □ P L D S T B L \frac{\Box(P ⇒ \Box P) \land \Diamond P}{\Diamond \Box P} \;LDSTBL
◊ □ P □ ( P ⇒ □ P ) ∧ ◊ P L D S T B L
P ⇝ Q ∧ Q ⇝ R P ⇝ R T R A N S \frac{P \rightsquigarrow Q \land Q \rightsquigarrow R}{P \rightsquigarrow R} \;TRANS
P ⇝ R P ⇝ Q ∧ Q ⇝ R T R A N S
∀ m ∈ W : P ( m ) ⇝ Q ( ∃ m ∈ W : P ( m ) ) ⇝ Q I N F D I J \frac{\forall m \in W : P(m) \rightsquigarrow Q}{(∃ m \in W : P(m)) \rightsquigarrow Q} \;INFDIJ
( ∃ m ∈ W : P ( m ) ) ⇝ Q ∀ m ∈ W : P ( m ) ⇝ Q I N F D I J
原则:构建执行图并研究属性。
□ P \Box P □ P P P P □ P ( v , v ′ ) \Box P (v,v') □ P ( v , v ′ ) P ( v , v ′ ) P(v,v') P ( v , v ′ ) 活跃度 ◊ P \Diamond P ◊ P P ⇝ Q P \rightsquigarrow Q P ⇝ Q
让系统 S = ⟨ S , I , R ⟩ \mathcal{S} = ⟨S, I, R⟩ S = ⟨ S , I , R ⟩ ∣ S ∣ |S| ∣ S ∣ F \mathcal{F} F ∣ F ∣ |F| ∣ F ∣
验证 S ⊨ F \mathcal{S} \models \mathcal{F} S ⊨ F
O ( ∣ S ∣ × 2 ∣ F ∣ ) O(|S| × 2^{|F|})
O ( ∣ S ∣ × 2 ∣ F ∣ )
TLC 模型检查器可以检查:
带有保护的动作的规约;
没有初始变量的不变量 □ P \Box P □ P
带有素变量(prime variables )和重复(begaiement)的纯安全公式 □ [ P ] v \Box [P]_v □ [ P ] v
P ⇝ Q P \rightsquigarrow Q P ⇝ Q
将 □ \Box □
注意:系统和公式的状态空间必须是有限的:例如任何有界量化。
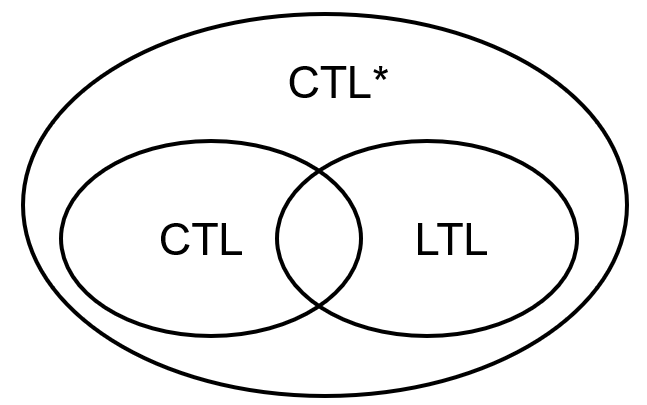
C T L CTL C T L 在前面我们已经介绍了线性属性,为了方便地去描述这个线性属性,我们又介绍了线性时序逻辑,本节要介绍一种新的逻辑计算树逻辑(CTL),这种逻辑可以描述LTL不能描述的部分。
如果用文氏图来表示的话就是:
让我们先来回想一下LTL之所以称为线性的,是因为时间的定性概念是基于路径 的,并且被视为线性的 :在每个时刻只有唯一的一个可能的后继状态,因此每个时刻都有一个唯一的可能的未来。 从技术上讲,这是基于以下事实:LTL公式的解释是根据路径(即状态序列)定义的 。
但是路径本身可能存在着分支 ,例如在一个TS系统中,一个状态也许有着多个后继状态,从这个角度来看这种解释是基于状态分支的。我们想到,某些时候在一个状态的所有可能计算都满足某个条件,或者有些时候一个状态的部分可能计算满足某个条件,为了表述这些个性质,我们加入∀ \forall ∀ ∃ ∃ ∃
LTL描述的从某个状态开始所有的路径情况,例如s ⊨ □ ( x ≤ 20 ) s \models \Box(x\le 20) s ⊨ □ ( x ≤ 2 0 ) x ≤ 20 x\le 20 x ≤ 2 0
而CTL描述的是从某个状态开始的所有或部分路径情况
例如s ⊨ ∀ □ ( x ≤ 20 ) s\models \forall\Box(x\le 20) s ⊨ ∀ □ ( x ≤ 2 0 ) x ≤ 20 x\le 20 x ≤ 2 0 s ⊨ ∃ □ ( x ≤ 20 ) s\models∃\Box(x\le 20) s ⊨ ∃ □ ( x ≤ 2 0 ) x ≤ 20 x\le 20 x ≤ 2 0
linear time
branching time
行为behavior
path-based:trace(s)
state-based:computation tree of s
时间逻辑temporal logic
LTL path formulas
CTL state formulas
模型检测
P S P A C E − c o m p l e t e O ( s i z e ( T S ) ⋅ 2 ∣ ϕ ∣ ) PSPACE-complete O(size(TS)·2^{\mid\phi\mid}) P S P A C E − c o m p l e t e O ( s i z e ( T S ) ⋅ 2 ∣ ϕ ∣ ) P T I M E O ( s i z e ( T S ) ⋅ ∣ ϕ ∣ ) PTIME O(size(TS)·\mid\phi\mid) P T I M E O ( s i z e ( T S ) ⋅ ∣ ϕ ∣ )
公平性
可以直接表示
需要额外的技术
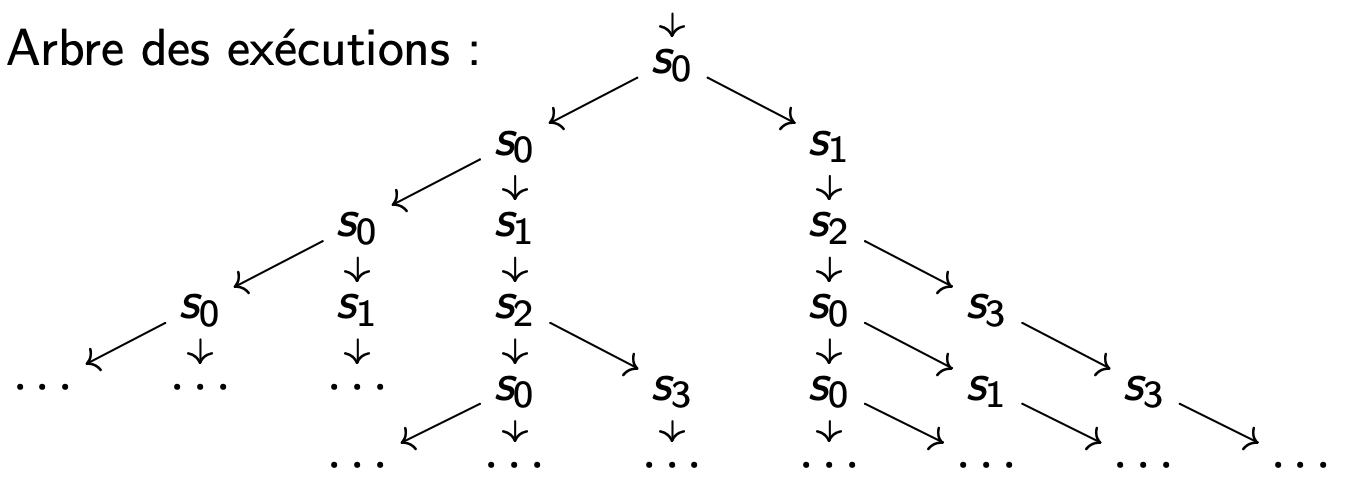
执行集:E x e c ( S ) = ⟨ ( s 0 + → s 1 → s 2 ) ∗ → s 0 ω ⟩ , ⟨ ( s 0 + → s 1 → s 2 ) ω ⟩ , ⟨ ( s 0 + → s 1 → s 2 ) + → s 3 ω ⟩ Exec(S) = ⟨({s_0}^+ → s_1 → s_2)^∗ → {s_0}^ω⟩,⟨({s_0}^+ → s_1 → s_2)^ω⟩,⟨({s_0}^+ → s_1 → s_2)^+ → s_3^ω⟩ E x e c ( S ) = ⟨ ( s 0 + → s 1 → s 2 ) ∗ → s 0 ω ⟩ , ⟨ ( s 0 + → s 1 → s 2 ) ω ⟩ , ⟨ ( s 0 + → s 1 → s 2 ) + → s 3 ω ⟩
执行树:
CTL 公式始终与系统的给定状态 s 相关,迹 Trace(s) 源自该状态。S 的状态构成了这个逻辑的模型。
与 LTL 的区别(从句法上讲)在于迹量词的时间运算符的出现。
当且仅当 a ∈ L ( s ) a∈L_(s) a ∈ L ( s )
s ⊨ a \frac{}{s \models a}
s ⊨ a
s ⊨ P ∧ Q s\models P \land Q s ⊨ P ∧ Q 当且仅当 s ⊨ P s\models P s ⊨ P s ⊨ Q s\models Q s ⊨ Q
s ⊨ P s ⊨ Q s ⊨ P ∧ Q \frac{s \models P \qquad s \models Q}{s \models P \land Q}
s ⊨ P ∧ Q s ⊨ P s ⊨ Q
s ⊨ P ∨ Q s \models P \lor Q s ⊨ P ∨ Q 当且仅当 s ⊨ P s \models P s ⊨ P s ⊨ Q s \models Q s ⊨ Q
s ⊨ P s ⊨ P ∨ Q s ⊨ Q s ⊨ P ∨ Q \frac{s \models P}{s \models P \lor Q} \qquad
\frac{s \models Q}{s \models P \lor Q}
s ⊨ P ∨ Q s ⊨ P s ⊨ P ∨ Q s ⊨ Q
s ⊭ ¬ P s\nvDash \neg P s ⊭ ¬ P 当且仅当 $ s\models P$
s ⊨ P s ⊭ ¬ P \frac{s \models P}{s \nvDash \neg P}
s ⊭ ¬ P s ⊨ P
s ⊨ ∃ φ s\models ∃ φ s ⊨ ∃ φ 当且仅当 π ⊨ ϕ \pi\vDash\phi π ⊨ ϕ 某些 从s开始的路径成立
s ⊨ ∀ φ s\models \forall φ s ⊨ ∀ φ 当且仅当 π ⊨ ϕ \pi\vDash\phi π ⊨ ϕ 所有 从s开始的路径成立
π ⊨ ◯ P \pi\vDash\bigcirc P π ⊨ ◯ P π [ 1 ] = P \pi[1]=P π [ 1 ] = P π ⊨ P U Q \pi\vDash P \mathcal{U} Q π ⊨ P U Q 存在 j ≥ 0 j\ge0 j ≥ 0 s j ⊨ Q s_{j}\vDash Q s j ⊨ Q 0 ≤ k < j , π [ k ] ⊨ P 0\le k\lt j,\pi[k]\vDash P 0 ≤ k < j , π [ k ] ⊨ P
对于一个CTL公式 ϕ \phi ϕ S a t ( ϕ ) Sat(\phi) S a t ( ϕ )
S a t ( ϕ ) = { s ∈ S ∣ s ⊨ ϕ } Sat(\phi)=\{s\in S | s\vDash \phi\}
S a t ( ϕ ) = { s ∈ S ∣ s ⊨ ϕ }
说白了就是一些满足CTL公式ϕ \phi ϕ
如果我们说一个TS满足CTL公式 ϕ \phi ϕ ϕ \phi ϕ
T S ⊨ ϕ 当且仅当 S 0 ⊆ S a t ( ϕ ) 当且仅当 ∀ s 0 ∈ S 0 . s 0 ⊨ ϕ TS\vDash\phi\text{ 当且仅当 }S_{0}\subseteq Sat(\phi) \text{ 当且仅当 }\forall s_{0}\in S_{0}.s_{0}\vDash\phi
T S ⊨ ϕ 当且仅当 S 0 ⊆ S a t ( ϕ ) 当且仅当 ∀ s 0 ∈ S 0 . s 0 ⊨ ϕ
上面的 S 0 S_{0} S 0
提醒:对于迹 σ \sigma σ σ i \sigma_i σ i σ \sigma σ
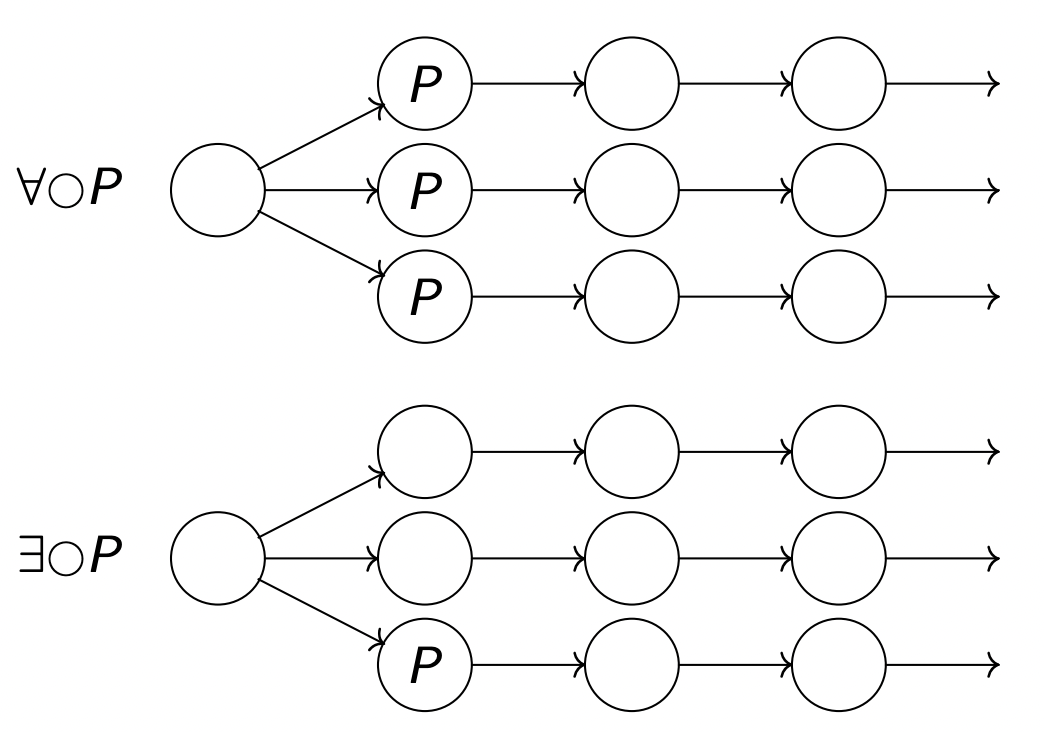
s ⊨ ∀ ◯ P s \models \forall \bigcirc P s ⊨ ∀ ◯ P P 在下一瞬间为真
∀ σ ∈ T r a c e s ( S ) : a 1 ⊨ P s ⊨ ∀ ◯ P \frac{\forall \sigma \in Traces(S) :a_1 \models P}{s \models \forall \bigcirc P}
s ⊨ ∀ ◯ P ∀ σ ∈ T r a c e s ( S ) : a 1 ⊨ P
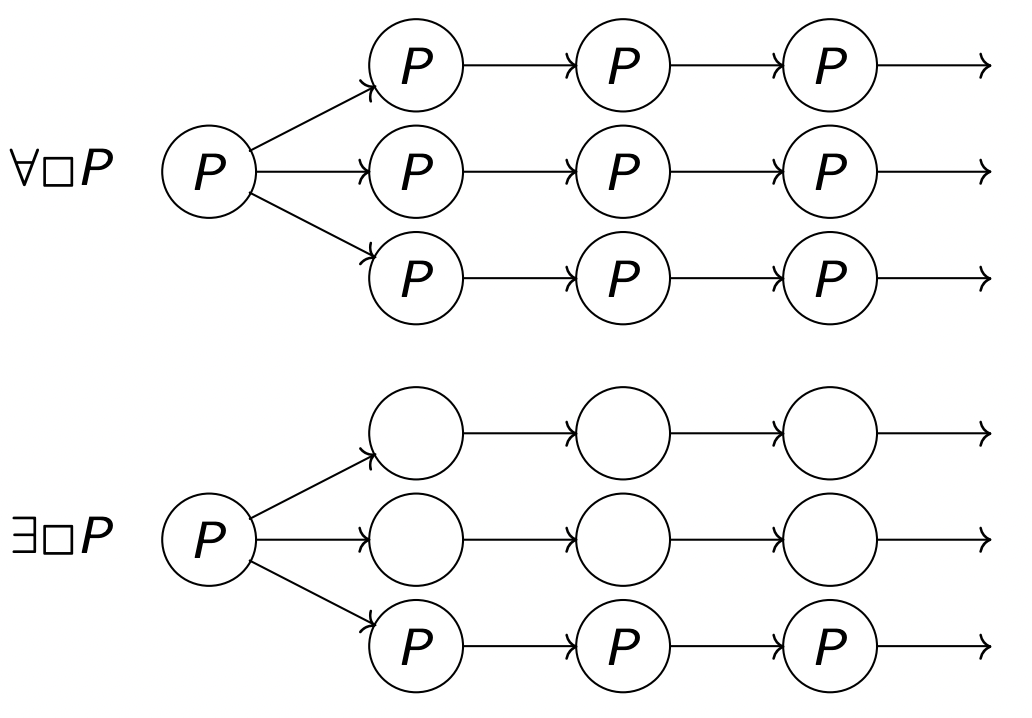
s ⊨ ∀ □ P s \models \forall \Box P s ⊨ ∀ □ P P 在每个状态下始终为真
∀ σ ∈ T r a c e s ( S ) : ∀ i ≥ 0 : a i ⊨ P s ⊨ ∀ □ P \frac{\forall \sigma \in Traces(S) : \forall i \ge 0 :a_i \models P}{s \models \forall \Box P}
s ⊨ ∀ □ P ∀ σ ∈ T r a c e s ( S ) : ∀ i ≥ 0 : a i ⊨ P
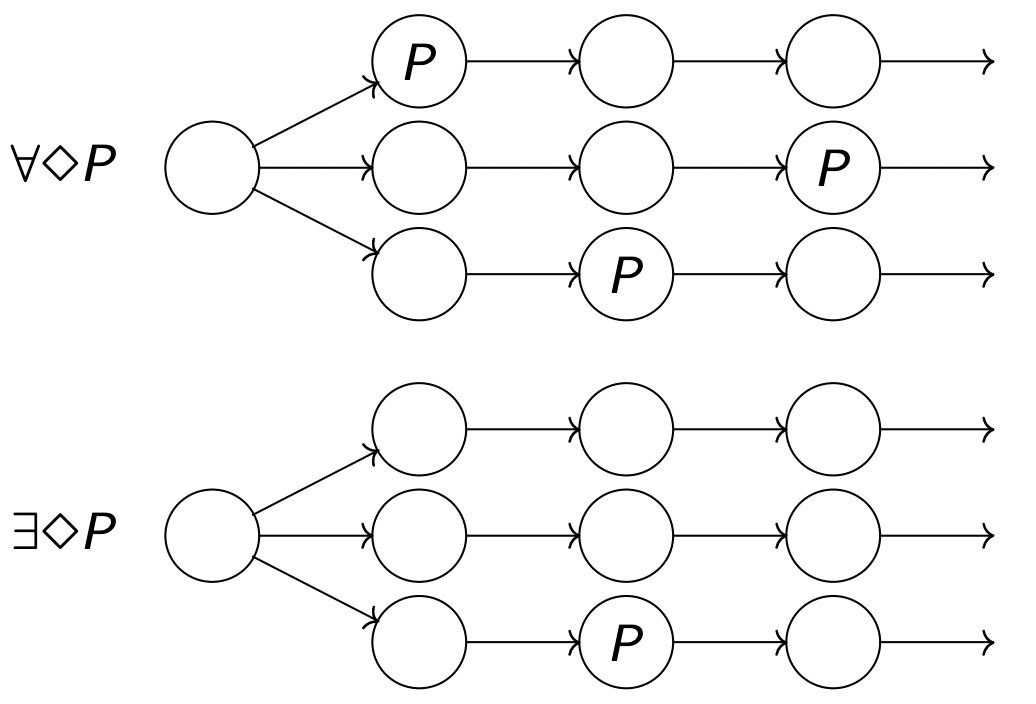
s ⊨ ∀ ◊ P s \models \forall \Diamond P s ⊨ ∀ ◊ P P 最终为真(未来)
∀ σ ∈ T r a c e s ( S ) : ∃ i ≥ 0 : a i ⊨ P s ⊨ ∀ ◊ P \frac{\forall \sigma \in Traces(S) : ∃ i \ge 0 :a_i \models P}{s \models \forall \Diamond P}
s ⊨ ∀ ◊ P ∀ σ ∈ T r a c e s ( S ) : ∃ i ≥ 0 : a i ⊨ P
s ⊨ P ∀ U Q s \models P\;\forall\;\mathcal{U}\;Q s ⊨ P ∀ U Q P 最终为真,同时 P 仍然为真
∀ σ ∈ T r a c e s ( S ) : ∃ j ≥ 0 : a j ⊨ Q ∧ ∀ i < j : σ i ⊨ P s ⊨ P ∀ U Q \frac{\forall \sigma \in Traces(S) : ∃ j \ge 0 :a_j \models Q \land \forall i < j : \sigma_i \models P}{s \models P\;\forall\;\mathcal{U}\;Q}
s ⊨ P ∀ U Q ∀ σ ∈ T r a c e s ( S ) : ∃ j ≥ 0 : a j ⊨ Q ∧ ∀ i < j : σ i ⊨ P
s ⊨ ∃ ◯ P s \models ∃ \bigcirc P s ⊨ ∃ ◯ P P 在下一瞬间为真
∃ σ ∈ T r a c e s ( S ) : a 1 ⊨ P s ⊨ ∃ ◯ P \frac{∃ \sigma \in Traces(S) :a_1 \models P}{s \models ∃ \bigcirc P}
s ⊨ ∃ ◯ P ∃ σ ∈ T r a c e s ( S ) : a 1 ⊨ P
s ⊨ ∃ □ P s \models ∃ \Box P s ⊨ ∃ □ P P 在每个状态下始终为真
∃ σ ∈ T r a c e s ( S ) : ∀ i ≥ 0 : a i ⊨ P s ⊨ ∃ □ P \frac{∃ \sigma \in Traces(S) : \forall i \ge 0 :a_i \models P}{s \models ∃ \Box P}
s ⊨ ∃ □ P ∃ σ ∈ T r a c e s ( S ) : ∀ i ≥ 0 : a i ⊨ P
s ⊨ ∃ ◊ P s \models ∃ \Diamond P s ⊨ ∃ ◊ P P 最终为真(未来)
∃ σ ∈ T r a c e s ( S ) : ∃ i ≥ 0 : a i ⊨ P s ⊨ ∃ ◊ P \frac{∃ \sigma \in Traces(S) : ∃ i \ge 0 :a_i \models P}{s \models ∃ \Diamond P}
s ⊨ ∃ ◊ P ∃ σ ∈ T r a c e s ( S ) : ∃ i ≥ 0 : a i ⊨ P
s ⊨ P ∃ U Q s \models P\;∃\;\mathcal{U}\;Q s ⊨ P ∃ U Q Q 最终为真,同时 P 仍然为真
∃ σ ∈ T r a c e s ( S ) : ∃ j ≥ 0 : a j ⊨ Q ∧ ∀ i < j : σ i ⊨ P s ⊨ P ∃ U Q \frac{∃ \sigma \in Traces(S) : ∃ j \ge 0 :a_j \models Q \land \forall i < j : \sigma_i \models P}{s \models P\;∃\;\mathcal{U}\;Q}
s ⊨ P ∃ U Q ∃ σ ∈ T r a c e s ( S ) : ∃ j ≥ 0 : a j ⊨ Q ∧ ∀ i < j : σ i ⊨ P
∀ ◯ \forall \bigcirc ∀ ◯ ∃ ◯ ∃ \bigcirc ∃ ◯ ∀ □ \forall \Box ∀ □ ∃ □ ∃ \Box ∃ □ ∀ ◊ \forall \Diamond ∀ ◊ ∃ ◊ ∃ \Diamond ∃ ◊ ∀ U \forall \mathcal{U} ∀ U ∃ U ∃ \mathcal{U} ∃ U
{ ∀ ◯ , ∀ U , ∃ U } ∨ { ∃ ◯ , ∃ □ , ∃ U } ∨ { ∃ ⋄ , ∃ U , ∃ ◯ } \{ \forall \bigcirc , \forall \mathcal{U}, ∃ \mathcal{U}\} \lor \{ ∃ \bigcirc , ∃ \Box, ∃ \mathcal{U}\} \lor \{ ∃ \diamond , ∃ \mathcal{U}, ∃ \bigcirc \} { ∀ ◯ , ∀ U , ∃ U } ∨ { ∃ ◯ , ∃ □ , ∃ U } ∨ { ∃ ⋄ , ∃ U , ∃ ◯ }
∃ ◯ P ≜ ¬ ∀ ¬ P ∃ \bigcirc P \triangleq \neg \forall \neg P ∃ ◯ P ≜ ¬ ∀ ¬ P ∀ ◊ P ≜ T r u e ∀ U P \forall \Diamond P \triangleq True \; \forall \mathcal{U} P ∀ ◊ P ≜ T r u e ∀ U P ∃ ◊ P ≜ T r u e ∃ U P ∃ \Diamond P \triangleq True \; ∃ \mathcal{U} P ∃ ◊ P ≜ T r u e ∃ U P ∀ □ P ≜ ¬ ∃ ◊ ¬ P \forall \Box P \triangleq \neg ∃ \Diamond \neg P ∀ □ P ≜ ¬ ∃ ◊ ¬ P ∃ □ P ≜ ¬ ∀ ◊ ¬ P ∃ \Box P \triangleq \neg \forall \Diamond \neg P ∃ □ P ≜ ¬ ∀ ◊ ¬ P
∀ ↔ A ∀ ↔ A ∀ ↔ A ∃ ↔ E ∃ ↔ E ∃ ↔ E □ ↔ G \Box ↔ G □ ↔ G ◊ ↔ F \Diamond ↔ F ◊ ↔ F ◯ ↔ X \bigcirc ↔ X ◯ ↔ X U ↔ U \mathcal{U} ↔ U U ↔ U
P ∃ W Q ≜ ∃ □ P ∨ P ∃ U Q P∃ \mathcal{W}Q \triangleq ∃ \Box P \lor P ∃ \mathcal{U} Q P ∃ W Q ≜ ∃ □ P ∨ P ∃ U Q $P\forall \mathcal{W}Q $ 不等于 $ \forall \Box P \lor P \forall \mathcal{U} Q; ; ;
与 LTL 不同,对于任何 CTL 属性,我们有:
S ⊨ F , 或 S ⊨ ¬ F , 或 S ⊭ F ≡ S ⊨ ¬ F 。 S \models F,或\; S \models \neg F,
或\; S \nvDash F ≡ S \models ¬F。
S ⊨ F , 或 S ⊨ ¬ F , 或 S ⊭ F ≡ S ⊨ ¬ F 。
公式的否定$ ∀, ∃, \Box, \Diamond$
对基于 $ ∀, ∃, \Box, \Diamond$ 的公式的求反只需将每个运算符反转为对偶即可。
例:
¬ ( ∀ ◊ ∃ □ p ) = ∃ □ ∀ ◊ ¬ p ¬(∀ \Diamond ∃ \Box p) = ∃\Box ∀\Diamond ¬p ¬ ( ∀ ◊ ∃ □ p ) = ∃ □ ∀ ◊ ¬ p
( ∀ ◊ ¬ s 0 ⇒ ∀ ◊ s 3 ) = ( ∃ □ s 0 ∨ ∀ ◊ s 3 ) 因 为 ( p ⇒ q ) = ( ¬ p ∨ q ) (∀\Diamond ¬s_0 ⇒ ∀\Diamond s_3) = (∃\Box s_0 ∨ ∀\Diamond s_3) \qquad 因为 (p ⇒ q) = (¬p ∨ q) ( ∀ ◊ ¬ s 0 ⇒ ∀ ◊ s 3 ) = ( ∃ □ s 0 ∨ ∀ ◊ s 3 ) 因 为 ( p ⇒ q ) = ( ¬ p ∨ q )
一旦定义了 ∃ ◯ ∃\bigcirc ∃ ◯ ∀ ◯ ∀\bigcirc ∀ ◯
其归纳定义:
∀ □ f = f ∧ ∀ ◯ ∀ □ f ∀ \Box f = f ∧ ∀ \bigcirc ∀ \Box f ∀ □ f = f ∧ ∀ ◯ ∀ □ f
∃ □ f = f ∧ ∃ ◯ ∃ □ f ∃ \Box f = f ∧ ∃ \bigcirc ∃ \Box f ∃ □ f = f ∧ ∃ ◯ ∃ □ f
∀ ◊ f = f ∨ ∀ ◯ ∀ ◊ □ f ∀ \Diamond f = f ∨ ∀ \bigcirc ∀ \Diamond \Box f ∀ ◊ f = f ∨ ∀ ◯ ∀ ◊ □ f
∃ ◊ f = f ∨ ∃ ◯ ∃ ◊ □ f ∃ \Diamond f = f ∨ ∃ \bigcirc ∃ \Diamond \Box f ∃ ◊ f = f ∨ ∃ ◯ ∃ ◊ □ f
f ∀ U g = g ∨ ( f ∧ ∀ ◯ ( f ∀ U g ) ) f ∀ \mathcal{U} g = g ∨ (f ∧ ∀\bigcirc (f ∀ \mathcal{U} g)) f ∀ U g = g ∨ ( f ∧ ∀ ◯ ( f ∀ U g ) )
f ∃ U g = g ∨ ( f ∧ ∃ ◯ ( f ∃ U g ) ) f ∃ \mathcal{U} g = g ∨ (f ∧ ∃\bigcirc (f ∃ \mathcal{U} g)) f ∃ U g = g ∨ ( f ∧ ∃ ◯ ( f ∃ U g ) )
(对于实现模型检查器特别有用)
L T L v s C T L LTL \; vs \; CTL L T L v s C T L 由之前的一张图我们看到,CTL和LTL有部分的表达是有交集的,这部分既可以用LTL表达,又可以用CTL表达,那么如何形式化地定义等价这个概念呢?
如果一个LTL公式 φ φ φ Φ \Phi Φ φ ≡ Φ φ\equiv\Phi φ ≡ Φ
T S ⊨ φ ⇔ T S ⊨ Φ TS\vDash φ\Leftrightarrow TS\vDash\Phi
T S ⊨ φ ⇔ T S ⊨ Φ
例如有这些个公式是等价的
CTL公式 Φ \Phi Φ
LTL公式 φ φ φ
a a a a a a
$ \forall\bigcirc a$
◯ a \bigcirc a ◯ a
∀ ( a U b ) \forall(a\mathcal{U}b) ∀ ( a U b ) a U b a\mathcal{U}b a U b
∀ □ a \forall\Box a ∀ □ a □ a \Box a □ a
∀ ◊ a \forall\Diamond a ∀ ◊ a ◊ a \Diamond a ◊ a
∀ ( a W b ) \forall(a\mathcal{W}b) ∀ ( a W b ) a W b a\mathcal{W}b a W b
∀ □ ∀ ◊ a \forall\Box\forall\Diamond a ∀ □ ∀ ◊ a □ ◊ a \Box\Diamond a □ ◊ a
由上面的文氏图我们知道,LTL和CTL的表达能力并不完全等价,因为存在着只要有各自能够表达的部分
某些LTL公式不能表示成CTL公式,例如
◊ □ a \Diamond\Box a ◊ □ a ◊ ( a ∧ ◯ a ) \Diamond(a\land\bigcirc a) ◊ ( a ∧ ◯ a )
某些CTL公式不能表示成LTL公式,例如
∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀ ◊ ∀ □ a $ \forall\Diamond(a\land\forall\bigcirc a)$
∀ □ ∃ ◊ a \forall\Box\exist\Diamond a ∀ □ ∃ ◊ a
◊ ( a ∧ ◯ a ) \Diamond(a\wedge\bigcirc a) ◊ ( a ∧ ◯ a )
例如下面这张图:
我们可以看到它能表示LTL公式 $ \Diamond(a\land\bigcirc a), 但 是 不 能 表 示 C T L 公 式 ,但是不能表示CTL公式 , 但 是 不 能 表 示 C T L 公 式 S 0 , S 3 S_{0},S_{3} S 0 , S 3 ∀ ◊ ( a ∧ ∀ ◯ a ) \forall\Diamond(a\wedge\forall\bigcirc a) ∀ ◊ ( a ∧ ∀ ◯ a ) S 0 S_{0} S 0 a a a
再看另一个例子,◊ □ a \Diamond\Box a ◊ □ a ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀ ◊ ∀ □ a
就如下图所示
它能够表示LTL公式 ◊ □ a \Diamond\Box a ◊ □ a ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀ ◊ ∀ □ a
我们看到最左边的那条路径,也就是说如果走的路径为 S 0 S 0 S 0 S 0 S 0 S 0 . . . S_{0}S_{0}S_{0}S_{0}S_{0}S_{0}... S 0 S 0 S 0 S 0 S 0 S 0 . . . ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀ ◊ ∀ □ a
LTL模型检测的时间复杂度为
O ( ∣ T S ∣ ⋅ 2 ∣ ϕ ∣ ) O(|TS|·2^{|\phi|})
O ( ∣ T S ∣ ⋅ 2 ∣ ϕ ∣ )
CTL模型检测的时间复杂度为
O ( ∣ T S ∣ ⋅ ∣ ϕ ∣ ) O(|TS|·|\phi|)
O ( ∣ T S ∣ ⋅ ∣ ϕ ∣ )
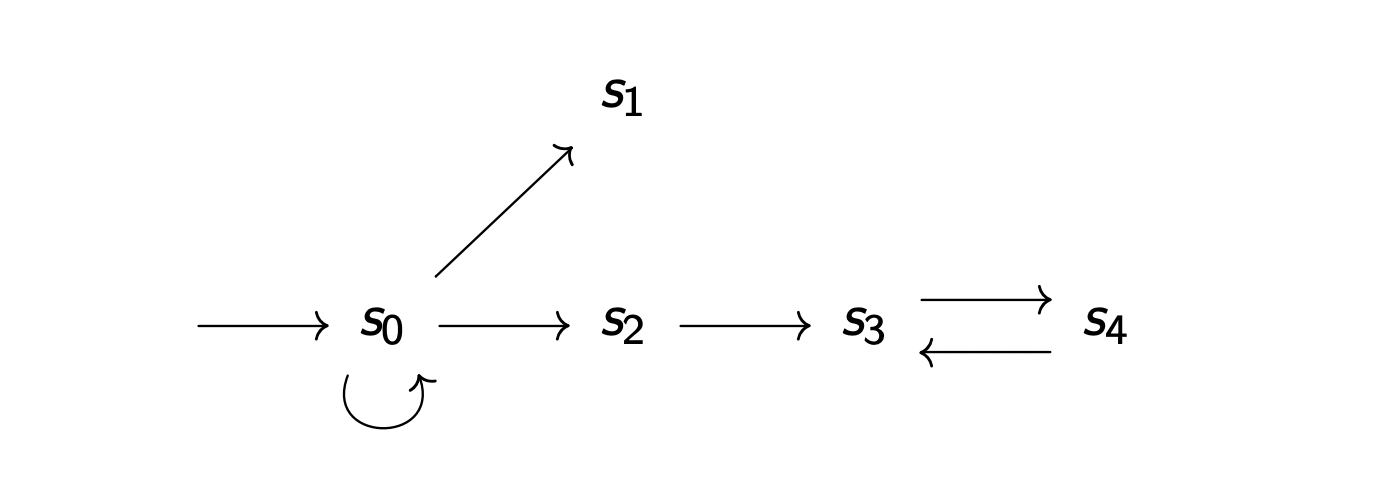
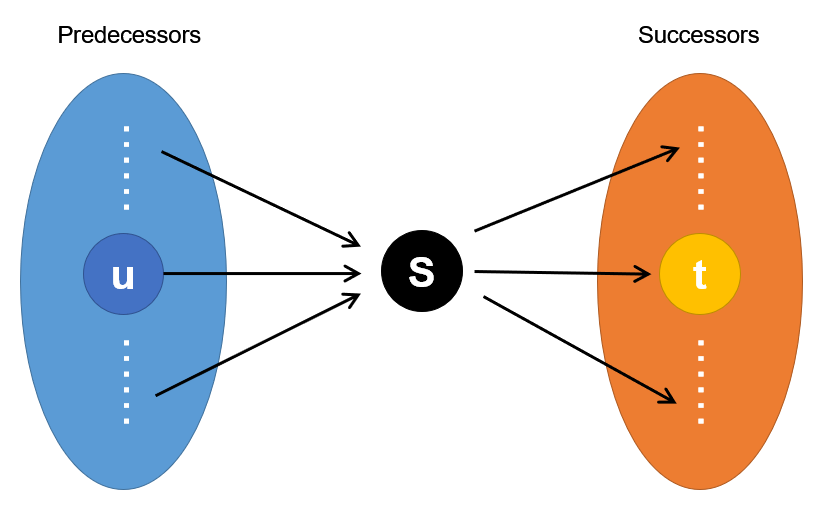

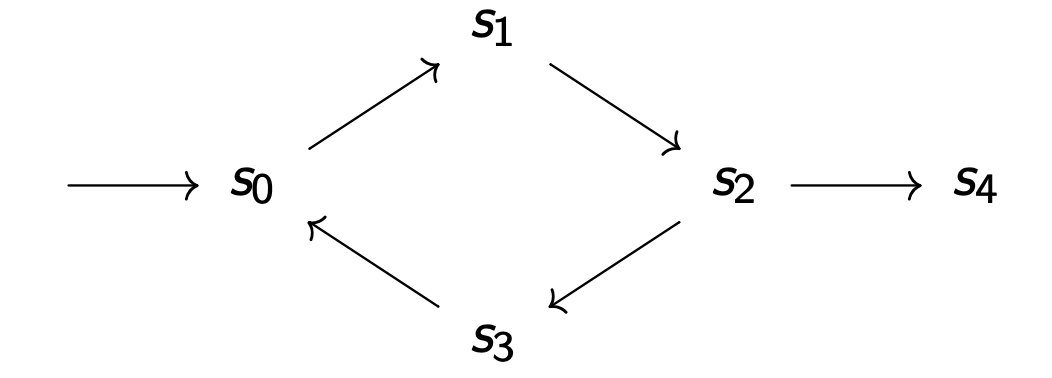
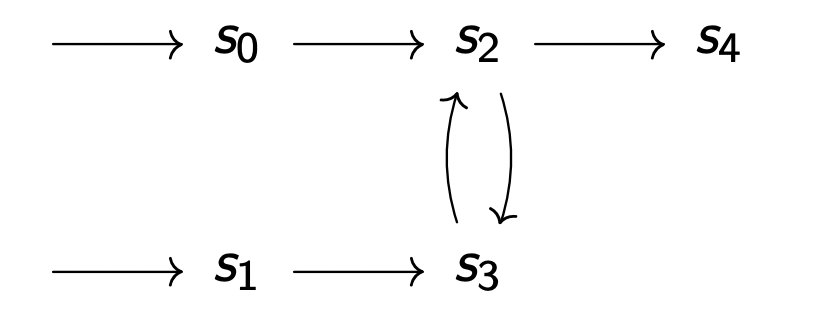
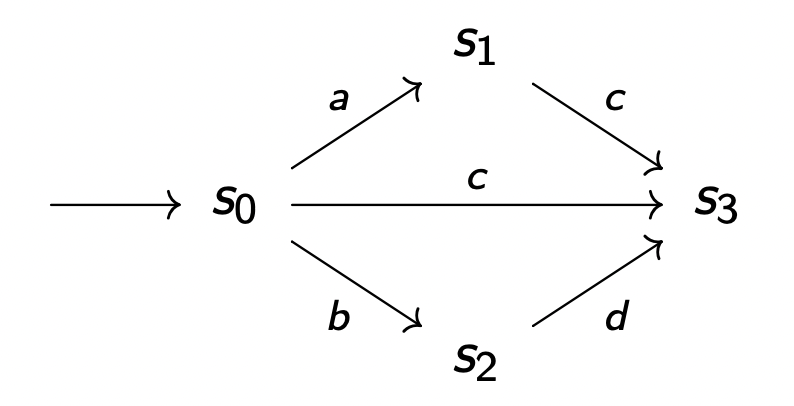
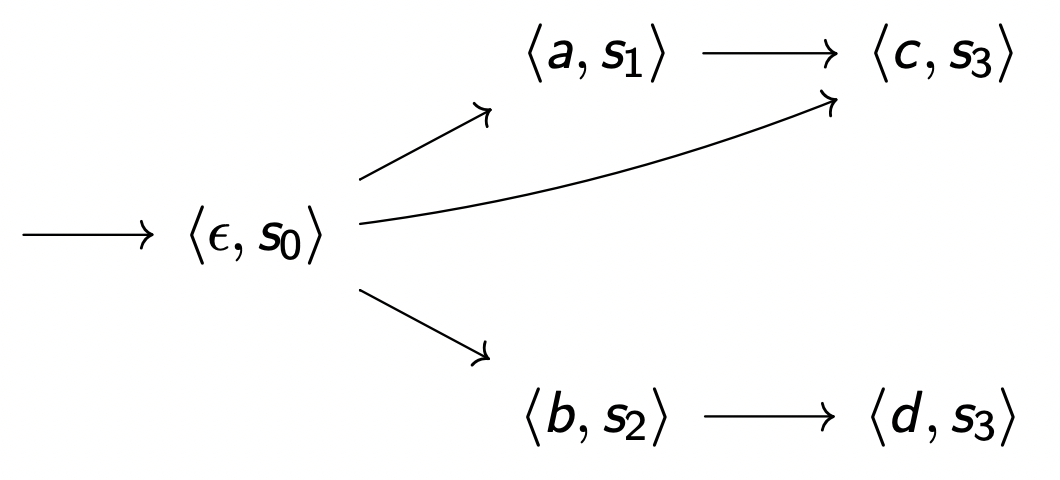
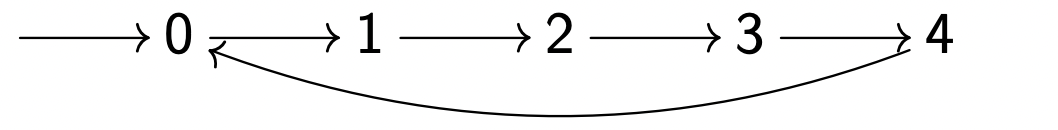
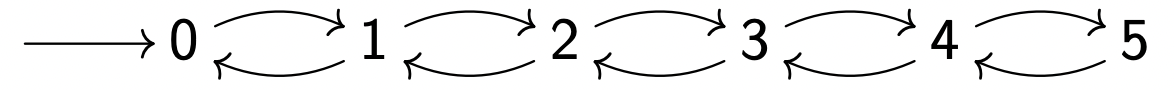
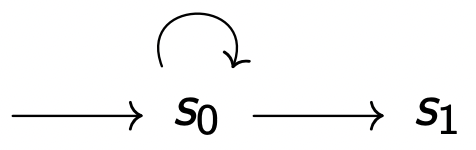
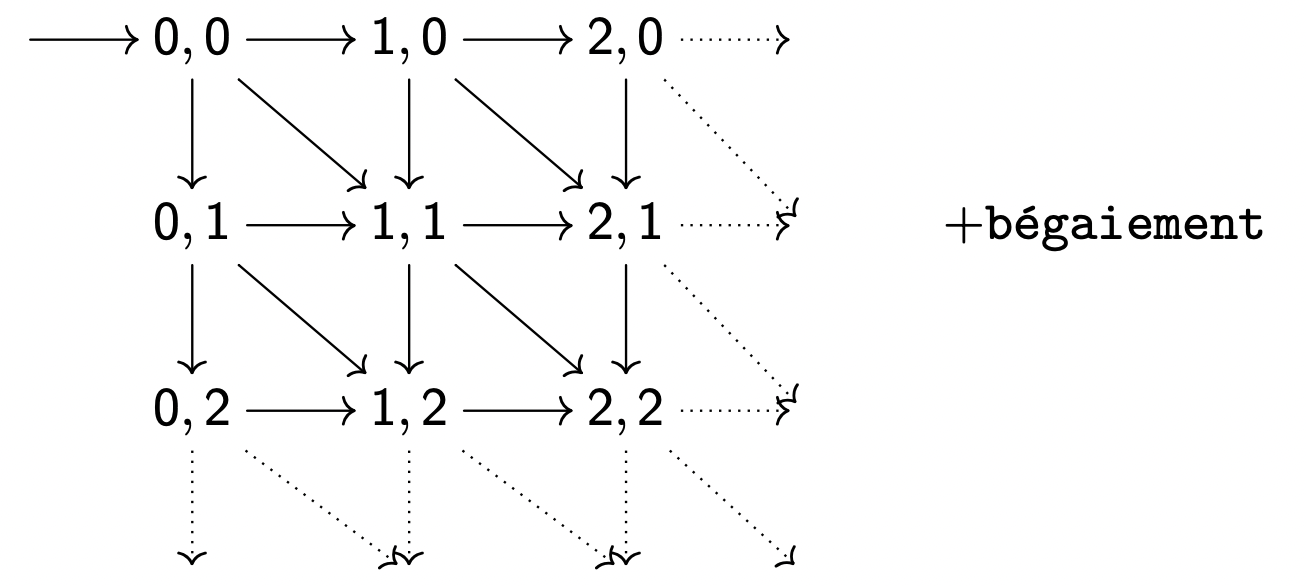
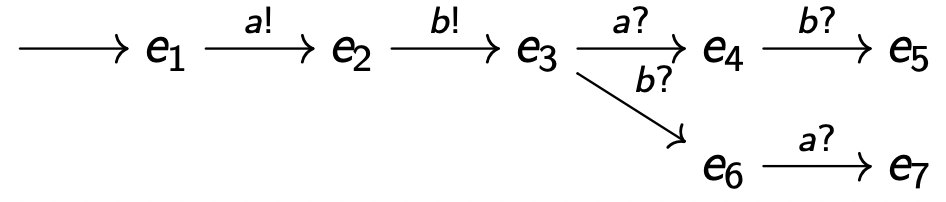
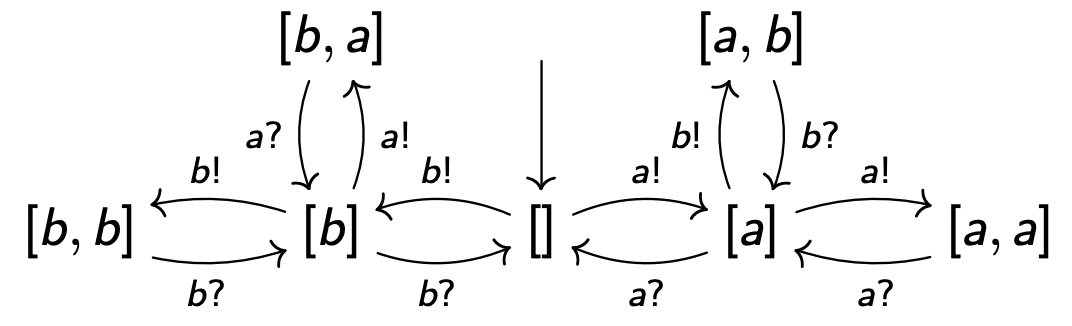
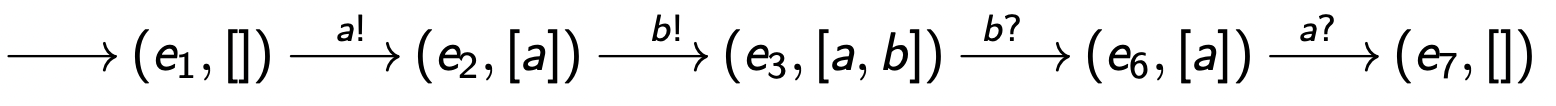
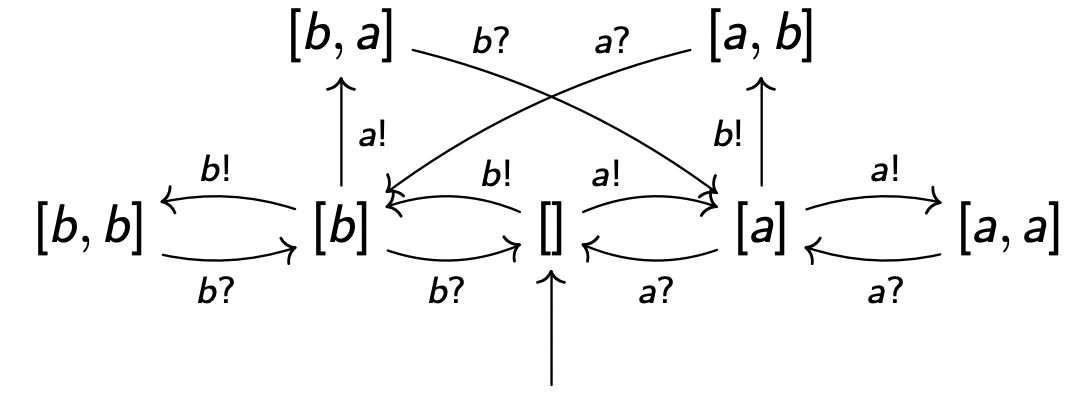
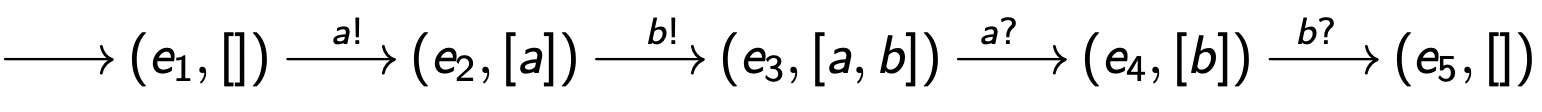
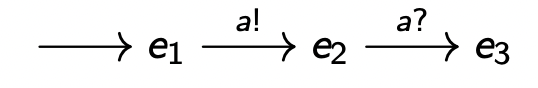
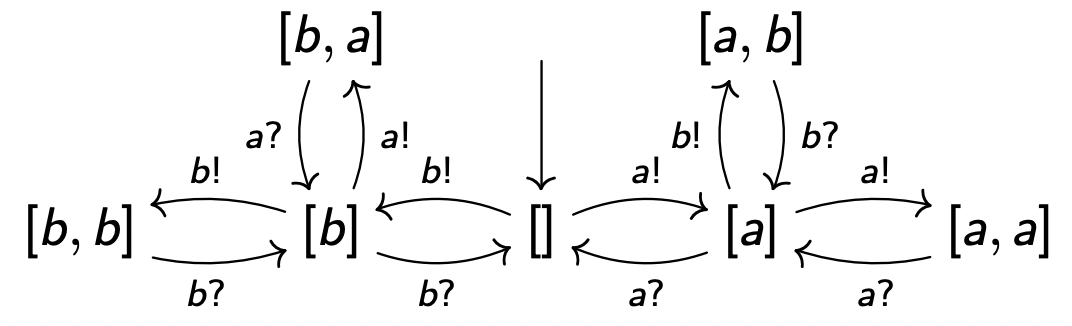
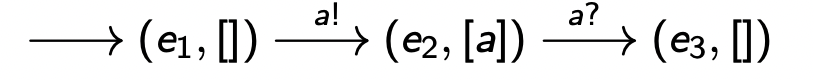
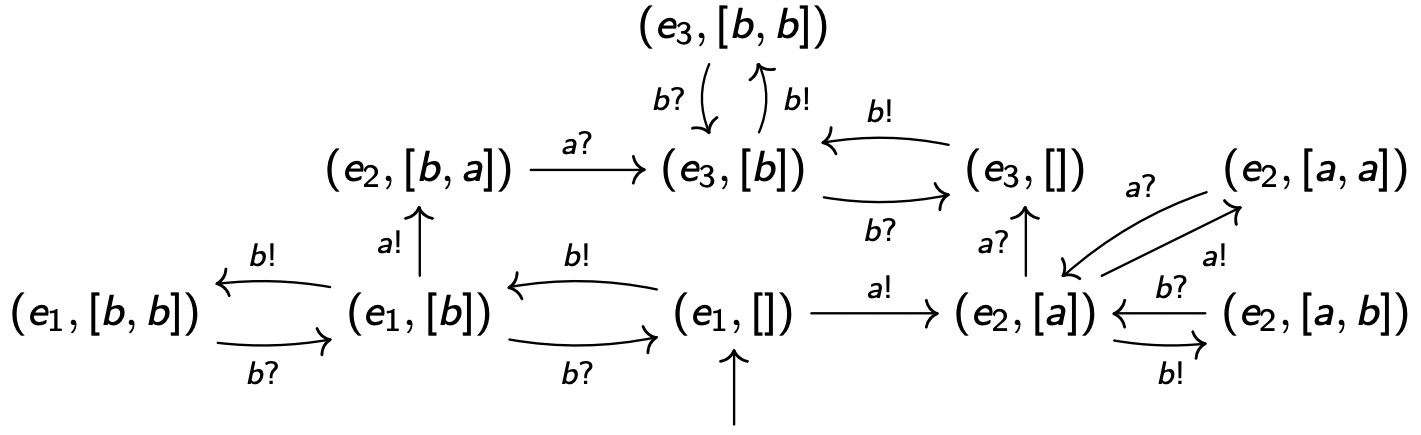

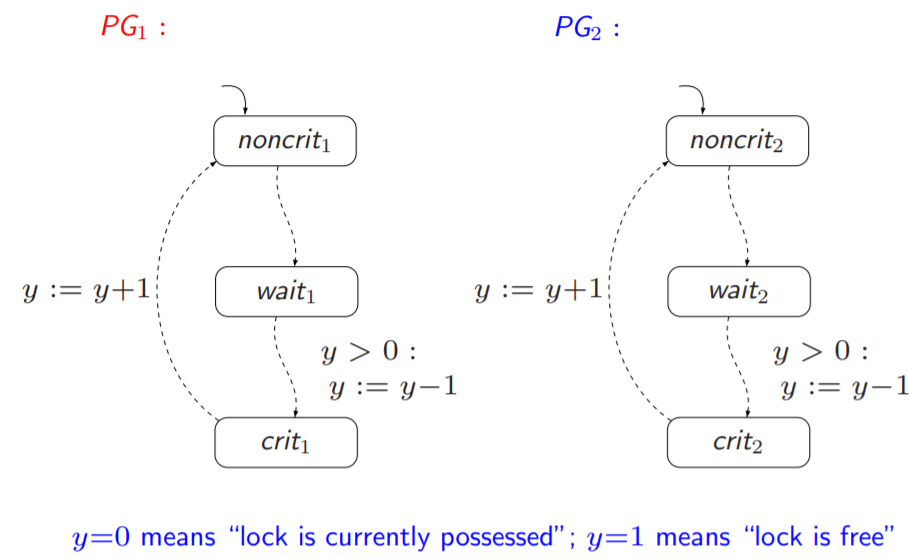
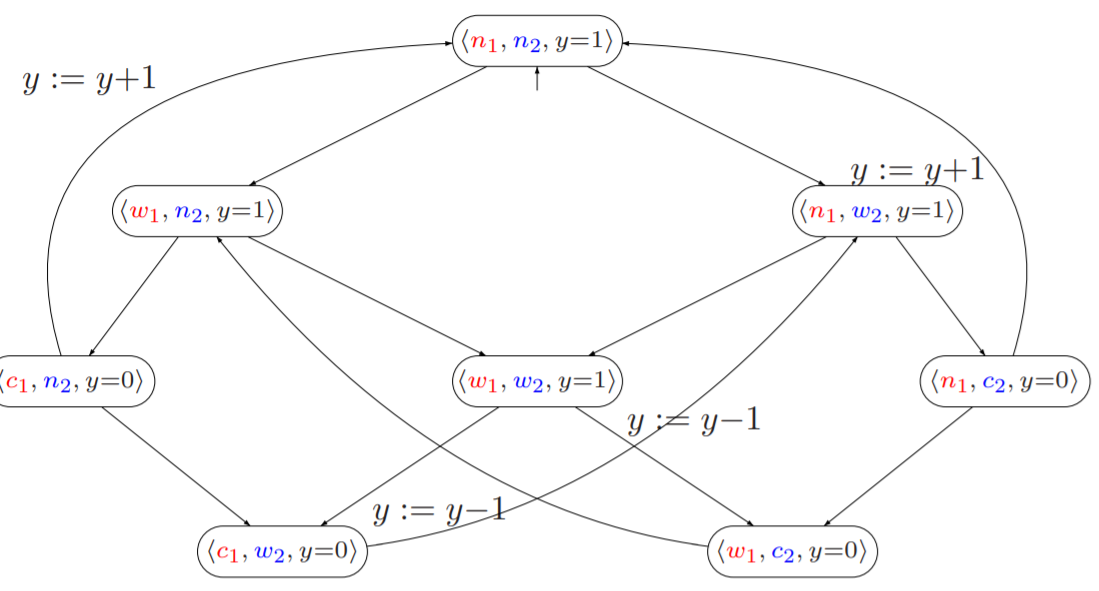
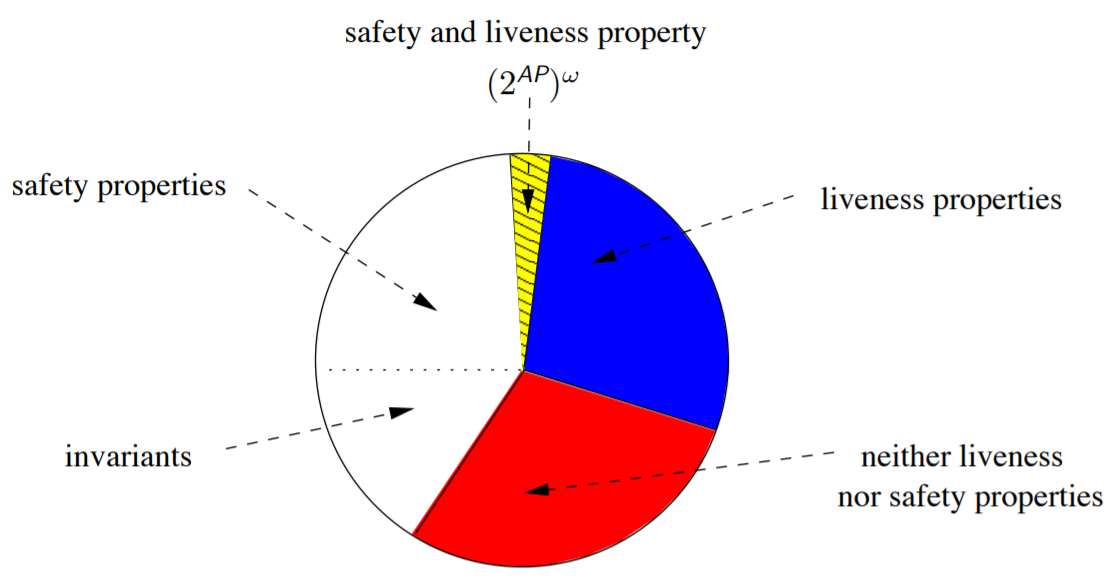
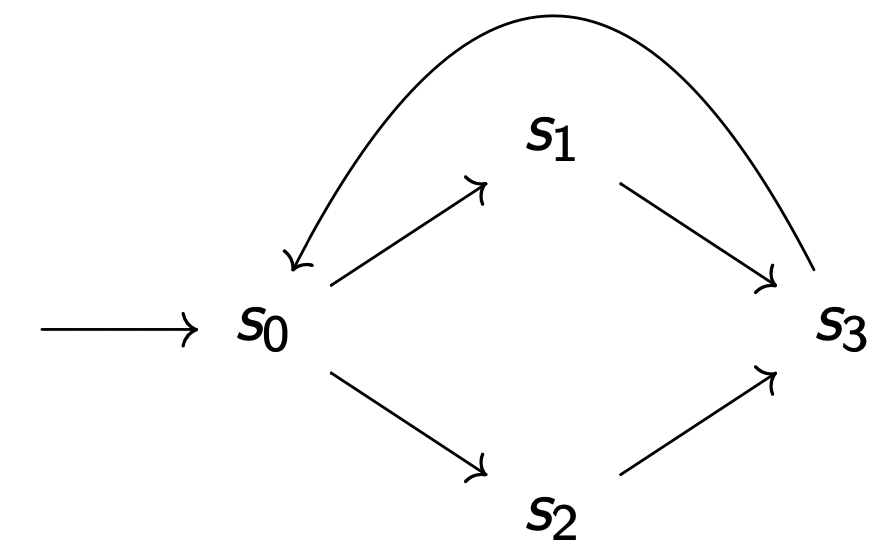
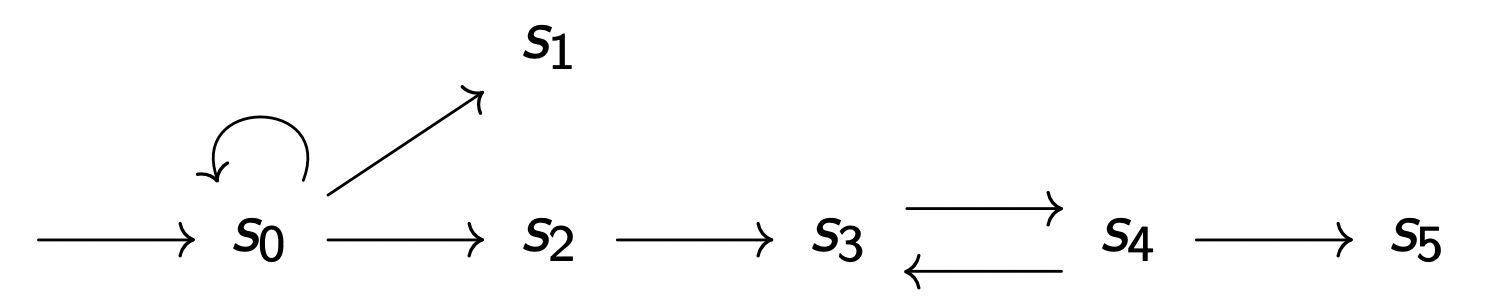
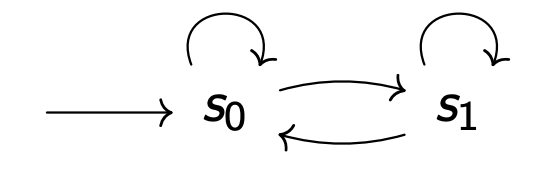
 与下述带有简单公平性的ST系统等价:
与下述带有简单公平性的ST系统等价: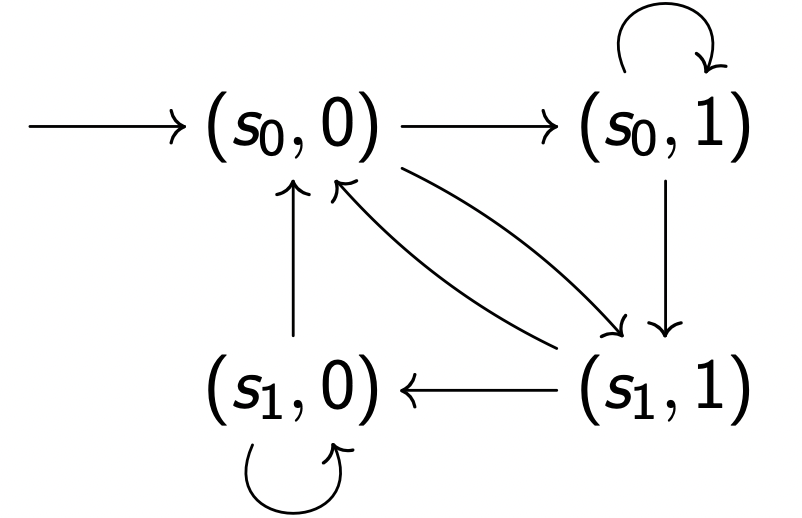
 与下述带有简单公平性,的ST系统等价:
与下述带有简单公平性,的ST系统等价: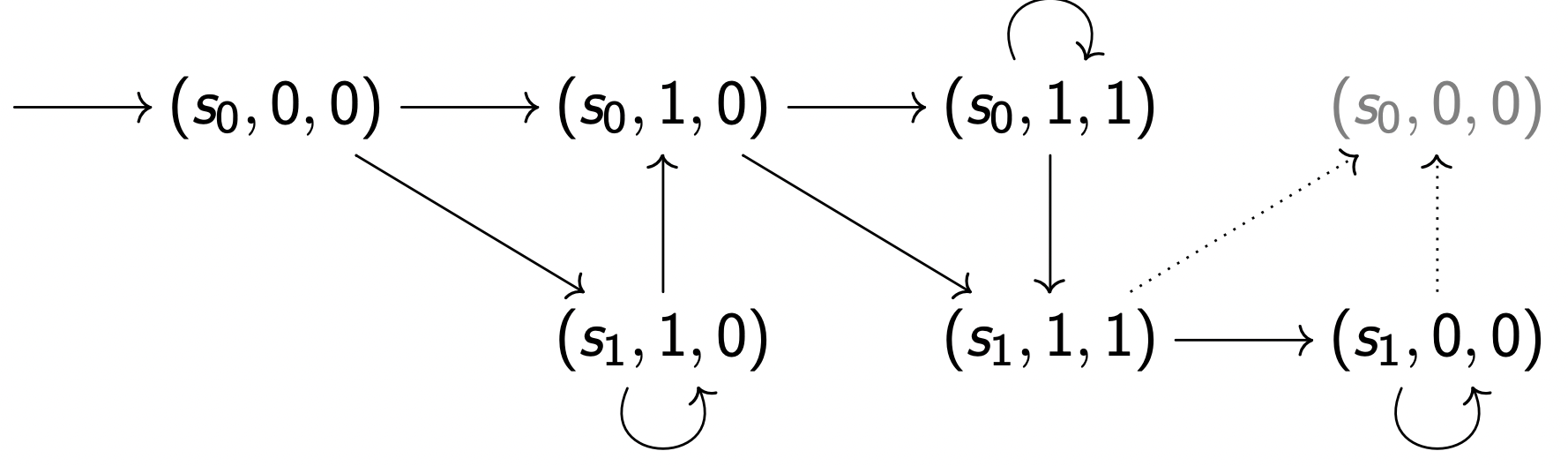

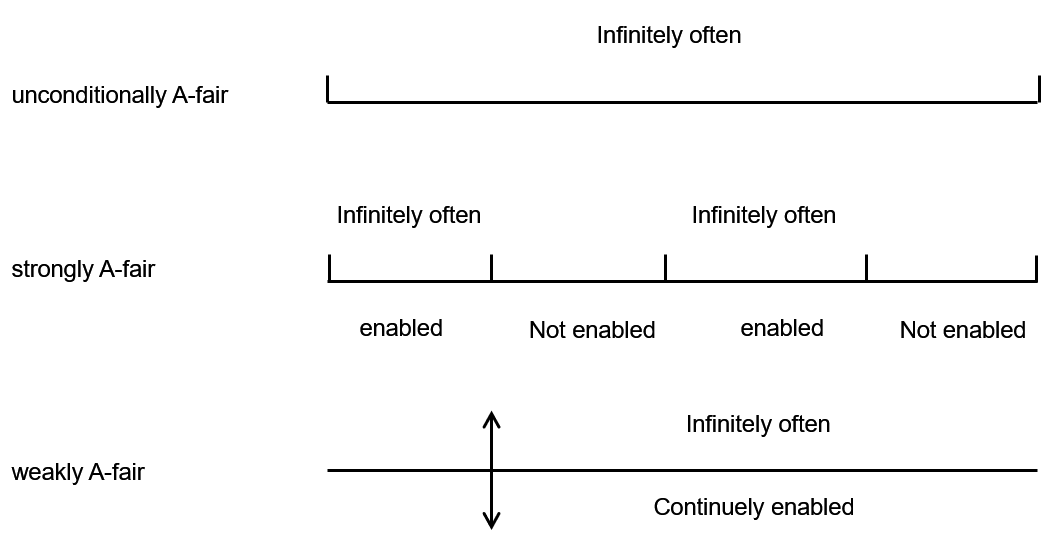
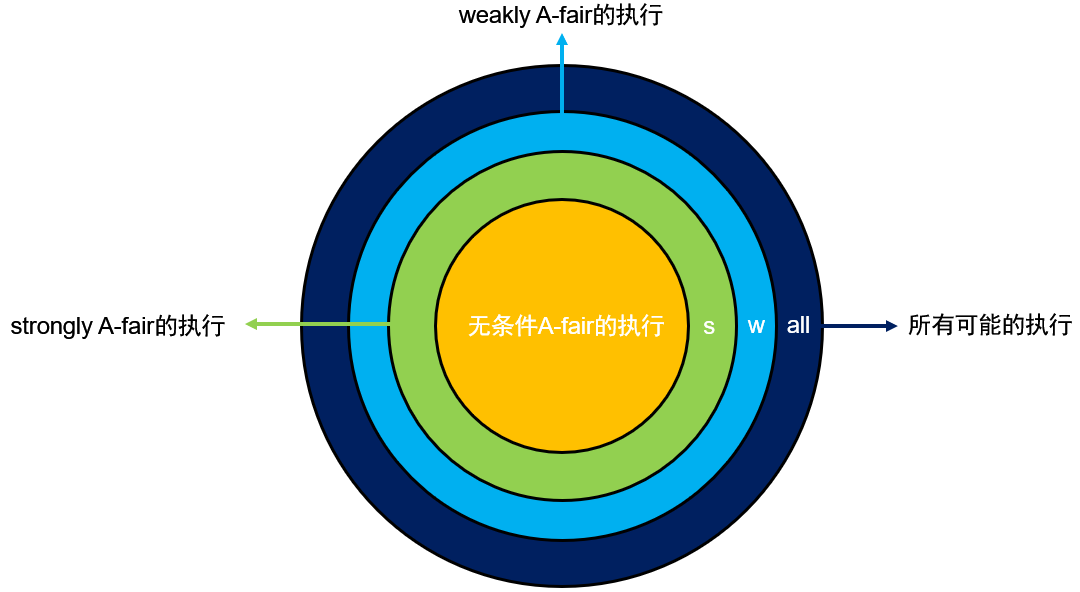
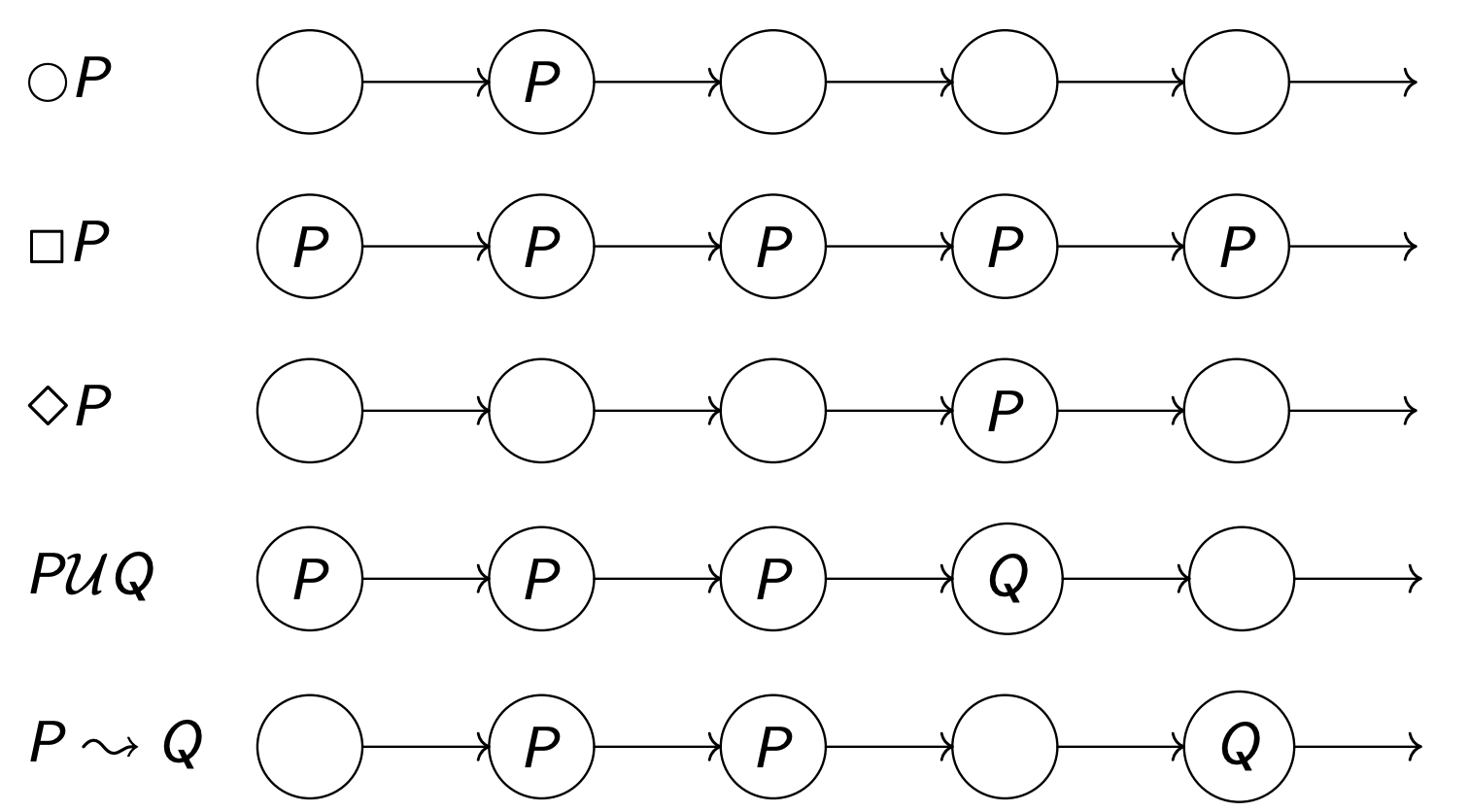
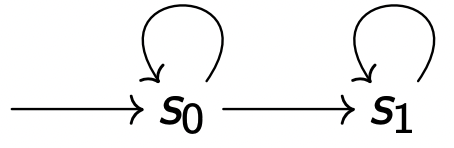
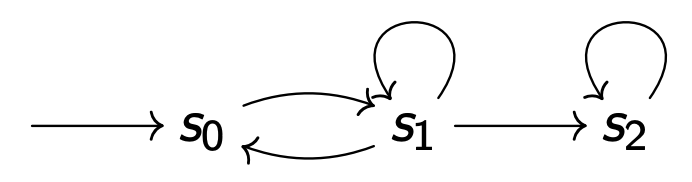
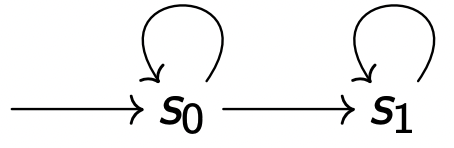 $$
\frac { {s_0}^+ → {s_1}^w \nvDash \Box s_0}{\mathcal{S} \nvDash \Box s_0} \qquad
\frac { {s_0}^w \nvDash \Diamond \neg s_0}{\mathcal{S} \nvDash \Diamond \neg s_0}
$$
$$
\frac { {s_0}^+ → {s_1}^w \nvDash \Box s_0}{\mathcal{S} \nvDash \Box s_0} \qquad
\frac { {s_0}^w \nvDash \Diamond \neg s_0}{\mathcal{S} \nvDash \Diamond \neg s_0}
$$