本文章是根据法国国立高等电力技术、电子学、计算机、水力学与电信学校 (E.N.S.E.E.I.H.T.) 第七学期课程*“Graph Theory”* 总结而来的课程笔记。碍于本人学识有限,部分叙述难免存在纰漏,请读者注意甄别。
一个有限图 G = ( V , E ) G = (V,E) G = ( V , E ) 非空 (non vide) 有限 (fini) 顶点集 (sommets / vertex) V V V
V = { v 0 , v 1 , . . . , v n − 1 } V = \{ v_0, v_1,...,v_{n-1}\}
V = { v 0 , v 1 , . . . , v n − 1 }
和有限边集 (Arête / Edge) E E E
E = { e 0 , e 1 , . . . , e n − 1 } E = \{ e_0, e_1,...,e_{n-1}\}
E = { e 0 , e 1 , . . . , e n − 1 }
其中,每个边 由一对顶点 { v i , v j } \{ v_i, v_j\} { v i , v j } 顶点数 又被称为图的阶数 (ordre)。
相关概念:
如果 n = n b ( V ) n = nb(V) n = n b ( V ) G = ( V , E ) G = (V,E) G = ( V , E ) n 阶 图 n阶图 n 阶 图
如果 e = { v i , v j } e = \{v_i, v_j\} e = { v i , v j } e e e v i v_i v i v j v_j v j 相关 (incidente) ;
如果 e = { v i , v j } e = \{v_i,v_j\} e = { v i , v j } v i v_i v i v j v_j v j 邻接的 (adjacents) ;
两条边 是相邻 的当且仅当它们有一个共同的顶点 ;
e = { v i , v i } e = \{v_i, v_i\} e = { v i , v i } 环 (boucle) ;两个节点之间可能有多条边的图称为多重图 (multigraphe) 。
一个图是简单的 (simple) ,当且仅当
没有环 (boucle) ,
两个顶点之间最多有一条边 (无重边);
一个顶点在图中的度 (degree ) δ ( v i ) δ(v_i) δ ( v i ) v i v_i v i 连接的边的数目 ;
如果每个顶点彼此相邻,即每两个顶点间都有边相连,则称该图是**完全(complet)**图;
Q1 : n阶简单完全图的边数是多少?
# E ( n 阶 简 单 完 全 图 ) = n ( n − 1 ) 2 \# E(n阶简单完全图) = \tfrac{n(n-1)}{2}
# E ( n 阶 简 单 完 全 图 ) = 2 n ( n − 1 )
无向图中,所有顶点度数之和 ∑ d e g ( v ) = 2 ∣ E ∣ ∑deg(v)=2|E| ∑ d e g ( v ) = 2 ∣ E ∣ 奇数度的顶点数必是偶数 。
思考:一种“从无到有”的推广假设
连接两个偶度顶点,这个时候奇度顶点的数量增加2;
连接两个奇度顶点,这个时候奇度顶点的数量减少2;
连接一个奇度顶点和一个偶度顶点,奇度顶点的数量不变。
**k k k k k k
如果一个图 G = ( V , E ) G = (V,E) G = ( V , E ) G G G 有向的(orienté) 。
相关概念:
在一个有向弧 e = ( i , j ) e =(i,j) e = ( i , j ) i i i e e e j j j e e e
对于顶点v v v 出度 δ + ( v ) δ^+(v) δ + ( v ) v v v
入度 δ − ( v ) δ^−(v) δ − ( v ) v v v 总度数 δ ( v ) = δ + ( v ) + δ − ( v ) δ(v) = δ^+(v) + δ^−(v) δ ( v ) = δ + ( v ) + δ − ( v ) ∑ v ∈ V δ ( v ) = 2 × n b ( E ) ∑_{v \in V} δ(v) = 2 \times nb(E) ∑ v ∈ V δ ( v ) = 2 × n b ( E )
由图 G = ( V , E ) G = (V,E) G = ( V , E ) V V V V ′ ⊂ V V ' ⊂ V V ′ ⊂ V G ′ = ( V ′ , E ′ ) G' = (V' , E' ) G ′ = ( V ′ , E ′ ) G G G E ′ E' E ′ E E E V ′ V' V ′
G = ( V , E ) ⟶ V ′ ⊂ V G ′ = ( V ′ , E ′ ) G=(V,E) \quad \stackrel{V'⊂V} \longrightarrow \quad G'=(V',E')
G = ( V , E ) ⟶ V ′ ⊂ V G ′ = ( V ′ , E ′ )
子图:点和边都能在原图中找到
母图:原图
真子图:不等于母图的子图
生成子图:包含所有顶点的子图
基础简单图:从一个图中去掉所有重边及环后所得的剩余图称为基础简单图
点导出子图:顶点是原图顶点的子集且加入两端都在子集中的边构成的图
边导出子图:由原图边集的子集及其所有端点构成的图
I F ( 子 图 i s 完 全 图 ) T H E N ( 完 全 子 图 ) IF(子图 \; is\; 完全图)\quad THEN(完全子图)
I F ( 子 图 i s 完 全 图 ) T H E N ( 完 全 子 图 )
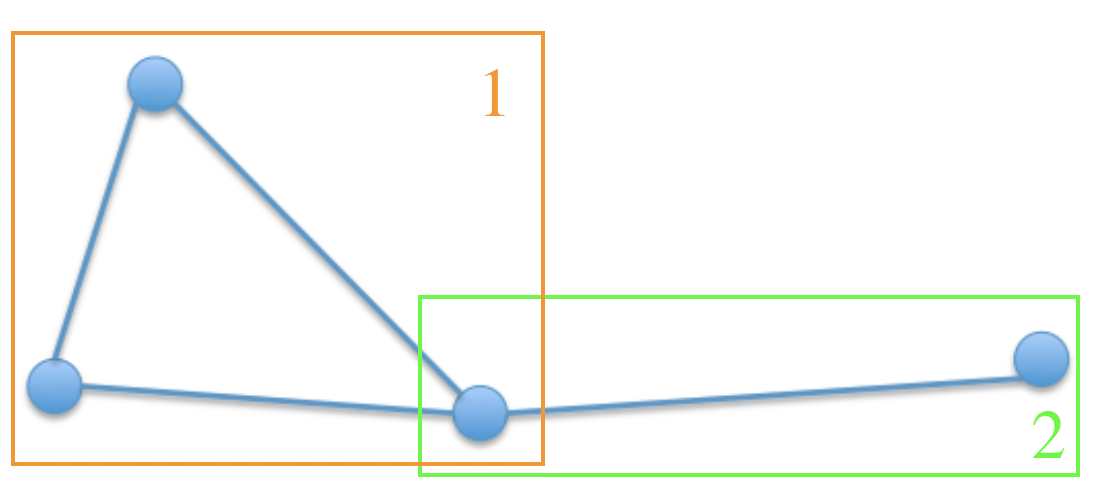
G G G G G G G ′ G' G ′ G G G G ′ G' G ′ G G G
由上图所示,1 和 2 就是原图的两个团。其中 1 是最大团。
G G G G G G
由 E ′ ⊂ E E' ⊂ E E ′ ⊂ E G = ( V , E ) G = (V,E) G = ( V , E ) G ′ = ( V , E ′ ) G'= (V,E') G ′ = ( V , E ′ )
G = ( V , E ) ⟶ E ′ ⊂ E G ′ = ( V , E ′ ) G=(V,E) \quad \stackrel{E'⊂E} \longrightarrow \quad G'=(V,E')
G = ( V , E ) ⟶ E ′ ⊂ E G ′ = ( V , E ′ )
设任意图 G = ( V , E ) G=(V,E) G = ( V , E ) V = v 1 , v 2 , . . . , v n V=v_1,v_2,...,v_n V = v 1 , v 2 , . . . , v n E = e 1 , e 2 , . . . , e ε E=e_1,e_2,...,e_ε E = e 1 , e 2 , . . . , e ε m i j m_{ij} m i j v i v_i v i e j e_j e j 0 , 1 , 2 , … 0,1,2,… 0 , 1 , 2 , … M ( G ) = ( m i j ) n × ε \mathcal{M}(G)=(m_{ij})_{n×ε} M ( G ) = ( m i j ) n × ε 关联矩阵
类似地,有向图 D D D M ( D ) = ( m i j ) n × ε \mathcal{M}(D)=(m_{ij})_{n×ε} M ( D ) = ( m i j ) n × ε m i × j m_{i×j} m i × j
m i j = { 1 v i 是 有 向 边 a j 的 始 点 − 1 v i 是 有 向 边 a j 的 终 点 0 v i 是 有 向 边 a j 的 不 关 联 点 m_{ij}=\begin{cases}
1 \qquad v_i是有向边a_j的始点\\
-1 \qquad v_i是有向边a_j的终点\\
0 \qquad v_i是有向边a_j的不关联点
\end{cases}
m i j = ⎩ ⎪ ⎨ ⎪ ⎧ 1 v i 是 有 向 边 a j 的 始 点 − 1 v i 是 有 向 边 a j 的 终 点 0 v i 是 有 向 边 a j 的 不 关 联 点
设无向图 G = ( V , E ) G=(V,E) G = ( V , E ) V = v 1 , v 2 , . . . , v n V=v_1,v_2,...,v_n V = v 1 , v 2 , . . . , v n E = e 1 , e 2 , . . . , e ε E=e_1,e_2,...,e_ε E = e 1 , e 2 , . . . , e ε a i j a_{ij} a i j v i v_i v i v j v_j v j 0 , 1 , 2 , … 0,1,2,… 0 , 1 , 2 , … A = A ( G ) = ( a i j ) n × n A=A(G)=(a_{ij})_{n×n} A = A ( G ) = ( a i j ) n × n G G G
若干性质:
A ( G ) \mathcal{A}(G) A ( G ) 若 G G G A ( G ) \mathcal{A}(G) A ( G ) i i i v i v_i v i
两图 G G G H H H 同构 的充要条件是存在置换矩阵 P \mathcal{P} P A ( G ) = P T A ( H ) P \mathcal{A}(G) = \mathcal{P}^T\mathcal{A}(H) \mathcal{P} A ( G ) = P T A ( H ) P
类似地,有向图 D D D = A ( D ) ( a i j ) n × n =\mathcal{A}(D)(a_{ij})_{n×n} = A ( D ) ( a i j ) n × n a i j a_{ij} a i j v i v_i v i v j v_j v j 有向边的条数 ,其中 v i v_i v i v j v_j v j D D D
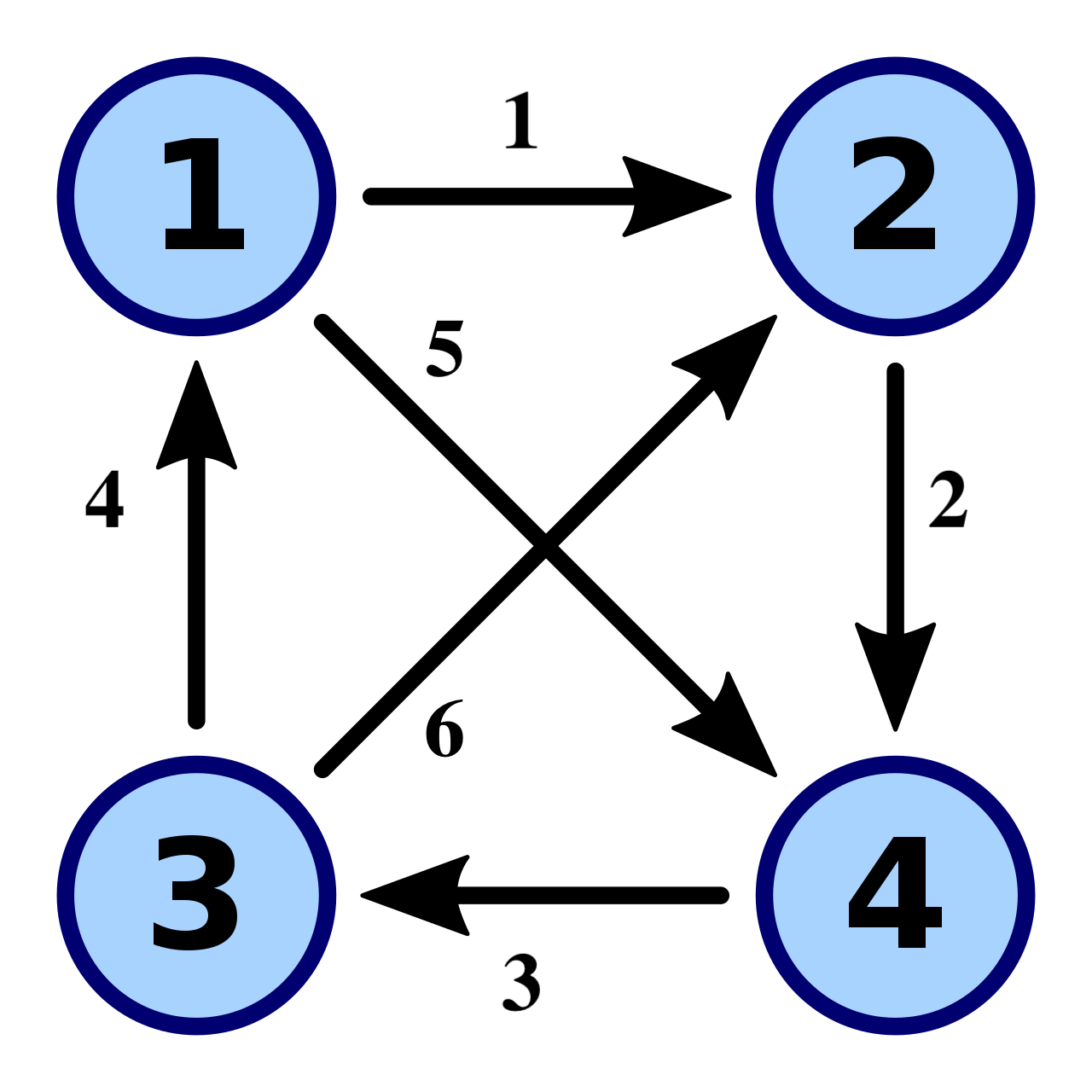
示例,求图中有向图的邻接矩阵和关联矩阵(图中边上的数字为边的编号 ,而非权重):
邻接矩阵为:
[ 0 1 0 1 0 0 0 1 1 1 0 0 0 0 1 0 ] \begin{bmatrix}
0 & 1 & 0 & 1\\
0 & 0 & 0 & 1\\
1 & 1 & 0 & 0\\
0 & 0 & 1 & 0
\end{bmatrix}
⎣ ⎢ ⎢ ⎡ 0 0 1 0 1 0 1 0 0 0 0 1 1 1 0 0 ⎦ ⎥ ⎥ ⎤
关联矩阵为:
[ 1 0 0 − 1 1 0 − 1 1 0 0 0 − 1 0 0 − 1 1 0 1 0 − 1 1 0 − 1 0 ] \begin{bmatrix}
1 & 0 & 0 & -1 & 1 & 0\\
-1 & 1 & 0 & 0 & 0 & -1\\
0 & 0 & -1 & 1 & 0 & 1\\
0 & -1 & 1 & 0 & -1 & 0
\end{bmatrix}
⎣ ⎢ ⎢ ⎡ 1 − 1 0 0 0 1 0 − 1 0 0 − 1 1 − 1 0 1 0 1 0 0 − 1 0 − 1 1 0 ⎦ ⎥ ⎥ ⎤
如果每条弧与正 的实际权重 (poids) 相关联,则对图进行加权。
长度为 q ∈ N q ∈ N q ∈ N ( e 1 , . . . , e q ) (e_1, ..., e_q) ( e 1 , . . . , e q ) q q q 连续相邻边的序列 。 因此存在一个顶点序列 ( v 1 , . . . , v q + 1 ) (v_1,...,v_{q+1}) ( v 1 , . . . , v q + 1 ) v i v_i v i e i − 1 e_{i-1} e i − 1 e i e_i e i
相关概念:
该链被称为连接 顶点 v 1 v_1 v 1 v q + 1 v_{q+1} v q + 1
简单链 (simple) :在边的序列中各边互不相同
基本链 (élémentaire) :在顶点的序列中各顶点互不相同
基本简单链可以称其为 路 (chemin):序列中的边 和顶点 都不相同
如果 v 1 = v q + 1 v_1 = v_{q+1} v 1 = v q + 1
q q q
环是一个**闭合 (fermée)**的单链;
两个顶点间的距离 (Distance) 是两个顶点间最短链的长度 ;
图的直径 (Diamètre) 是图的两个顶点之间的最大距离 。 如果有未连接的顶点,则为 + ∞ +∞ + ∞
无环图 G G G 最多 有 n − 1 n-1 n − 1
proof:
# E 一 般 无 环 图 ≤ # E 无 环 连 通 图 = n − 1 \# E_{一般无环图} \le \# E_{无环连通图} = n-1
# E 一 般 无 环 图 ≤ # E 无 环 连 通 图 = n − 1
如果遍历的顶点除了第一个和最后一个之外是互不相同的,则环是基本的 (élémentaire) 。
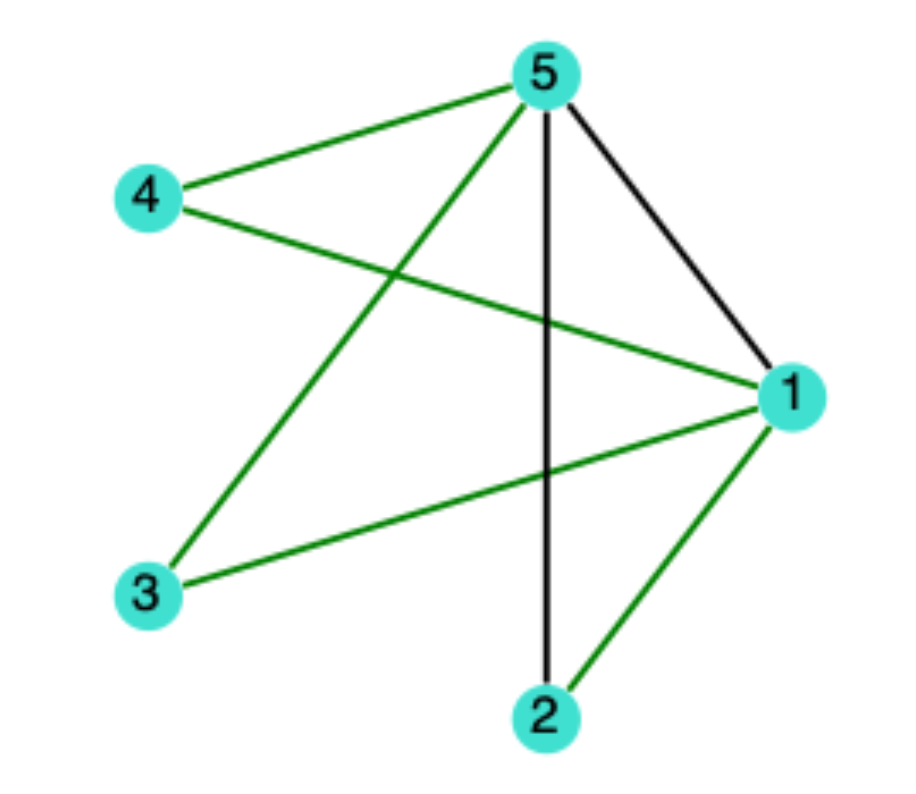
例1:在下图的无向图中,
链 ( 1 , 2 , 5 , 1 , 3 , 5 , 1 ) (1,2,5,1,3,5,1) ( 1 , 2 , 5 , 1 , 3 , 5 , 1 ) 非基本 (non-élémentaire) 闭合 (fermée) 链
链 ( 1 , 2 , 5 , 1 , 3 , ) (1,2,5,1,3,) ( 1 , 2 , 5 , 1 , 3 , ) 非基本 (non-élémentaire) 非闭合 (non-fermée) 链
基本环(基本闭合链):( 1 , 2 , 5 , 1 ) (1,2,5,1) ( 1 , 2 , 5 , 1 )
非基本环(非基本闭合链):( 1 , 2 , 5 , 1 , 3 , 5 , 4 , 1 ) (1,2,5,1,3,5,4,1) ( 1 , 2 , 5 , 1 , 3 , 5 , 4 , 1 )
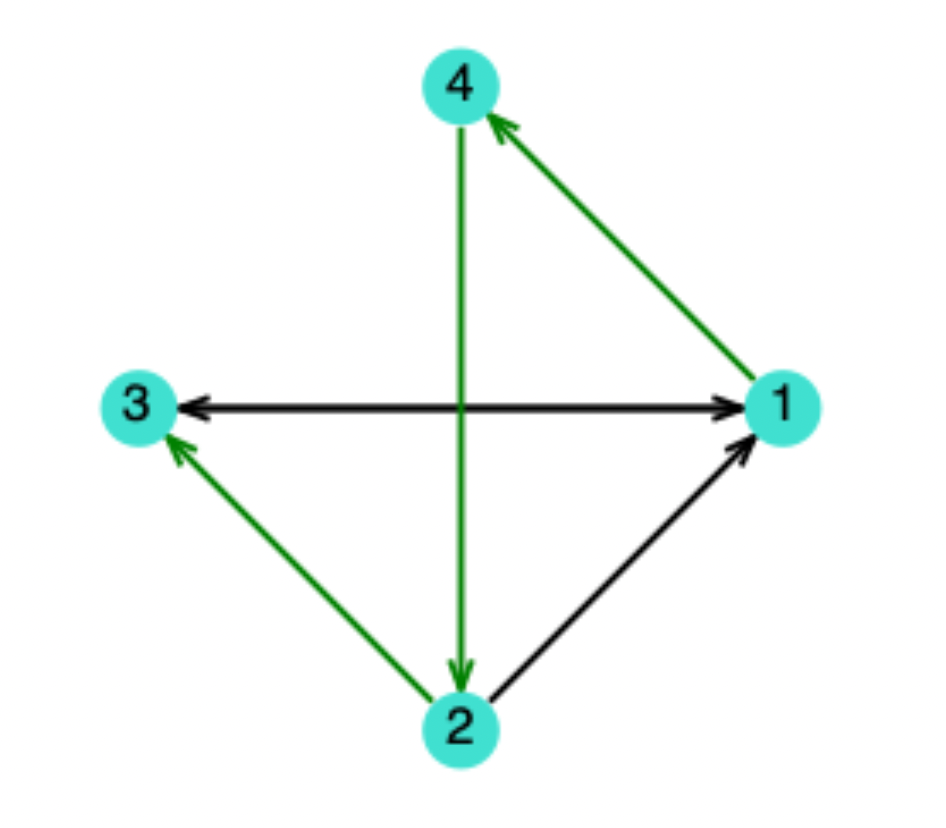
例2 :在下图的有向图中,
基本路径 (chemin: non-fermée) :( 1 , 4 , 2 , 3 ) (1,4,2,3) ( 1 , 4 , 2 , 3 ) 非基本路径:( 1 , 3 , 1 , 4 ) (1,3,1,4) ( 1 , 3 , 1 , 4 )
基本环 (circuit) :( 1 , 4 , 2 , 3 , 1 ) (1,4,2,3,1) ( 1 , 4 , 2 , 3 , 1 )
非基本环 (circuit) :( 1 , 3 , 1 , 4 , 2 , 1 ) (1,3,1,4,2,1) ( 1 , 3 , 1 , 4 , 2 , 1 )
【定义】设连通图 G = ( V , E ) G=(V,E) G = ( V , E ) v i ∈ V v_i \in V v i ∈ V G − v i G - v_i G − v i G G G G G G v i v_i v i G G G v i v_i v i G G G
每个非平凡图至少有两个顶点不是割点
证明:
由于 G G G G G G
注:非平凡树一定有割边,不一定有割点 (K 2 K_2 K 2
有割点的图不是哈密顿图
【性质】设连通图 G = ( V , E ) G=(V,E) G = ( V , E ) v i ∈ V v_i \in V v i ∈ V
v i v_i v i G G G ∃ v x , v y ∈ V , v x ≠ v y , v x 与 v y 间 所 有 的 路 均 通 过 v i ∃ v_x,v_y \in V, v_x \ne v_y, v_x 与 v_y 间所有的路均通过 v_i ∃ v x , v y ∈ V , v x = v y , v x 与 v y 间 所 有 的 路 均 通 过 v i (上一条的普遍推广)∃ V ∖ { v i } 的 划 分 { U , W } ( U ∩ W = ∅ ) , 使 得 ∀ u ∈ U , ∀ w ∈ W : u , w 间 的 路 均 通 过 v i ∃ \; V \setminus \{v_i\} 的划分\{U,W\}(U \cap W = \emptyset),使得\forall u \in U, \forall w \in W: u,w间的路均通过v_i ∃ V ∖ { v i } 的 划 分 { U , W } ( U ∩ W = ∅ ) , 使 得 ∀ u ∈ U , ∀ w ∈ W : u , w 间 的 路 均 通 过 v i
设图 G = ( V , E ) G=(V,E) G = ( V , E ) e i ∈ E e_i \in E e i ∈ E G − e i G - e_i G − e i G G G G G G e i e_i e i G G G e i e_i e i G G G
【性质】设连通图 G = ( V , E ) G=(V,E) G = ( V , E ) e i ∈ E e_i \in E e i ∈ E
e i e_i e i G G G ∃ e x , e y ∈ E , e x ≠ e y , e x 与 e y 间 所 有 的 路 均 " 通 过 " e i ∃ e_x,e_y \in E, e_x \ne e_y, e_x 与 e_y 间所有的路均"通过" e_i ∃ e x , e y ∈ E , e x = e y , e x 与 e y 间 所 有 的 路 均 " 通 过 " e i (上一条的普遍推广)∃ E ∖ { e i } 的 划 分 { U E , W E } ( U E ∩ W E = ∅ ) , 使 得 ∀ u e ∈ U , ∀ w e ∈ W : u e , w e 间 的 路 均 " 通 过 " e i ∃ \; E \setminus \{e_i\} 的划分\{U_E,W_E\}(U_E \cap W_E = \emptyset),使得\forall u_e \in U, \forall w_e \in W: u_e,w_e间的路均"通过"e_i ∃ E ∖ { e i } 的 划 分 { U E , W E } ( U E ∩ W E = ∅ ) , 使 得 ∀ u e ∈ U , ∀ w e ∈ W : u e , w e 间 的 路 均 " 通 过 " e i
e i e_i e i G G G
【性质】
对于不连通或平凡图 G G G κ ( G ) = λ ( G ) = 0 \kappa (G) = \lambda (G) = 0 κ ( G ) = λ ( G ) = 0
对于树 T T T κ ( G ) = λ ( G ) = 1 \kappa (G) = \lambda (G) = 1 κ ( G ) = λ ( G ) = 1
对于有割点的图 G G G κ ( G ) = 1 \kappa (G) = 1 κ ( G ) = 1
对于有割边(桥)的图 G G G λ ( G ) = 1 \lambda (G) = 1 λ ( G ) = 1
对于完全图 K p K_p K p κ ( G ) = λ ( G ) = p − 1 \kappa (G) = \lambda (G) = p-1 κ ( G ) = λ ( G ) = p − 1
图 G 连 通 ⇔ κ ( G ) ≥ 1 图G连通 \Leftrightarrow \kappa (G) \ge 1 图 G 连 通 ⇔ κ ( G ) ≥ 1 对于一个环(圈)C n , n ≥ 3 C_n, n ≥ 3 C n , n ≥ 3 κ ( C n ) = 2 κ(C_n) = 2 κ ( C n ) = 2
除了 κ ( G ) \kappa (G) κ ( G ) λ ( G ) \lambda (G) λ ( G ) δ ( G ) \delta (G) δ ( G ) G G G
设 G 是 n 阶 简 单 图 , 若 δ ( G ) ≥ ⌊ n 2 ⌋ , 则 G 必 连 通 , 且 λ ( G ) = δ ( G ) . 设 G 是 n 阶简单图,若 δ(G) ≥ ⌊\frac{n}{2}⌋,则 G 必连通,且 λ(G) = δ(G).
设 G 是 n 阶 简 单 图 , 若 δ ( G ) ≥ ⌊ 2 n ⌋ , 则 G 必 连 通 , 且 λ ( G ) = δ ( G ) .
证明:
若 G G G G G G
∣ V ( H ) ∣ ≤ ⌊ n 2 ⌋ |V(H)| ≤ ⌊\frac{n}{2}⌋
∣ V ( H ) ∣ ≤ ⌊ 2 n ⌋
因 G G G
∆ ( H ) ≤ ⌊ n 2 ⌋ − 1 < ⌊ n 2 ⌋ ∆(H) ≤ ⌊\frac{n}{2}⌋ − 1 < ⌊\frac{n}{2}⌋
∆ ( H ) ≤ ⌊ 2 n ⌋ − 1 < ⌊ 2 n ⌋
于是
δ ( G ) ≤ δ ( H ) ≤ ∆ ( H ) < ⌊ n 2 ⌋ δ(G) ≤ δ(H) ≤ ∆(H) < ⌊\frac{n}{2}⌋
δ ( G ) ≤ δ ( H ) ≤ ∆ ( H ) < ⌊ 2 n ⌋
这与已知矛盾,所以 G G G
【定理】对任意的图 G = ( V , E ) G=(V,E) G = ( V , E )
κ ( G ) ≤ λ ( G ) ≤ δ ( G ) κ(G) ≤ λ(G) ≤ δ(G)
κ ( G ) ≤ λ ( G ) ≤ δ ( G )
在一个无向图 G G G v i { v_{i}} v i v j v_{j} v j 相连 (当然从 v j v_{j} v j 也 一 定 有 路 径 ) , 则 称 也一定有路径),则称 也 一 定 有 路 径 ) , 则 称 v j v_{j} v j
如果 G G G 有向图 ,那么连接 v i v_{i} v i v j v_{j} v j 同向 。
如果图中任意两点都是连通的 ,那么图被称作连通图 。图的连通性是图的基本性质。连通度 是指为了让图分解成孤立的子图所要删除的顶点数的最小值。
设连通图 G G G n n n G G G 至少 有 n − 1 n-1 n − 1
Proof:
A graph with n n n n n n at most one. So beginning with a graph with no edge, adding one edge at a time till the graph has k k k at most k k k n n n k k k at least n − k n−k n − k n n n n − 1 n-1 n − 1 at least two components, and is disconnected. Therefore every connected graph with n n n at least n − 1 n-1 n − 1 P n P_n P n
一个有向图被称作弱连通 (weakly connected )的,如果将所有有向边替换为无向边之后的无向图是连通的,如果对于任意一对顶点 u u u v v v u u u v v v u u u v v v 单连通 (unilaterally conncected )的。
对 于 任 意 一 对 顶 点 ( u , v ) , 存 在 路 径 u → v , 不 存 在 路 径 v → u 对于任意一对顶点(u,v),\; 存在路径u \to v,\; 不存在路径v\to u
对 于 任 意 一 对 顶 点 ( u , v ) , 存 在 路 径 u → v , 不 存 在 路 径 v → u
如果对于如果对于任意一对顶点 u u u v v v u u u v v v v v v u u u 强连通 (strongly connected )的
对 于 任 意 一 对 顶 点 ( u , v ) , 存 在 路 径 u → v , 且 存 在 路 径 v → u 对于任意一对顶点(u,v),\; 存在路径u \to v,\; 且存在路径v\to u
对 于 任 意 一 对 顶 点 ( u , v ) , 存 在 路 径 u → v , 且 存 在 路 径 v → u
集合 X X X Y Y Y R = ( X , Y , G ( R ) ) \mathcal{R}=(X,Y,G(\mathcal{R})) R = ( X , Y , G ( R ) ) G ( R ) G(\mathcal{R}) G ( R ) R \mathcal{R} R 图 ,是笛卡儿积 X × Y X\times Y X × Y ( x , y ) ∈ G ( R ) (x,y) ∈ G(\mathcal{R}) ( x , y ) ∈ G ( R ) x 与 y 有 关 系 于 R x\;与\;y\;有关系于 \mathcal{R} x 与 y 有 关 系 于 R x R y x\mathcal{R}y x R y R ( x , y ) \mathcal{R}(x,y) R ( x , y )
否则称 x 与 y 无 关 系 R x \; 与 \; y \; 无关系\mathcal{R} x 与 y 无 关 系 R R ⊆ X × Y \mathcal{R}⊆X×Y R ⊆ X × Y R \mathcal{R} R
关系的性质主要有以下五种:自反性,反自反性,对称性,反对称性和传递性。
自反性 (réfexivité) :在集合 X X X R \mathcal{R} R x ∈ E x \in E x ∈ E ( x , x ) ∈ R (x,x) \in \mathcal{R} ( x , x ) ∈ R R 是自反的。
∀ x ∈ E , x R x \forall x \in E,\quad x \mathcal{R} x
∀ x ∈ E , x R x
非自反性(自反性的否定的强型式):在集合 X X X R \mathcal{R} R x ∈ X x\in X x ∈ X ( x , x ) ∉ R (x,x)\notin R ( x , x ) ∈ / R
∀ x ∈ A , ( x , x ) ∉ R \forall x\in A, (x,x)\notin \mathcal{R}
∀ x ∈ A , ( x , x ) ∈ / R
对称性 (symétrie) :在集合 X X X R \mathcal{R} R ( x , y ) ∈ R (x,y) \in \mathcal{R} ( x , y ) ∈ R ( y , x ) ∈ R (y,x) \in \mathcal{R} ( y , x ) ∈ R
∀ ( x , y ) ∈ E 2 , x R y ⇒ y R x \forall (x,y) \in E^2,\quad x \mathcal{R} y \Rightarrow y \mathcal{R} x
∀ ( x , y ) ∈ E 2 , x R y ⇒ y R x
∀ ( x , y ) ∈ E 2 , ( x , y ) ∈ R ⇒ ( y , x ) ∉ R \forall (x,y) \in E^2, \quad (x,y) \in \mathcal{R} \Rightarrow (y,x) \notin \mathcal{R}
∀ ( x , y ) ∈ E 2 , ( x , y ) ∈ R ⇒ ( y , x ) ∈ / R
∀ ( x , y ) ∈ E 2 , ( ( x R y ) ∧ ( y R x ) ⇒ x = y ) \forall (x,y) \in E^2, \quad ((x \mathcal{R} y) \land (y \mathcal{R} x) \Rightarrow x=y)
∀ ( x , y ) ∈ E 2 , ( ( x R y ) ∧ ( y R x ) ⇒ x = y )
∀ ( x , y , z ) ∈ E 3 , ( ( x R y ) ∧ ( y R z ) ⇒ x R z \forall (x,y,z) \in E^3, \quad ((x \mathcal{R} y) \land (y \mathcal{R} z) \Rightarrow x \mathcal{R} z
∀ ( x , y , z ) ∈ E 3 , ( ( x R y ) ∧ ( y R z ) ⇒ x R z
设 R \mathcal{R} R E E E R \mathcal{R} R 充要条件 :
R \mathcal{R} R E E E I E ⊆ R I_{E}\subseteq \mathcal{R} I E ⊆ R R \mathcal{R} R E E E R \mathcal{R} R E E E R = R − 1 \mathcal{R} = \mathcal{R} ^{-1} R = R − 1 R \mathcal{R} R E E E R \mathcal{R} R E E E R ∩ R − 1 = ∅ \mathcal{R} \cap \mathcal{R}^{-1}= \emptyset R ∩ R − 1 = ∅ R \mathcal{R} R E E E R ∘ R ⊆ R \mathcal{R} \circ \mathcal{R}\subseteq \mathcal{R} R ∘ R ⊆ R
等价关系 也称为同值关系(英语:Equivalence relation)即设 R \mathcal{R} R E E E R \mathcal{R} R
自反性 (réfexivité):∀ x ∈ E , x R x \forall x \in E, \quad x \mathcal{R} x ∀ x ∈ E , x R x
对称性 (symétrie):∀ ( x , y ) ∈ E 2 , x R y ⇒ y R x \forall (x,y) \in E^2, \quad x \mathcal{R} y \Rightarrow y \mathcal{R}x ∀ ( x , y ) ∈ E 2 , x R y ⇒ y R x
传递性 (transitivité):∀ ( x , y , z ) ∈ E 3 , ( ( x R y ) ∧ ( y R z ) ⇒ x R z \forall (x,y,z) \in E^3, \quad ((x \mathcal{R} y) \land (y \mathcal{R} z) \Rightarrow x \mathcal{R} z ∀ ( x , y , z ) ∈ E 3 , ( ( x R y ) ∧ ( y R z ) ⇒ x R z
例如,设 E = 1 , 2 , . . . , 8 E={1,2,...,8} E = 1 , 2 , . . . , 8 E E E R \mathcal{R} R
x R y ⟺ ∀ ( x , y ) ∈ E , x ≡ y ( m o d 3 ) x \mathcal{R} y \Longleftrightarrow \forall (x,y) \in E, x \equiv y(mod \; 3)
x R y ⟺ ∀ ( x , y ) ∈ E , x ≡ y ( m o d 3 )
其中,x ≡ y ( m o d 3 ) x \equiv y(mod \; 3) x ≡ y ( m o d 3 ) x x x y 模 3 y模3 y 模 3 x x x y y y 1 R 4 1\mathcal{R} 4 1 R 4 2 R 5 2\mathcal{R}5 2 R 5 3 R 6 3\mathcal{R}6 3 R 6 R \mathcal{R} R E E E
并非所有的二元关系都是等价关系。一个简单的反例是比较两个数中哪个较大 :
没有自反性:任何一个数不能比自身为较大 n ≯ n n\ngtr n n ≯ n
没有对称性:如果 m > n m>n m > n n > m n>m n > m
令 R \mathcal{R} R E E E x x x E E E x x x E E E x x x [ x ] [x] [ x ]
[ x ] = y ∈ E , x R y [x] = {y ∈ E,x\mathcal{R}y}
[ x ] = y ∈ E , x R y
设 R \mathcal{R} R E E E
证明:
I F ( v k = { v j } ∪ { v i } ) T H E N ( v i R v k , v j R v k ⇒ v i R v j ⇒ [ v i ] = [ v j ] ) E L S E ( { v j } ∩ { v i } = ∅ ) \begin{aligned} IF (v_k = \{v_j\} \cup \{v_i\}) \quad
& THEN(v_i \mathcal{R} v_k,\;v_j \mathcal{R} v_k \Rightarrow v_i \mathcal{R} v_j \Rightarrow [v_i]=[v_j]) \\
& ELSE(\{v_j\} \cap \{v_i\} = \emptyset)
\end{aligned}
I F ( v k = { v j } ∪ { v i } ) T H E N ( v i R v k , v j R v k ⇒ v i R v j ⇒ [ v i ] = [ v j ] ) E L S E ( { v j } ∩ { v i } = ∅ )
设 R \mathcal{R} R E E E E E E
设 G G G v i v_i v i v j v_j v j v i v_i v i v j v_j v j v j v_j v j v i v_i v i v i R v j v_i \mathcal{R} v_j v i R v j R \mathcal{R} R v i v_i v i
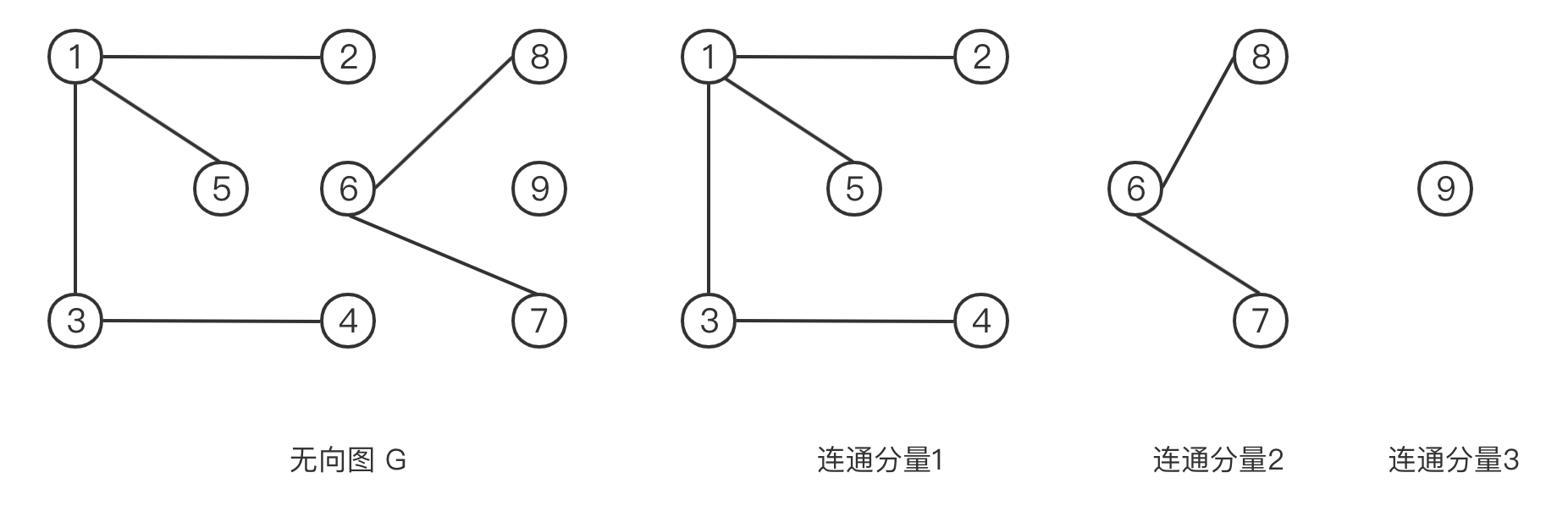
无向图 G G G 极大连通子图 称为 G G G 连通分量 ( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。对于分量中任意两点 u , v u,v u , v u u u v v v v v v u u u
如下图所示,
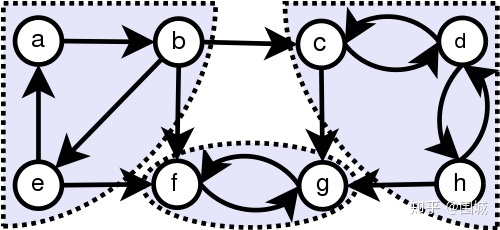
有向图 G = ( V , E ) G= (V,E) G = ( V , E ) 极大强连通子图 称为 G G G 强连通分量 ,强连通图只有一个强连通分量,即是其自身。非强连通的有向图有多个强连通分量。极大连通分量。一个连通分量加上任何一些点都不是连通分量了,该连通分量就是强连通分量。
强连通分量的作用: 将任意有向图通过 缩点(将所有连通分量缩成一个点) 转换成有向无环图( D A G DAG D A G
前驱:P r e d ( S ⊆ V e r t e x ) = { v ′ ∣ v ∈ S , ( v ′ , v ) ∈ E d g e } Pred (S \subseteq V_{ertex}) = \{v' | v \in S, (v',v) \in E_{dge}\} P r e d ( S ⊆ V e r t e x ) = { v ′ ∣ v ∈ S , ( v ′ , v ) ∈ E d g e }
后继:S u c c ( S ⊆ V e r t e x ) = { v ′ ∣ v ∈ S , ( v , v ′ ) ∈ E d g e } Succ (S \subseteq V_{ertex}) = \{v' | v \in S, (v,v') \in E_{dge}\} S u c c ( S ⊆ V e r t e x ) = { v ′ ∣ v ∈ S , ( v , v ′ ) ∈ E d g e }
我们还通过以下方式定义前驱 和后继 的自反和传递闭包:
P r e d ∗ ( S ⊆ V e r t e x ) = S ∪ P r e d ∗ ( P r e d ( S ) ) Pred^* (S \subseteq V_{ertex}) = S \cup Pred^* (Pred(S)) P r e d ∗ ( S ⊆ V e r t e x ) = S ∪ P r e d ∗ ( P r e d ( S ) ) S u c c ∗ ( S ⊆ V e r t e x ) = S ∪ S u c c ∗ ( S u c c ( S ) ) Succ^* (S \subseteq V_{ertex}) = S \cup Succ^* (Succ(S)) S u c c ∗ ( S ⊆ V e r t e x ) = S ∪ S u c c ∗ ( S u c c ( S ) )
1 2 3 4 5 6 7 CFG_G <- ∅空集 WHILE (有一个顶点不在 CFC_G 子集的并集中) DO 选择 v ∈ V 不出现 CFC_G 子集的并集 CFC_v <- SUCC*({v}) ∩交集 Pred*({v}) CFC_G <- CFC_G ∪并集 {CFC_v} END
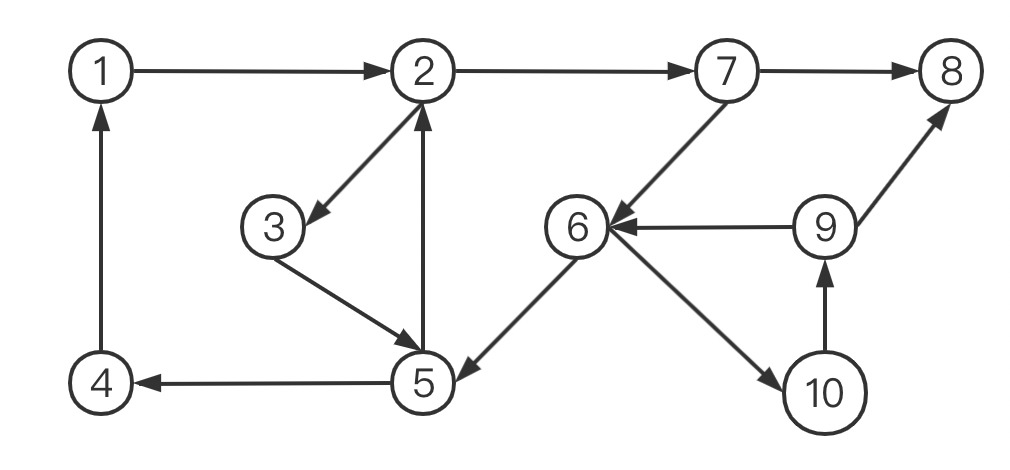
例:应用 Demoucron 算法找出下图中的强连通分量:
C F C G = ∅ CFC_G = \emptyset C F C G = ∅ C F C v 1 = { 1 , 2 , 3 , 7 , 5 , 6 , 8 , 4 , 10 , 9 } ← 顺 箭 头 方 向 S u c c ∩ { 1 , 4 , 5 , 3 , 6 , 2 , 7 , 9 , 10 } ← 逆 箭 头 方 向 P r e d = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 9 , 10 } \begin{aligned} CFC_{v_1} & = \{1,2,3,7,5,6,8,4,10,9\} \quad \leftarrow 顺箭头方向_{Succ} \\ & \quad \cap \; \{ 1,4,5,3,6,2,7,9,10\} \quad \leftarrow 逆箭头方向_{Pred} \\ & = \{ 1,2,3,4,5,6,7,9,10\} \end{aligned} C F C v 1 = { 1 , 2 , 3 , 7 , 5 , 6 , 8 , 4 , 1 0 , 9 } ← 顺 箭 头 方 向 S u c c ∩ { 1 , 4 , 5 , 3 , 6 , 2 , 7 , 9 , 1 0 } ← 逆 箭 头 方 向 P r e d = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 9 , 1 0 } v 8 并 不 在 上 一 轮 的 C F C v 中 v_8 \;并不在上一轮的\;CFC_v 中 v 8 并 不 在 上 一 轮 的 C F C v 中 C F C G = { [ 1 ] , [ 8 ] } → { [ 8 ] } s e u l CFC_G = \{ [1] , [8] \} \rightarrow \{ [8] \}_{seul} C F C G = { [ 1 ] , [ 8 ] } → { [ 8 ] } s e u l
树 是一个无环连通图 。森林 由若干个树连接 得来(无环)。
由 k k k m = n − k m = n − k m = n − k n n n G G G m m m G G G
Theorem:
每 棵 非 平 凡 树 至 少 有 两 片 树 叶 每棵非平凡树至少有两片树叶
每 棵 非 平 凡 树 至 少 有 两 片 树 叶
证明 :
设 d 1 ≤ d 2 ≤ ⋅ ⋅ ⋅ ≤ d n d_1 ≤ d_2 ≤ · · · ≤ dn d 1 ≤ d 2 ≤ ⋅ ⋅ ⋅ ≤ d n T T T T T T T T T δ ( T ) = d 1 ≥ 1 δ(T) = d_1 ≥ 1 δ ( T ) = d 1 ≥ 1 T T T 2 n − 2 = 2 m ( T ) = ∑ i = 1 n d i ≥ 1 + 2 ( n − 1 ) 2n − 2 = 2m(T) = \sum_{i=1}^n d_i ≥ 1 + 2(n − 1) 2 n − 2 = 2 m ( T ) = ∑ i = 1 n d i ≥ 1 + 2 ( n − 1 )
n : = NB of vertex m : = NB of Edge t : = NB of vertex with 1 degre ∵ G is a tree ∴ G is a connected graph ∴ ∑ δ ( v ) = 2 m = 2 ( n − 1 ) according to n=m-1 ∵ ∑ δ ( v ) ≥ 2 δ ( v ) ≥ 2 ( n − t ) + t ∴ 2 ( n − 1 ) ≥ 2 ( n − t ) + t ⇒ t ≥ 2 n := \text{NB of vertex}\\
m := \text{NB of Edge}\\
t := \text{NB of vertex with 1 degre}\\
\because \text{G is a tree}\quad
\therefore \text{G is a connected graph}\\
\therefore \sum \delta(v) = 2m = 2(n-1) \quad \text{according to n=m-1} \\
\because \sum_{\delta(v) \ge 2} \delta(v) \ge 2(n-t)+t \\
\therefore 2(n-1) \ge 2(n-t)+t \quad \Rightarrow \quad t \ge 2
n : = NB of vertex m : = NB of Edge t : = NB of vertex with 1 degre ∵ G is a tree ∴ G is a connected graph ∴ ∑ δ ( v ) = 2 m = 2 ( n − 1 ) according to n=m-1 ∵ δ ( v ) ≥ 2 ∑ δ ( v ) ≥ 2 ( n − t ) + t ∴ 2 ( n − 1 ) ≥ 2 ( n − t ) + t ⇒ t ≥ 2
设 G G G n n n m m m 等价 :
G G G G G G 无环 且任意两个不同点之间存在唯一的路;G G G G G G 连通 ,且 n = m − 1 n = m - 1 n = m − 1 G G G 无圈 ,且 n = m − 1 n = m - 1 n = m − 1 G G G 唯一 的圈。
G G G 生成树 (arbre couvrant)是具有 G G G 全部顶点 ,但边数最少 的连通子图 。
若有图 G = ( V G , E G ) G=(V_G, E_G) G = ( V G , E G ) T = ( V T , E T ) T = (V_T, E_T) T = ( V T , E T ) V T = V G V_T = V_G V T = V G E T ⊂ E G E_T \subset E_G E T ⊂ E G T T T G G G
带权图的生成树中,总权重最小的称为最小生成树 。
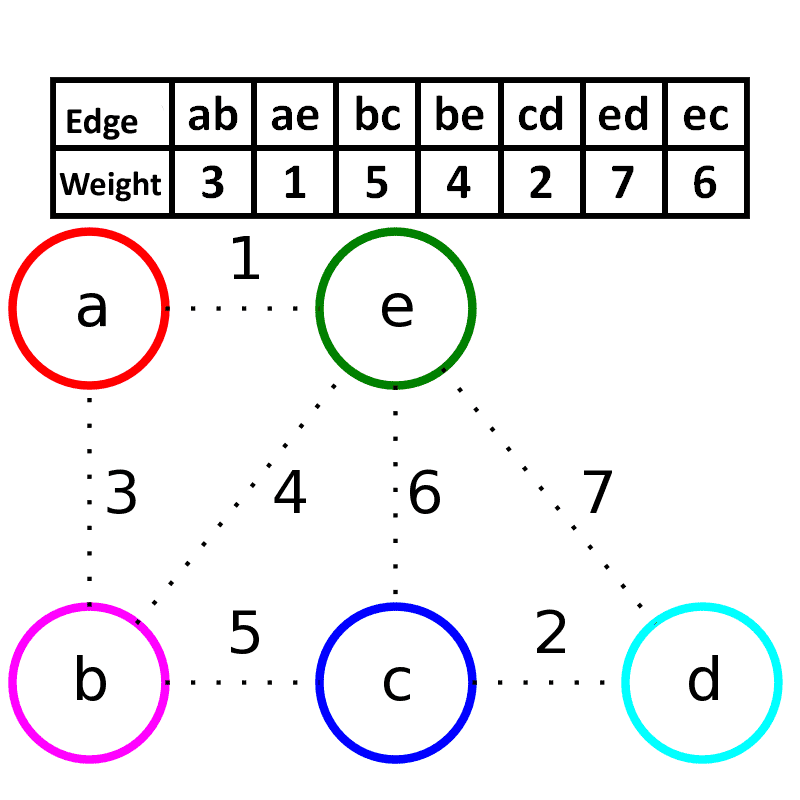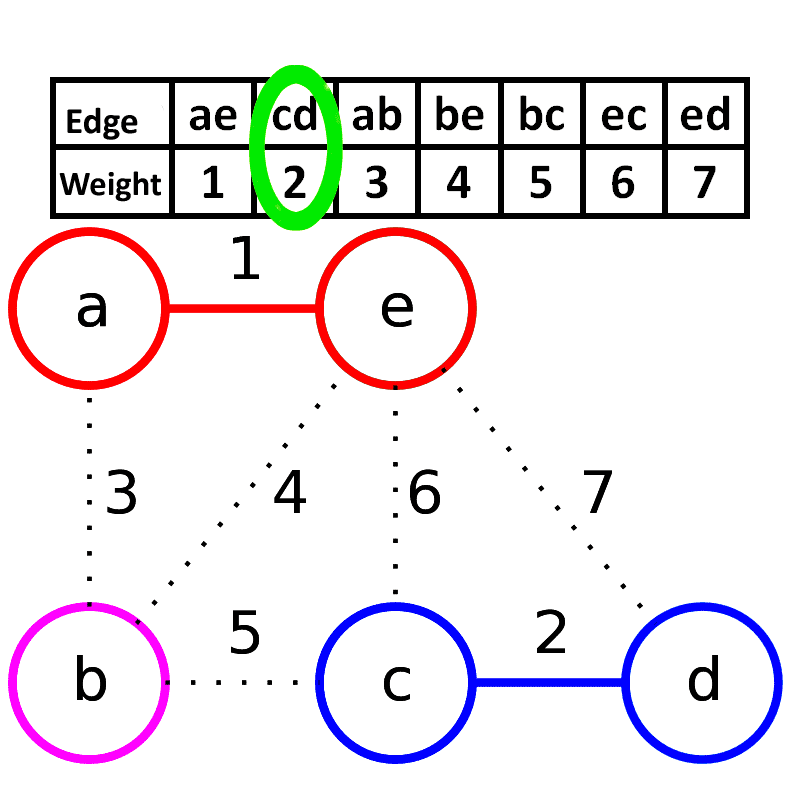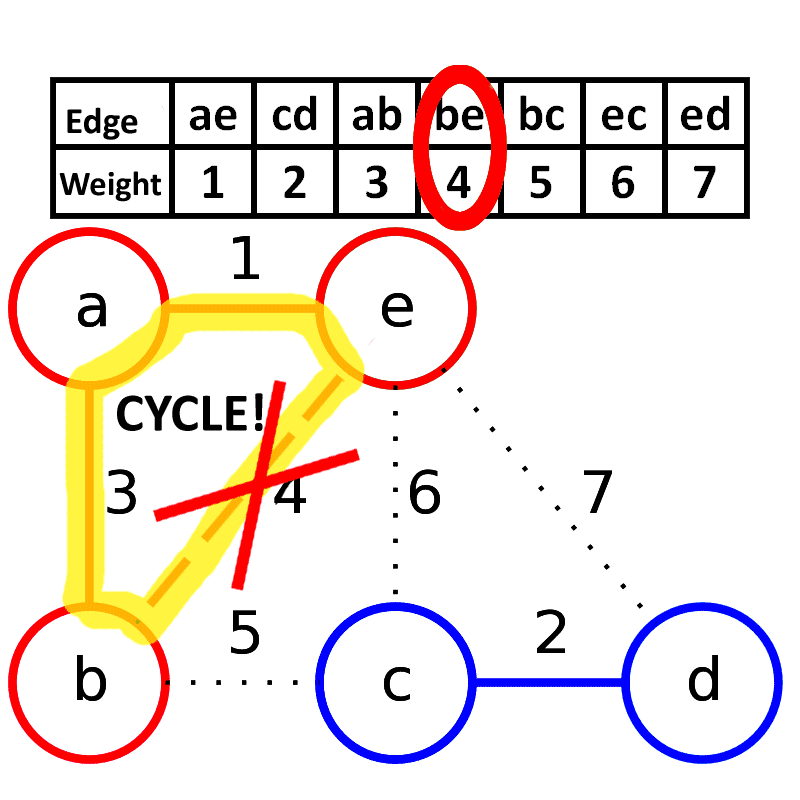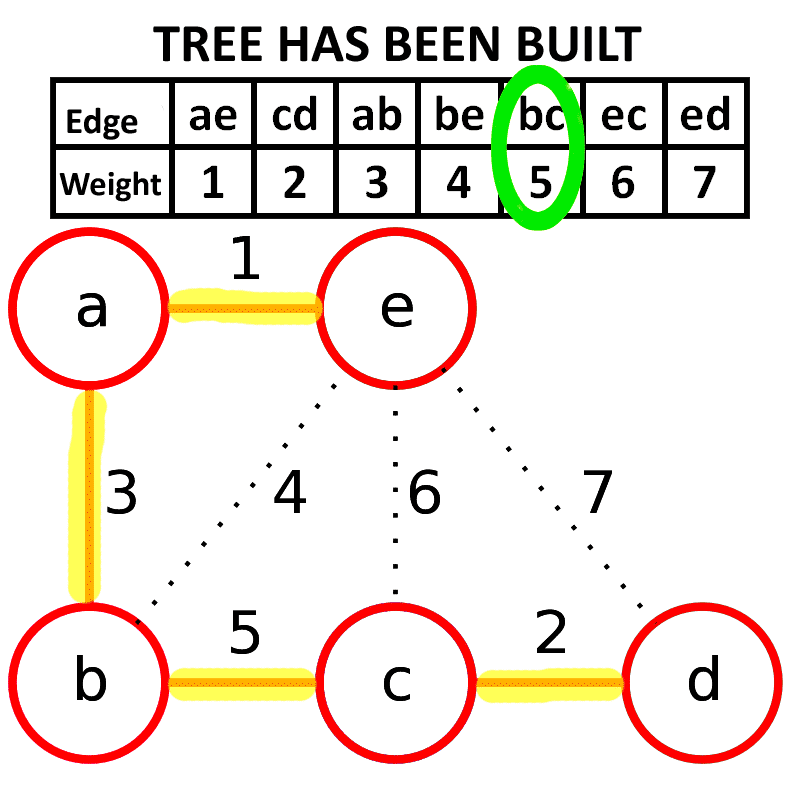
求取最小生成树的算法:一种贪心算法
新建图 G G G G G G
将原图中所有的边按权值从小到大升序 ;
从权值最小的边开始 ,如果这条边连接的两个节点于图 G G G G G G 重复3,直至图 G G G
Theorem
假定 G G G 连通图 ,则下列命题等价:
G G G 欧拉图 ;
G G G 都是偶数 或 只有 2 个顶点是奇数度,其余均为偶数度 ;
连通无向图 G G G G G G
连通无向图 G G G u , v u,v u , v u u u v v v
G G G
无向图
连通无向图 G G G G G G
连通无向图 G G G u , v u,v u , v u u u v v v
有向图
强连通图有向图 D D D 欧拉回路 当且仅当 D D D 每个顶点的出度数和入读数相同 **单向连通有向图 D D D u u u v v v 欧拉通路 当且仅当 u u u 出度数 比入度数大 1v v v 入度数 比出度数 大 1D D D 入度数 和出度数 相同
Hierholzer算法用于在连通图寻找欧拉迹,其流程非常简单。
从一个可能的起点出发,进行深度优先搜索 ,但是每次沿着辅助边从某个顶点移动到另外一个顶点的时候,都需要删除这个辅助边。如果没有可移动的路径,则将所在结点加入到栈中,并返回。
最后得到的栈中保存的就是整个欧拉闭迹中的顶点。
1 2 3 4 5 6 7 dfs(node, trace){ while (!node.adj.isEmpty()){ Node next = node.adj.removeLast(); dfs(next, trace); } trace.addLast(node); }
若存在 v i ∈ V v_i \in V v i ∈ V v i v_i v i δ ( v i ) = 1 \delta(v_i) =1 δ ( v i ) = 1 n > 1 n>1 n > 1
若存在 v i ∈ V v_i ∈ V v i ∈ V v i v_i v i δ ( v ) = 2 δ(v) = 2 δ ( v ) = 2 v i v_i v i
K n K_n K n 有向完全图中必存在哈密顿通路
强连通的有向完全图中必存在哈密顿回路
Theorem (Ore,充分条件)
对于阶 n ≥ 3 n ≥ 3 n ≥ 3 G G G G G G 任意 两个不相邻顶点 u u u v v v
δ ( u ) + δ ( v ) ≥ n , \delta(u) + \delta(v) ≥ n,
δ ( u ) + δ ( v ) ≥ n ,
那么 G G G
证明 :
等效地表明,每个非哈密顿图G都不满足条件。因此,令 G G G n ≥ 3 n≥3 n ≥ 3 G G G H H H
令 u u u v v v H H H ( u , v ) (u, v) ( u , v ) H H H H H H ( u , v ) (u,v) ( u , v ) v 1 , v 2 , . . . v n v_1, v_2, ... v_n v 1 , v 2 , . . . v n u = v 1 u = v_1 u = v 1 v = v n v = v_n v = v n
对于 2 ≤ i ≤ n 2≤i≤n 2 ≤ i ≤ n i i i H H H v 1 v_1 v 1 v i v_i v i v ( i − 1 ) v_(i-1) v ( i − 1 ) v n v_n v n H H H v 1 , v 2 . . . v ( i − 1 ) , v n , v ( n − 1 ) . . . v i v_1,v_2 ... v_(i-1), v_n, v_{(n-1)} ... v_i v 1 , v 2 . . . v ( i − 1 ) , v n , v ( n − 1 ) . . . v i
因此,入射到 v 1 v_1 v 1 v n v_n v n i i i n − 1 n-1 n − 1 H H H δ ( v 1 ) + δ ( v n ) δ(v_1) + δ(v_n) δ ( v 1 ) + δ ( v n ) n n n G G G H H H G G G
Theorem (Dirac,充分条件)
对于 n ≥ 3 n ≥ 3 n ≥ 3 G G G G G G
δ ( G ) ≥ n 2 \delta(G) ≥ \frac{n}{2}
δ ( G ) ≥ 2 n
那么 G G G
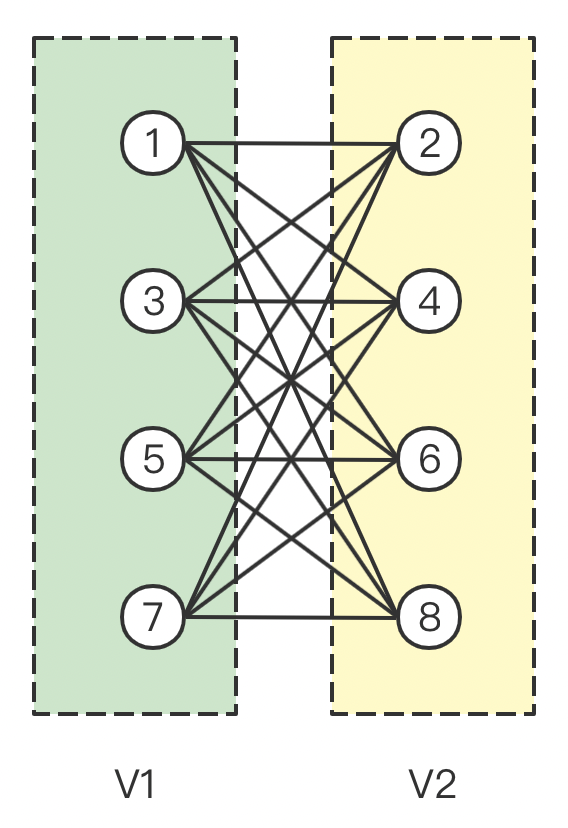
二分图又称作二部图,是图论中的一种特殊模型。 设 G = ( V , E ) G=(V,E) G = ( V , E ) V V V 互不相交的子集 A A A B B B ( v i , v j ) (v_i, v_j) ( v i , v j ) v i v_i v i v i ∈ A v_i \in A v i ∈ A v j ∈ B v_j \in B v j ∈ B G G G 二分图 。
简而言之,就是顶点集 V V V 两个互不相交的子集 ,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻 。
如下图,
完全二分图:V 1 V_1 V 1 V 2 V_2 V 2 p p p q q q 𝐾 𝑝 , 𝑞 𝐾_{𝑝,𝑞} K p , q
性质
如果一个图 G = ( V , E ) G=(V,E) G = ( V , E ) ∣ n b ( V 1 ) − n b ( V 2 ) ∣ > 1 | nb(V_1) - nb(V_2)| > 1 ∣ n b ( V 1 ) − n b ( V 2 ) ∣ > 1 G G G
若无向图 G G G G G G
非平凡无向图 G G G G G G
Dijkstra算法是一种经典的基于贪心 的单源最短路算法,其要求图中的边全部非负。
设 G = ( V , E ) G=(V,E) G = ( V , E ) V V V
第一组为已求出最短路径的顶点集合 (用 S S S S S S 源点 ,以后每求得一条最短路径 , 就将加入到集合 S S S S S S
第二组为其余未确定最短路径的顶点集合 (用 U U U S S S v 0 v_0 v 0 S S S v 0 v_0 v 0 U U U
此外,每个顶点对应一个距离,S S S v 0 v_0 v 0 U U U v 0 v_0 v 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 DIJKSTRA(G, w, s) // s的当前最短路长度是0,其他节点的当前最短路长度是+∞。 INITIALIZE-SINGLE-SOURCE(G, s) // S是节点集合(V的子集),其中每个节点u都已经求得了全图最短路。 // 初期所有节点都没求得全图最短路。 S ← ∅ // Q是一个节点的优先队列,包含所有尚未求得全图最短路的节点。Q中的节点按照当前最短路的长度从小到大排序。 // 初期所有节点都没求得全图最短路,所以都在Q中。 Q ← V[G] // 循环直到Q中所有节点都清空(都移动到S),即所有节点都已经求出全图最短路。 while Q ≠ ∅ // 从Q中取出当前最短路长度最小的节点u // 并认为u的当前最短路就是全图最短路。(这个不是那么显然,后续有说明) do u ← EXTRACT-MIN(Q) // 将u放进集合S中,即标注为“已求得u的全图最短路”。 S ← S∪{u} // 对于u的每个邻接点v for each vertex v∈Adj[u] // 更新v的当前最短路。 // 具体策略是:有一个从s到v的新路径,即“从s走全图最短路到u,再从u到v”。 // 这个新路径可能比v的当前最短路长,也可能比v的当前最短路短。(这个不那么显然,后续有说明) // 如果新路径比v的当前最短路短,就把v的当前最短路替换为这条新路径。 do RELAX(u, v, w)
初始时,S S S S = { v 0 } S=\{v_0\} S = { v 0 } v 0 v_0 v 0 0 0 0 U U U v 0 v_0 v 0 U = { 其 余 顶 点 } U=\{其余顶点\} U = { 其 余 顶 点 } v 0 v_0 v 0 U U U v i v_i v i ( v 0 , v i ) (v_0,v_i) ( v 0 , v i ) v 0 v_0 v 0 v i v_i v i ( v 0 , v i ) (v_0,v_i) ( v 0 , v i ) ∞ ∞ ∞
从 U U U v 0 v_0 v 0 v k v_k v k v k v_k v k S S S v 0 v_0 v 0 v k v_k v k
以 v k v_k v k U U U v 0 v_0 v 0 v i v_i v i v k v_k v k v k v_k v k v i v_i v i v k v_k v k
重复步骤 2 和 3,直到所有顶点都包含在 S S S
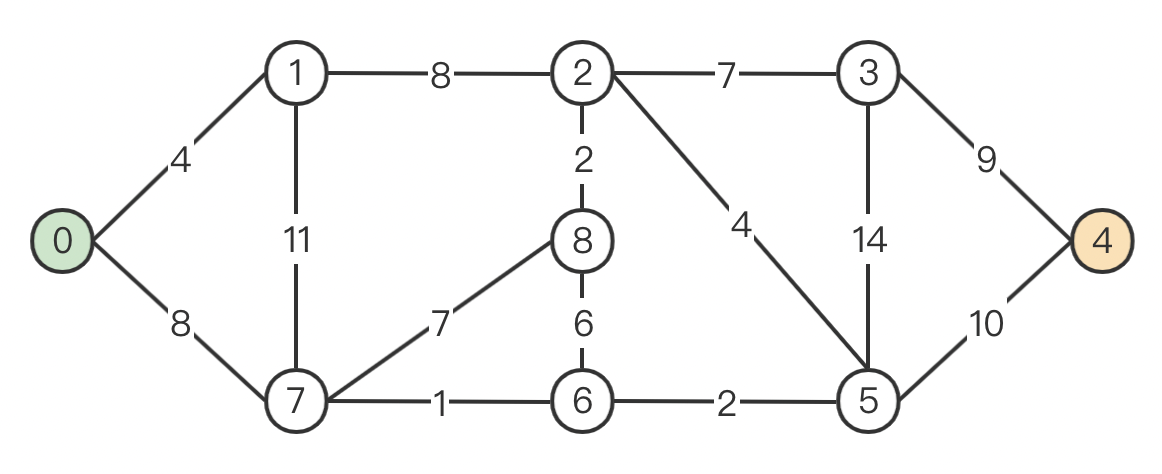
例:如下图所示,求出从 0 出发到 4 的最短路径。
【思路】 :
每次从没标记的节点中选择距离出发点最近的节点标记、收录到最优路径集合中;
计算刚加入的节点 A 到临近节点 B 的距离(不包含已标记节点),若 ( 节 点 A 的 距 离 + 节 点 A 到 节 点 B 的 距 离 ) < 节 点 B 的 距 离 (节点A的距离 + 节点A到节点B的距离) < 节点B的距离 ( 节 点 A 的 距 离 + 节 点 A 到 节 点 B 的 距 离 ) < 节 点 B 的 距 离
标记完所有的节点
【解】
将 [0] 放入集合:
0 [1]
2
3
4
5
6
7
8
dist
0
4
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ 8
∞ ∞ ∞
pred
\
0
\
\
\
\
\
0
\
将 [1] 放入集合:
0 1 2
3
4
5
6
[7]
8
dist
0
4
12
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ 8 ∗ 8^* 8 ∗ ∞ ∞ ∞
pred
\
0
1
\
\
\
\
0
\
注意⚠️:* 路径 0 → 1 → 7 0 \to 1 \to 7 0 → 1 → 7 4 + 11 = 15 4+11=15 4 + 1 1 = 1 5 0 → 7 0 \to 7 0 → 7 0 → 7 0 \to 7 0 → 7
将 [7] 放入集合:
0 1 2
3
4
5
[6]
7 8
dist
0
4
12
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ 9
8
15
pred
\
0
1
\
\
\
7
0
7
将 [6] 放入集合:
0 1 2
3
4
[5]
6 7 8
dist
0
4
12
∞ ∞ ∞ ∞ ∞ ∞ 11
9
8
15
pred
\
0
1
\
\
6
7
0
7
将 [5] 放入集合:
0 1 [2]
3
4
5 6 7 8
dist
0
4
12
25
21
11
9
8
15
pred
\
0
1
5
5
6
7
0
7
将 [2] 放入集合:
0 1 2 3
4
5 6 7 [8]
dist
0
4
12
19
21
11
9
8
14
pred
\
0
1
2
5
6
7
0
2
将 [8] 放入集合:由于与 8 相邻的节点都已经加入集合,所以可以跳过这一步
0 1 2 [3]
4
5 6 7 8
dist
0
4
12
19
21
11
9
8
14
pred
\
0
1
2
5
6
7
0
2
将 [3] 放入集合:
0 1 2 3 [4]
5 6 7 8
dist
0
4
12
19
21
11
9
8
14
pred
\
0
1
2
5
6
7
0
2
将 [4] 放入集合:
0 1 2 3 4 5 6 7 8
dist
0
4
12
19
21
11
9
8
14
pred
\
0
1
2
5
6
7
0
2
遍历完毕,我们现在就得到了从 0 到该图中所有点的最短路程 (shortest distance)。欲求出 0 → 4 0 \to 4 0 → 4
4 ← 5 ← 6 ← 7 ← 0 4 \leftarrow 5 \leftarrow 6 \leftarrow 7 \leftarrow 0
4 ← 5 ← 6 ← 7 ← 0
对于有向图 ,大体思路与无向图一致,注意边的方向即可,顺方向为可达,逆方向为不可达(即 ∞ ∞ ∞
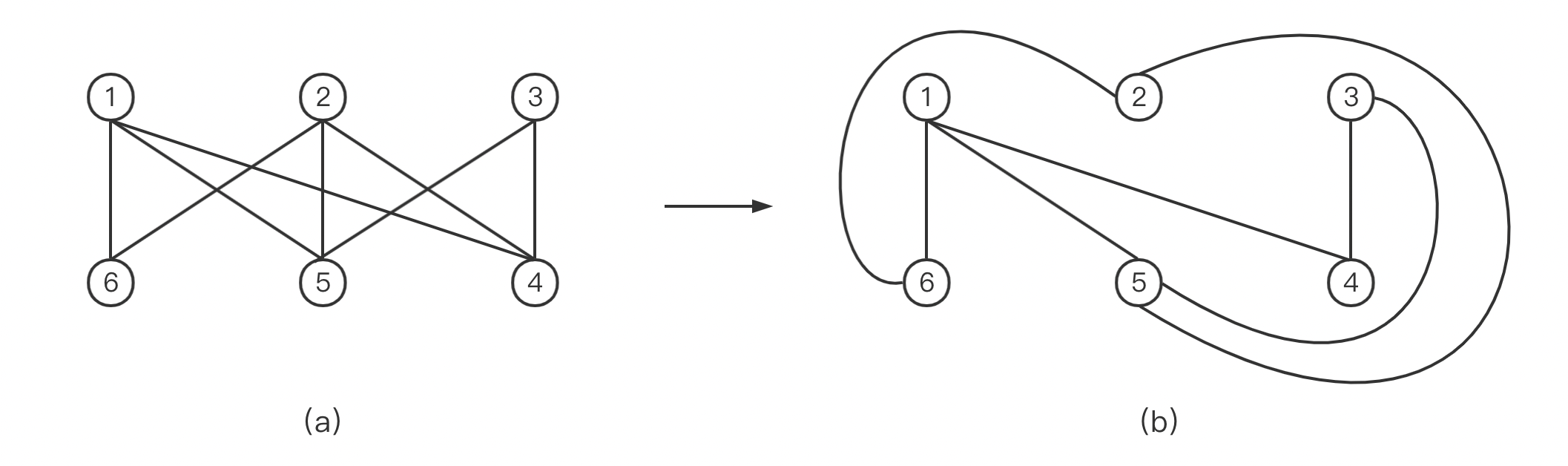
如下图,如果一个图 G G G 平面上 绘制,并且其边不相交 (边不一定是直线),则称该图是平面图 。
平面图所在的特定平面称为地图(carte);
将地图划分为几个区域称为面(face);
内部面:每个区域内部连同边界称为 G G G
外部面:无界的区域
注:每个平面图有且仅有一个外部面。
而如果一个图无论怎样都无法画在平面上,并使得不同的边互不交叠,那么这样的图不是平面图,或者称为非平面图。
完全图 K 5 K_5 K 5 K 3 , 3 K_{3,3} K 3 , 3
面的次数:设 f f f G G G f f f 边界的边数 (割边算两次)称为 f f f 次数 , 记作 d e g ( f ) deg(f) d e g ( f )
这实际上是一个研究图的拓扑方面的问题。 更一般地,人们可以问一个图形是否可以在表面 S 上表示的问题
设 G G G n n n m m m f f f p p p 连通分支 (composantes connexes) 的平面图,则:
f = m − n + 1 + p 即 面 数 = 边 数 − 顶 点 数 + 1 + 连 通 部 分 的 数 量 f = m-n+1+p \quad 即 \quad 面数=边数-顶点数+1+连通部分的数量
f = m − n + 1 + p 即 面 数 = 边 数 − 顶 点 数 + 1 + 连 通 部 分 的 数 量
【欧拉示性数 (Euler characteristic)】 :具有 n n n m m m f f f 连通平面图 G G G
n − m + f = 2 , 即 顶 点 数 − 边 数 + 面 数 = 2 n-m+f=2,\quad 即 \quad 顶点数-边数+面数=2
n − m + f = 2 , 即 顶 点 数 − 边 数 + 面 数 = 2
【推论】具有 n n n m m m n ≥ 3 n \ge 3 n ≥ 3 m ≤ 3 n − 6 m \le 3n -6 m ≤ 3 n − 6
【定义】设 G G G G G G 任意两个不相邻的顶点 之间添加一条边所得到的图均为不可平面图 ,则称该图 G G G
(必要条件)G G G G G G G G G G G G
设 G G G G G G 充要条件 是 G G G 各个面的次数均为3 且 为简单图
设 G G G n n n m m m f f f m = 3 n − 6 m=3n-6 m = 3 n − 6 f = 2 n − 4 f =2n-4 f = 2 n − 4
【独立集】(Independent ensemble)是图论中的概念。一个独立集(也称为稳定集 stable ensemble)是一个图中一些两两不相邻的顶点所形成的集合 。换句话说,独立集 S S S S S S α ( G ) \alpha (G) α ( G )
【着色】在一个图 G G G 相邻的两个顶点不能着相同的颜色 (即一条边两端的顶点不能着相同的颜色;也即当一个图的顶点可分为 n n n n n n γ ( G ) \gamma (G) γ ( G )
如果一个图所需颜色 γ ( G ) \gamma (G) γ ( G ) k k k k − 点 可 着 色 的 k-点可着色的 k − 点 可 着 色 的
常见的图的着色所需颜色的数量:
γ ( K p ) = p \gamma (K_p) = p γ ( K p ) = p γ ( 具 有 2 n 个 顶 点 的 环 ) = 2 \gamma (具有2n个顶点的环) = 2 γ ( 具 有 2 n 个 顶 点 的 环 ) = 2 γ ( 具 有 2 n + 1 个 顶 点 的 环 ) = 3 \gamma (具有2n+1个顶点的环) = 3 γ ( 具 有 2 n + 1 个 顶 点 的 环 ) = 3 γ ( T r e e ) = 2 \gamma (Tree) = 2 γ ( T r e e ) = 2
例:
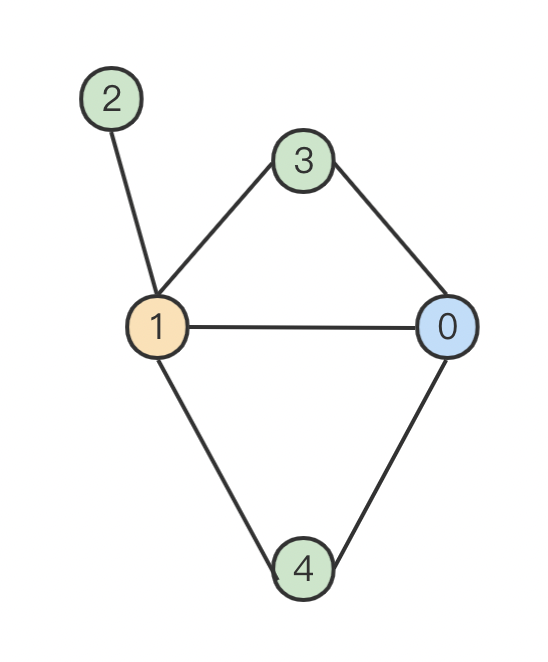
上图 G G G { 0 } , { 1 } , { 2 , 3 , 4 } \{0\},\quad \{1\}, \quad \{2,3,4\} { 0 } , { 1 } , { 2 , 3 , 4 }
α ( G ) = 3 \alpha (G) = 3 α ( G ) = 3 γ ( G ) = 3 \gamma (G) = 3 γ ( G ) = 3
γ ( G ) ≥ n b ( V ) n b ( V ) − m i n v ∈ V δ ( v ) \gamma (G) \ge \frac {nb(V)}{nb(V) - min_{v \in V} \delta(v)}
γ ( G ) ≥ n b ( V ) − m i n v ∈ V δ ( v ) n b ( V )
其中,
m i n v ∈ V δ ( v ) min_{v \in V} \delta(v) m i n v ∈ V δ ( v ) G G G 拥有最小度的顶点 v v v ,即 在一个图中,拥有最少相邻顶点的顶点 v v v
n b ( V ) − m i n v ∈ V δ ( v ) − 1 nb(V) - min_{v \in V} \delta(v) - 1 n b ( V ) − m i n v ∈ V δ ( v ) − 1 v v v 不邻接的顶点数 ,而此时就可以知道最多的同色顶点数 是 n b ( V ) − m i n v ∈ V δ ( v ) nb(V) - min_{v \in V} \delta(v) n b ( V ) − m i n v ∈ V δ ( v )
总共色数是 γ ( G ) \gamma (G) γ ( G ) n b ( V ) − m i n v ∈ V δ ( v ) nb(V) - min_{v \in V} \delta(v) n b ( V ) − m i n v ∈ V δ ( v ) 小于等于 顶点数 n b ( V ) nb(V) n b ( V ) γ ( G ) × n b ( V ) − m i n v ∈ V δ ( v ) ≤ n b ( V ) \gamma (G) \times nb(V) - min_{v \in V} \delta(v) \le nb(V) γ ( G ) × n b ( V ) − m i n v ∈ V δ ( v ) ≤ n b ( V )
整理可得出上式
γ ( G ) ≥ # ( 最 大 团 ( c l i q u e ) 中 的 顶 点 数 ) \gamma (G) \ge \#(最大团_{(clique)}中的顶点数)
γ ( G ) ≥ # ( 最 大 团 ( c l i q u e ) 中 的 顶 点 数 )
γ ( G ) ≤ m a x v ∈ V δ ( v ) + 1 \gamma (G) \le max_{v \in V} \delta(v) + 1
γ ( G ) ≤ m a x v ∈ V δ ( v ) + 1
其中,
m a x v ∈ V δ ( v ) max_{v \in V} \delta(v) m a x v ∈ V δ ( v ) G G G 拥有最大度的顶点 v v v ,也可写作 Δ ( G ) \Delta (G) Δ ( G ) v v v
证明:(数学归纳法)
当 n = 1 或 2 n=1或2 n = 1 或 2
假设有 p p p p + 1 p+1 p + 1 v i v_i v i G G G v i v_i v i G G G G 1 G_1 G 1 G 1 G_1 G 1 p p p G 1 G_1 G 1 G G G G 1 G_1 G 1 G G G
γ ( G 1 ) ≤ Δ ( G 1 ) + 1 ≤ Δ ( G ) + 1 \gamma (G_1)\quad \le \quad\Delta (G_1) + 1 \quad \le \quad\Delta (G) + 1
γ ( G 1 ) ≤ Δ ( G 1 ) + 1 ≤ Δ ( G ) + 1
当将 G 1 G_1 G 1 G G G v v v G 1 G_1 G 1 Δ ( G ) \Delta (G) Δ ( G ) G 1 G_1 G 1 Δ ( G ) \Delta (G) Δ ( G ) Δ ( G ) \Delta (G) Δ ( G ) Δ ( G ) + 1 \Delta (G) + 1 Δ ( G ) + 1 v v v v v v
Proof:
We use induction on the number of vertices in the graph, which we denote by n n n P ( n ) P(n) P ( n ) n-vertex graph with maximum degree Δ ( G ) \Delta(G) Δ ( G ) k k k ( k + 1 ) (k + 1) ( k + 1 )
Base case (n = 1):
A 1-vertex graph has maximum degree 0 0 0 1-colorable, so P ( 1 ) P (1) P ( 1 )
Inductive step:
Now assume that P ( n ) P (n) P ( n ) G G G (n + 1)-vertex graph with maximum degree Δ ( G ) \Delta(G) Δ ( G ) k k k
Remove a vertex v v v n-vertex subgraph, H H H H H H Δ H \Delta H Δ H k k k H H H (k + 1)-colorable by our assumption P ( n ) P (n) P ( n )
Now add back vertex v v v v v v k + 1 k + 1 k + 1 adjacent vertices , since there are at most k k k v v v k + 1 k + 1 k + 1
Therefore, G G G (k + 1)-colorable. This completes the inductive step, and the theorem follows by induction .
【Brooks定理】
设连通图即不是完全图 K n ( n ≥ 3 ) K_n(n \ge 3) K n ( n ≥ 3 )
γ ( G ) ≤ Δ ( G ) \gamma (G) \le \Delta (G)
γ ( G ) ≤ Δ ( G )
γ ( G ) ≤ n + 1 − α ( G ) \gamma (G) \le n + 1 - \alpha(G)
γ ( G ) ≤ n + 1 − α ( G )
在一个图 G G G 相邻的两个边不能着相同的颜色 (即与同一个顶点链接的边不能着相同的颜色)。我们用 γ ( G ) \gamma (G) γ ( G )
如果一个图对边着色所需颜色 γ ′ ( G ) \gamma' (G) γ ′ ( G ) k k k k − 边 可 着 色 的 k-边可着色的 k − 边 可 着 色 的
【性质】(维津定理)设G是简单图,则
Δ ( G ) ≤ γ ′ ( G ) ≤ Δ ( G ) + 1 \Delta (G) \le \gamma'(G) \le \Delta (G) +1
Δ ( G ) ≤ γ ′ ( G ) ≤ Δ ( G ) + 1
连通的无桥 平面图的平面嵌入及其所有的面称为平面地图 或地图 ,平面地图的面称为国家 。若两个国家的边界至少有一条公共边,则称这两个国家是相邻 的。
在一个平面地图 G G G 相邻的两个面不能着相同的颜色 。我们用 γ ∗ ( G ) \gamma^* (G) γ ∗ ( G )
如果一个地图所需颜色 γ ∗ ( G ) \gamma^* (G) γ ∗ ( G ) k k k k − 面 可 着 色 的 k-面可着色的 k − 面 可 着 色 的
【定理】地图 G G G k − 面 可 着 色 的 k-面可着色的 k − 面 可 着 色 的 G ∗ G^* G ∗ k − 点 可 着 色 的 k-点可着色的 k − 点 可 着 色 的
【五色定理】任何一个平面图都是 5 − 面 可 着 色 的 5-面可着色的 5 − 面 可 着 色 的
证明:
回顾第二部分的连通部分
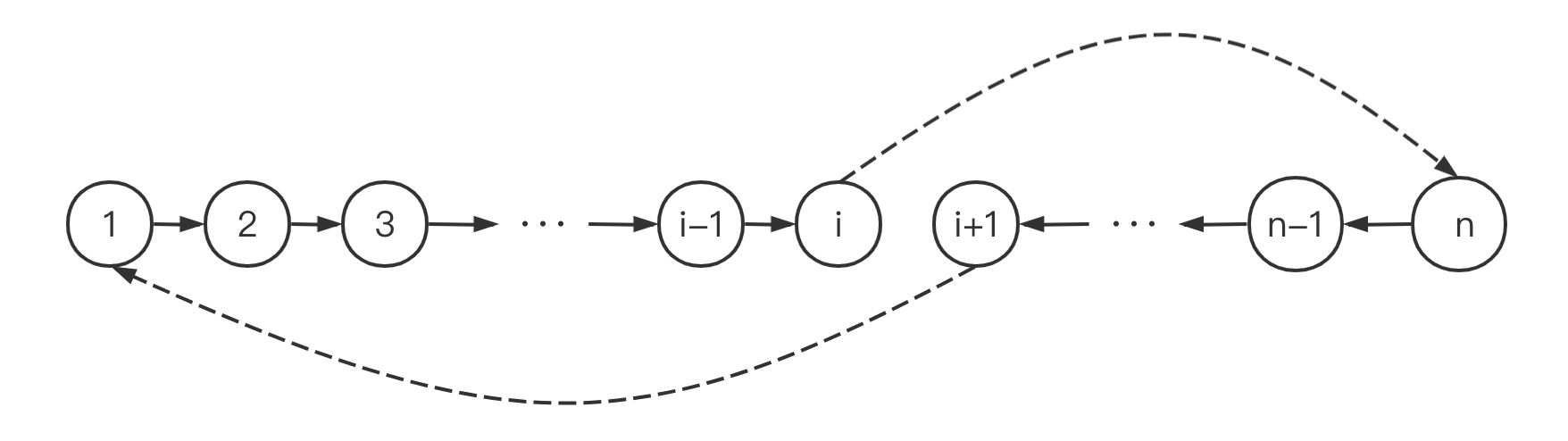
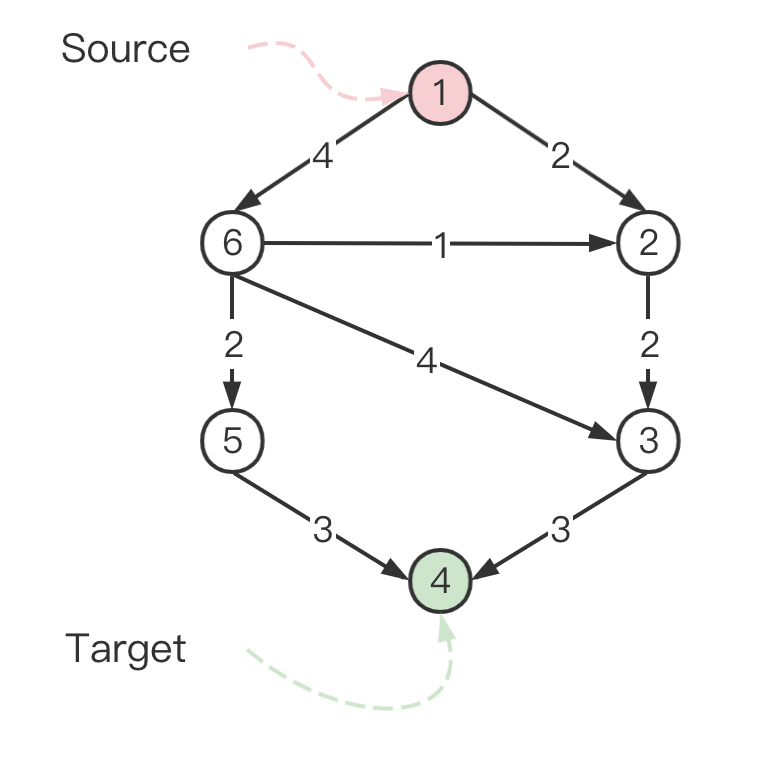
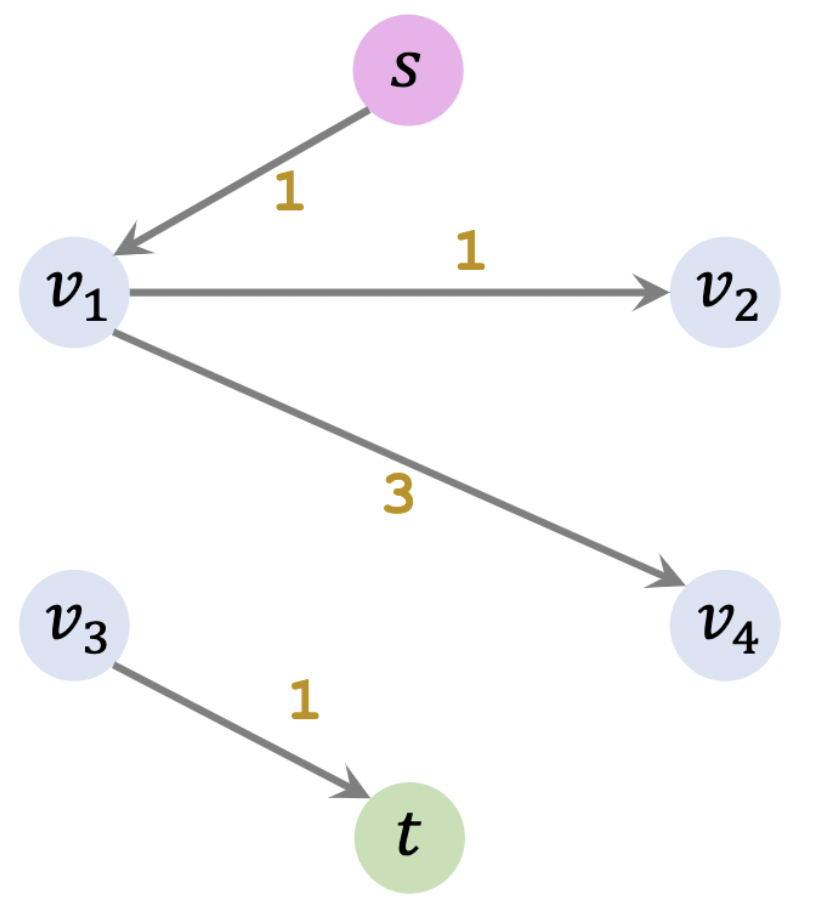
在生活中,经常会遇到一类问题:我们有一个如上图所示的抽象的供水管网,有起点和终点,我们需要求解关于这个供水管网的一系列性能问题。那么我们可以将其网络模型视为一种有向图 D D D
D = ( V , E , ω ) D=(V,E,\omega)
D = ( V , E , ω )
其中:
s , t ∈ V s,t \in V s , t ∈ V s s s t t t ω \omega ω A → R A \to R A → R x ∈ A x \in A x ∈ A ω ( x ) \omega (x) ω ( x ) x x x
【名词解释】
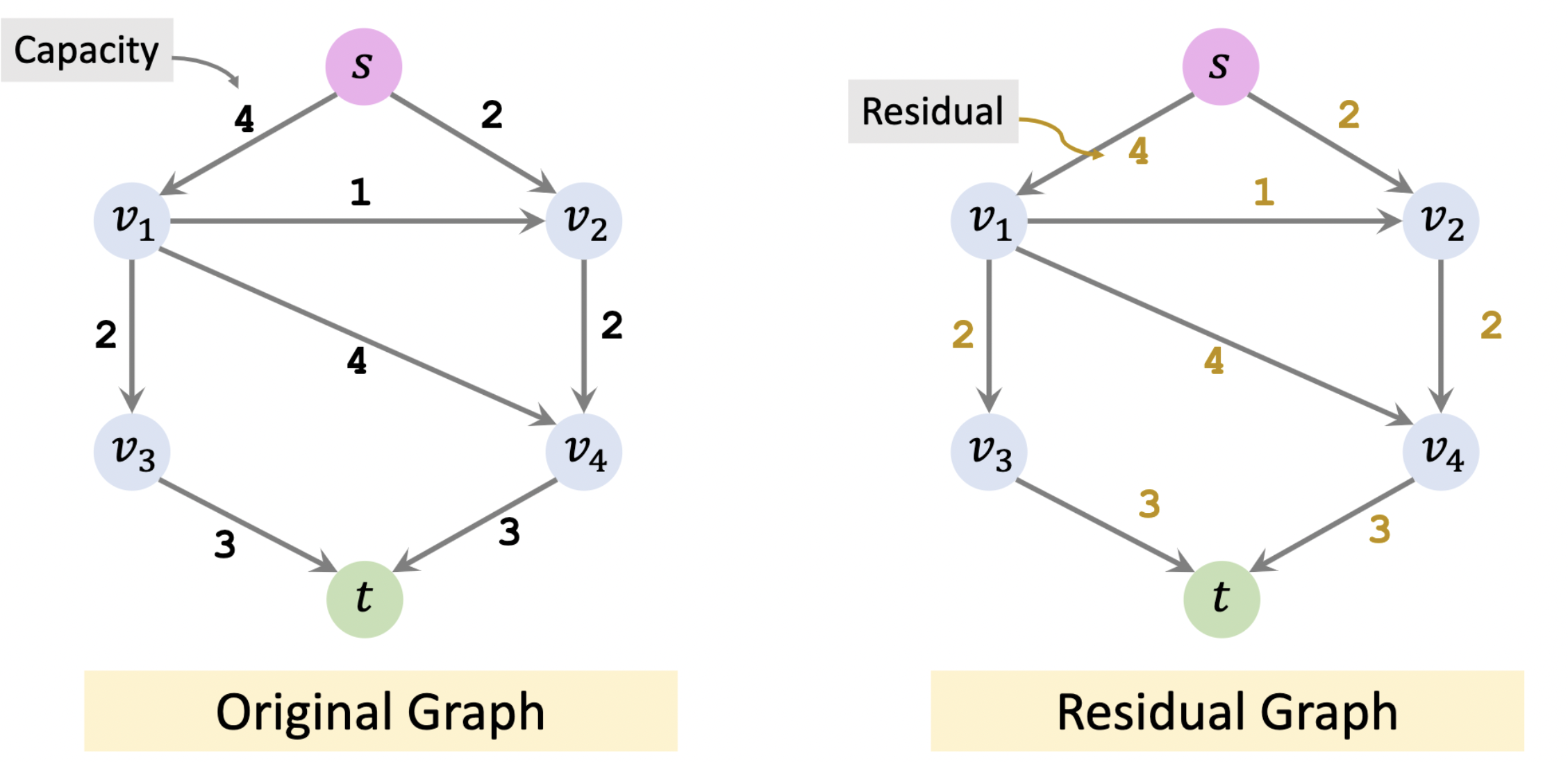
流量 (Flow):实际 在模型中管线里的流量 ,流量不能超过容量
容量 (Capacity):模型中边的权重,为该条边 所能够承受的最大流量
残差 (Residual):又称空闲量,指“该条边在当前流量下还可以继续承受的流量”,即 R e s i d u a l = C a p a c i t y − F l o w R_{esidual} = C_{apacity} - F_{low} R e s i d u a l = C a p a c i t y − F l o w
最大流 (Maximum Flow):在当前模型中能流过的最大总流量
最小割
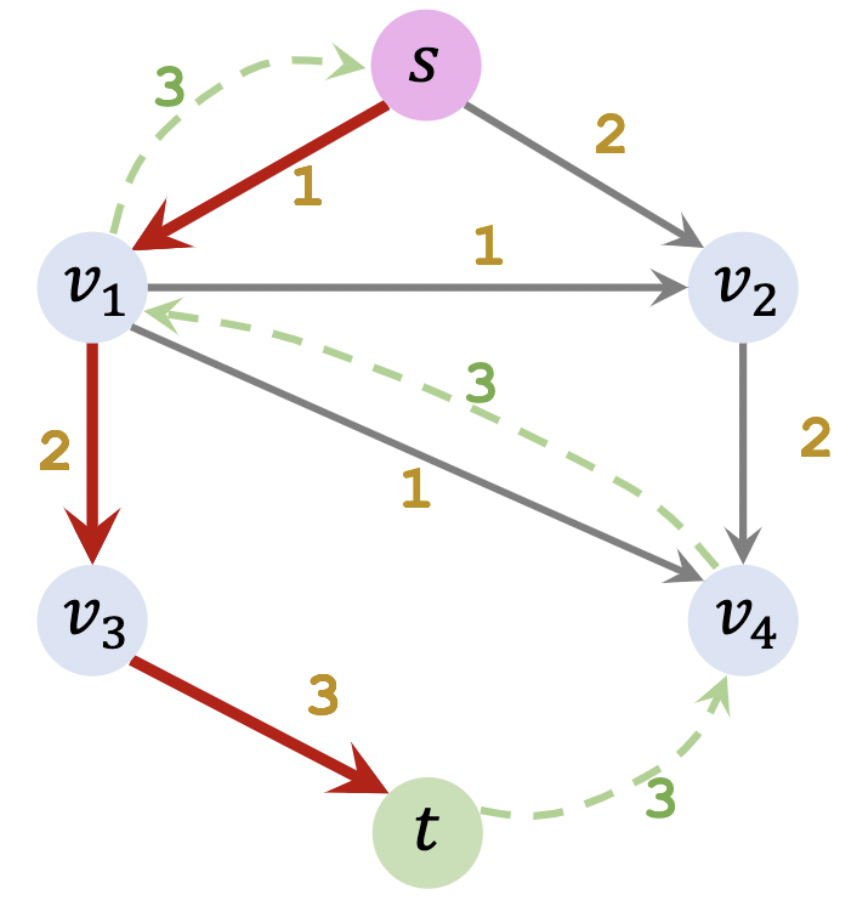
我们根据原图 (左) 创建一个残差图 (右),其中空闲量 R e s i d u a l = C a p a c i t y − F l o w R_{esidual} = C_{apacity} - F_{low} R e s i d u a l = C a p a c i t y − F l o w F l o w F_{low} F l o w 0 0 0
【第一轮循环】
节点
v 1 v_1 v 1 v 2 v_2 v 2 v 4 v_4 v 4 t
[前序,方向,权重]
[s,+,4]
[S,+,2]
[v 2 v_2 v 2
[v 4 v_4 v 4
我们在残差图中找出一条从起点 s s s t t t 2 2 2 − 2 -2 − 2
当某一条边的饱和 (Staturated) 即残差量为 0 0 0 移除 。第一轮循环结束。
【第二轮循环】
节点
v 1 v_1 v 1 v 4 v_4 v 4 v 3 v_3 v 3 t
[前序,方向,权重]
[s,+,4]
[v 1 v_1 v 1
[v 1 v_1 v 1
[v 3 v_3 v 3
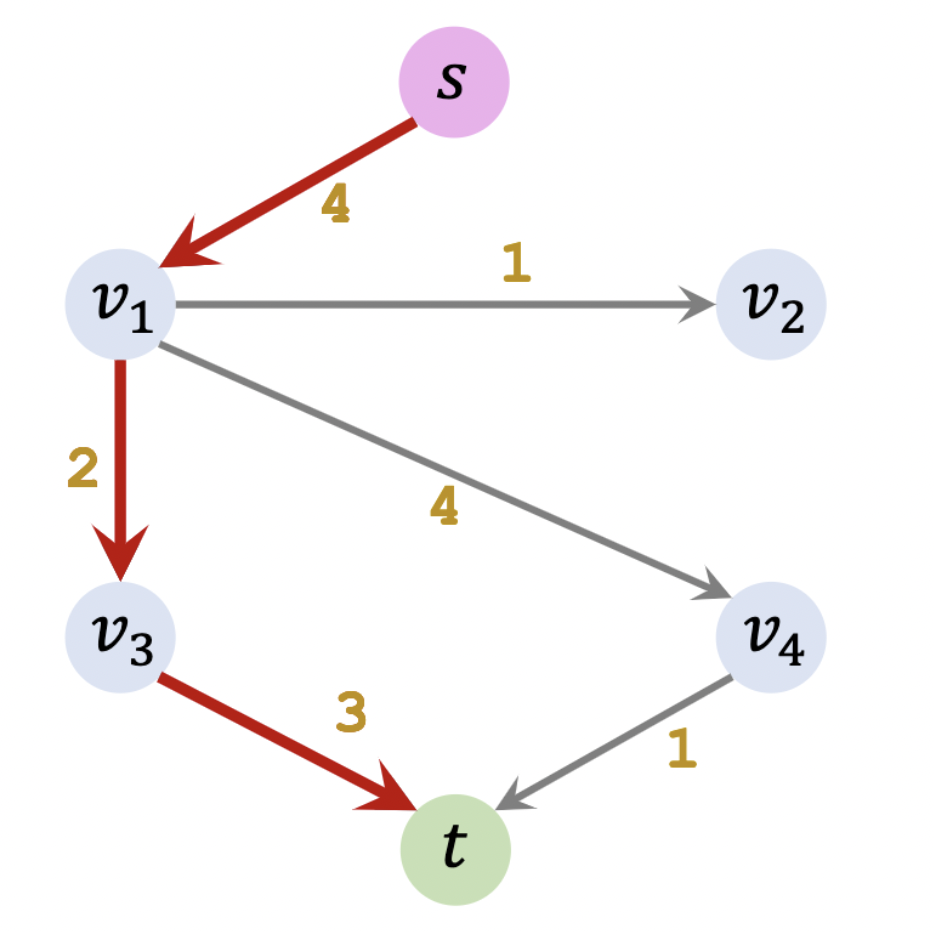
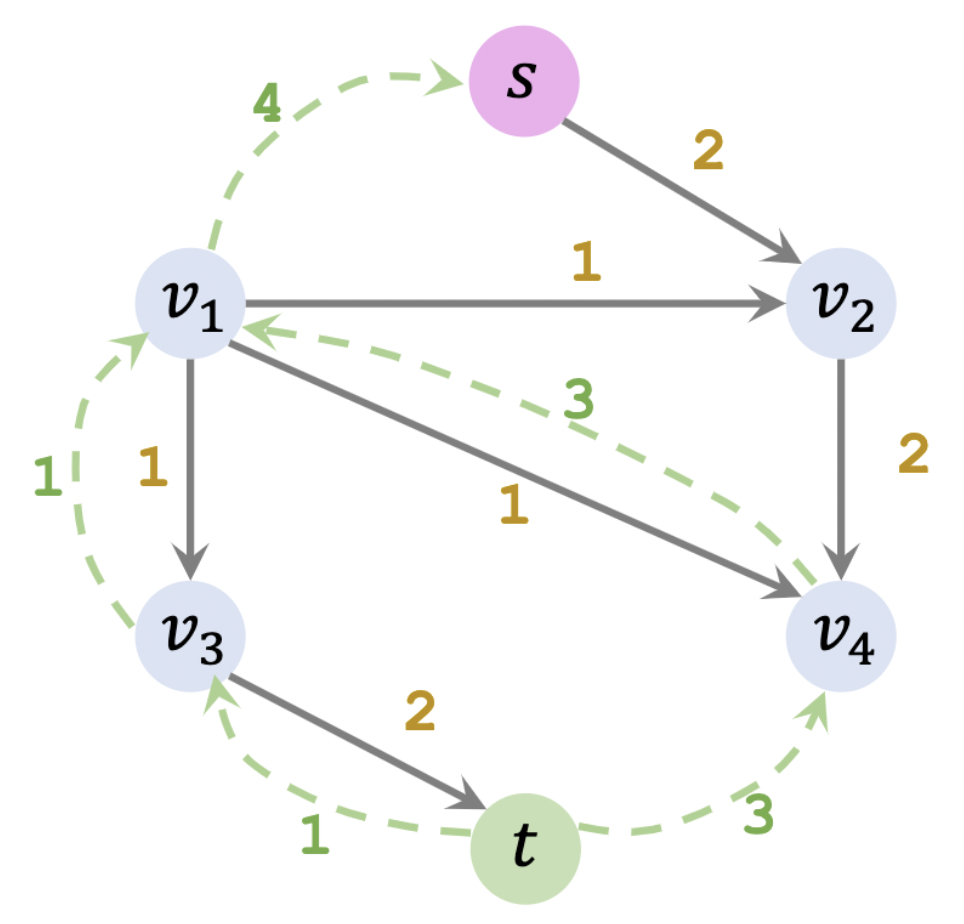
如下图所示,我们找到了一条从起点 s s s t t t
由于短板效应,该条路径最多只能输送 2 2 2 − 2 -2 − 2
【第三次循环】
节点
v 1 v_1 v 1 v 4 v_4 v 4 t
[前序,方向,权重]
[s,+,2]
[v 1 v_1 v 1
[v 4 v_4 v 4
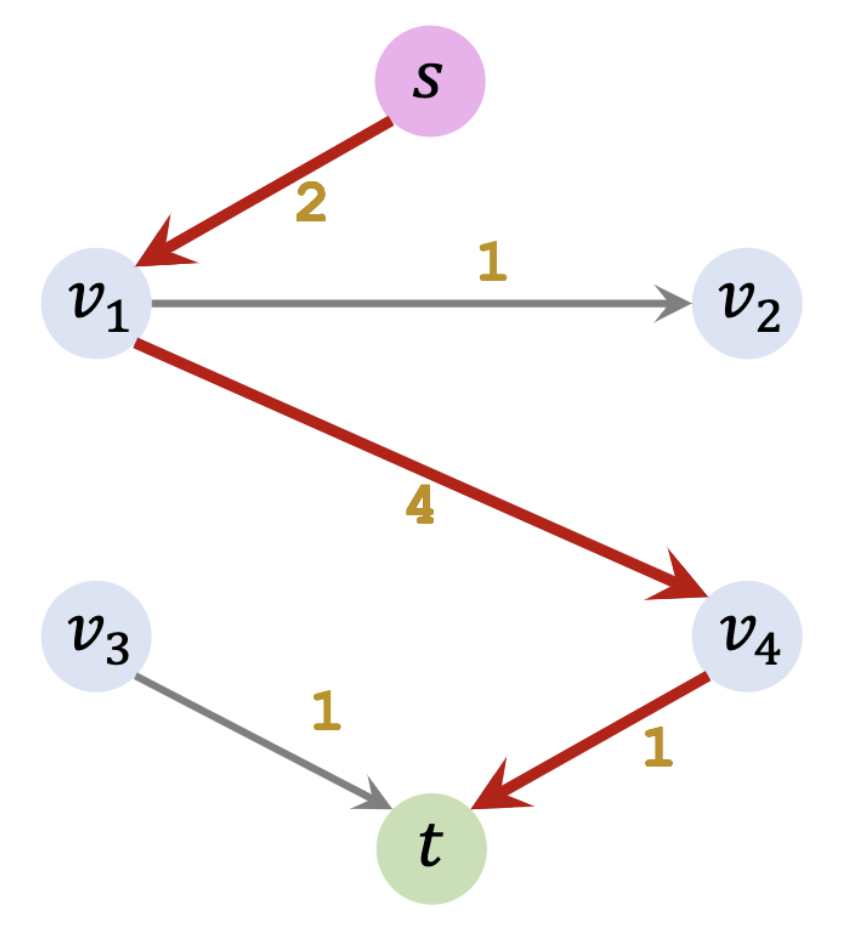
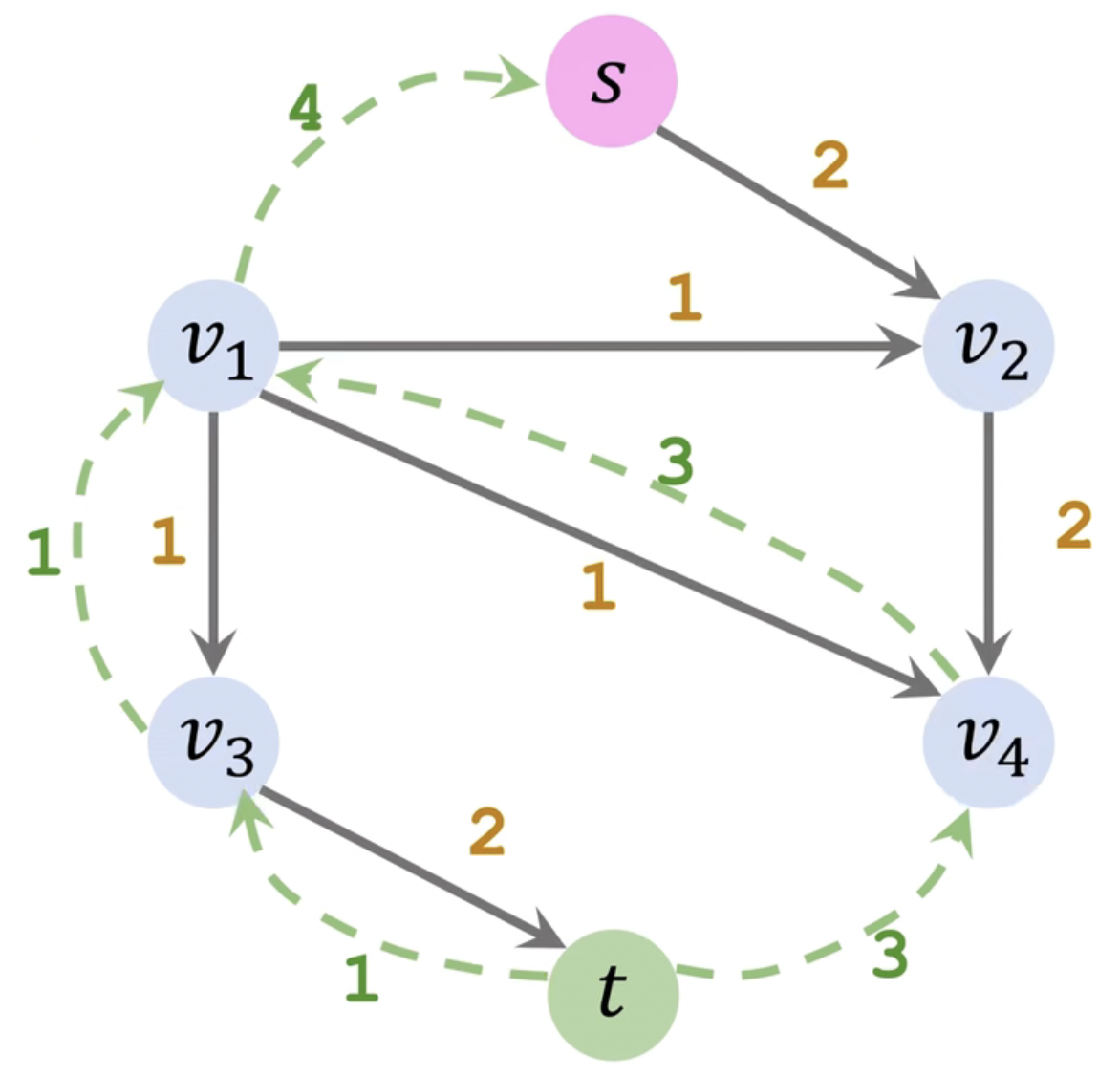
如下图所示,我们找到了一条从起点 s s s t t t
由于短板效应,该条路径最多只能输送 1 1 1 − 1 -1 − 1
【第四次循环】
节点
v 1 v_1 v 1 v 2 v_2 v 2 v 4 v_4 v 4 t
[前序,方向,权重]
[s,+,1]
[v 1 v_1 v 1
[v 1 v_1 v 1
[v 3 v_3 v 3
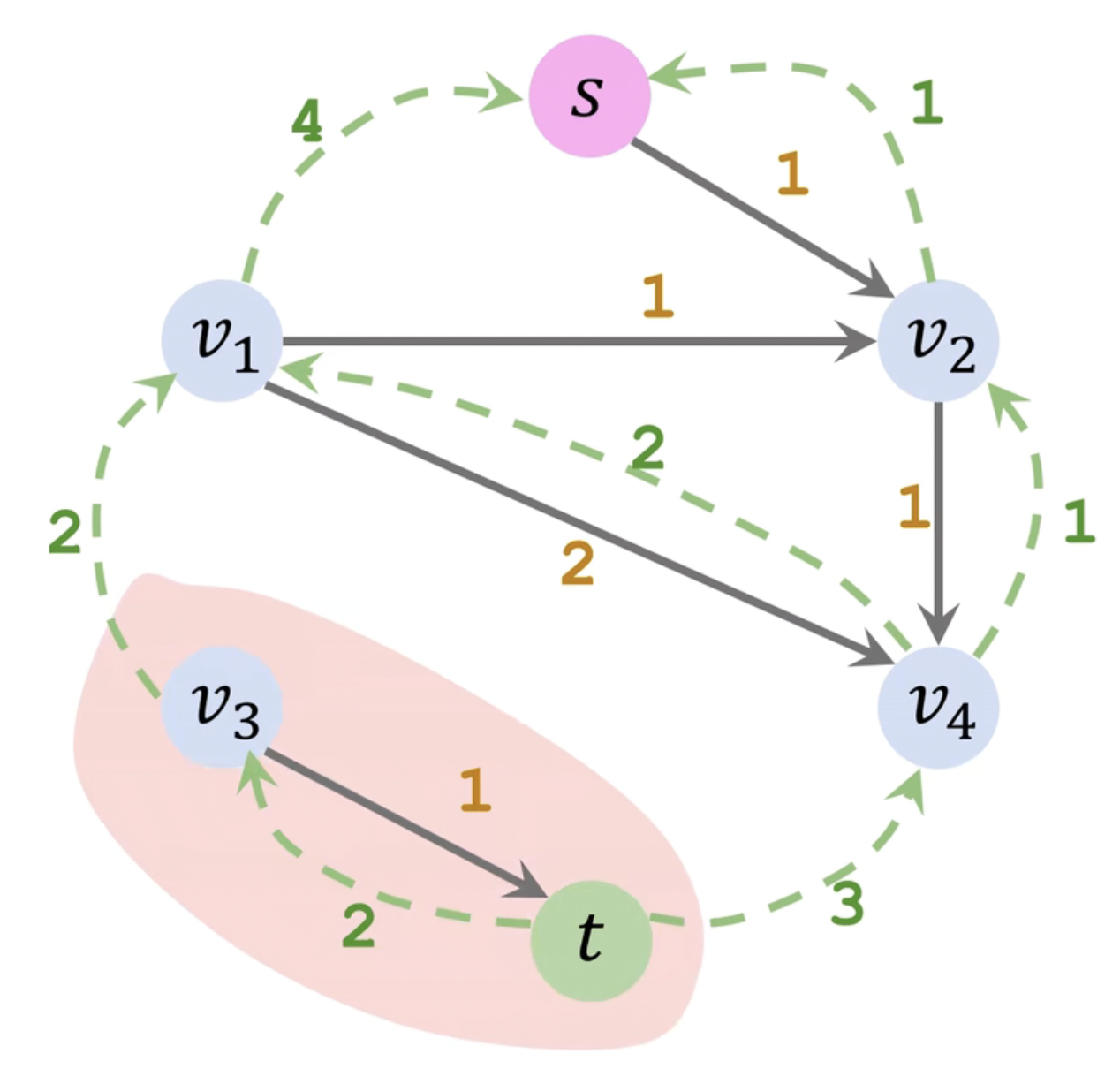
如下图所示,我们无法找到 一条从起点 s s s t t t
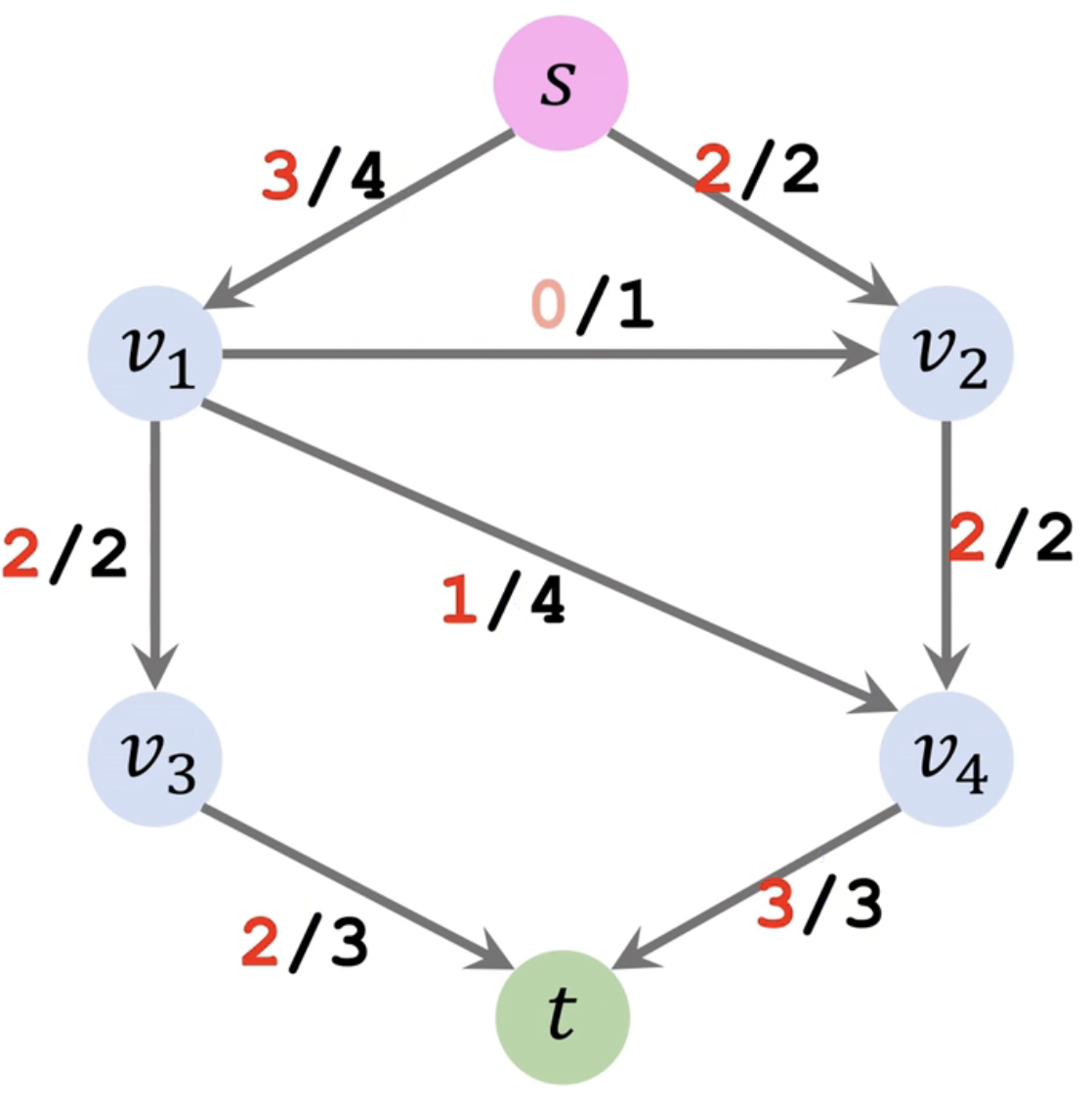
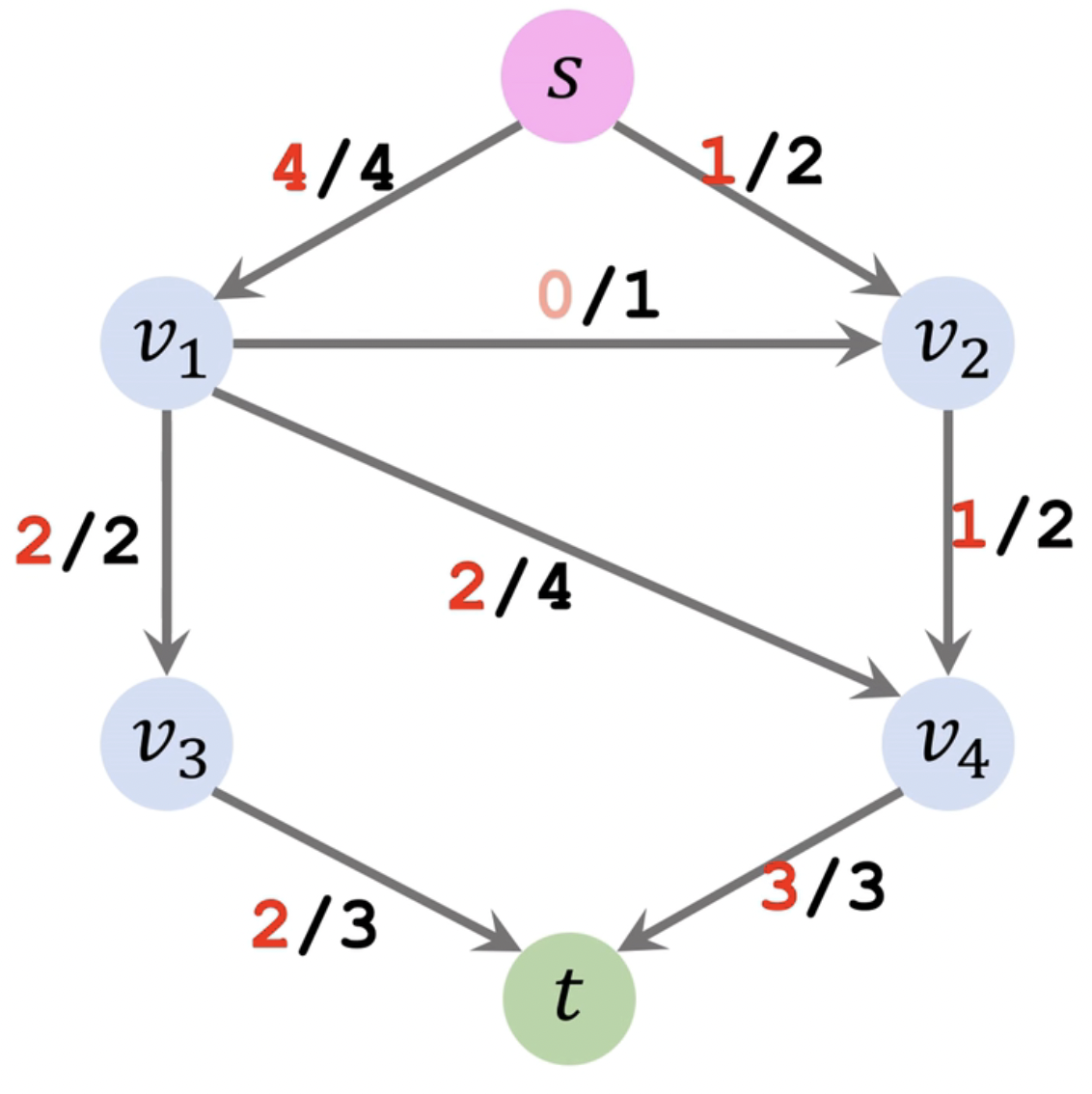
用最后一次循环结果更新的残差 (Residual) 图与原图 (Capacity) 比较,得出流量 (Flow) 图,即 F l o w = C a p a c i t y − R e s i d u a l F_{low} = C_{apacity} - R_{esidual} F l o w = C a p a c i t y − R e s i d u a l
其中,边上的权重为 [ F l o w / C a p a c i t y ] [F_{low}/C_{apacity}] [ F l o w / C a p a c i t y ] = 2 + 3 = 5 = 2+3 = 5 = 2 + 3 = 5
Ford-Fulkerson 算法一定能找到最大流,其与之前的简单算法的区别是:添加了一个回溯路径 ,一旦选择了“不好的”路径,就会撤销这个路径,沿着回溯路径回到源点。
【算法描述】
我们根据原图 (左) 创建一个残差图 (右),其中空闲量 R e s i d u a l = C a p a c i t y − F l o w R_{esidual} = C_{apacity} - F_{low} R e s i d u a l = C a p a c i t y − F l o w F l o w F_{low} F l o w 0 0 0
【第一轮循环】
节点
v 1 v_1 v 1 v 2 v_2 v 2 v 4 v_4 v 4 t
[前序,方向,权重]
[s,+,4]
[S,+,2]
[v 1 v_1 v 1
[v 4 v_4 v 4
backtracking path (next)
[S,-,0]
[S,-,0]
[v 1 v_1 v 1
[v 4 v_4 v 4
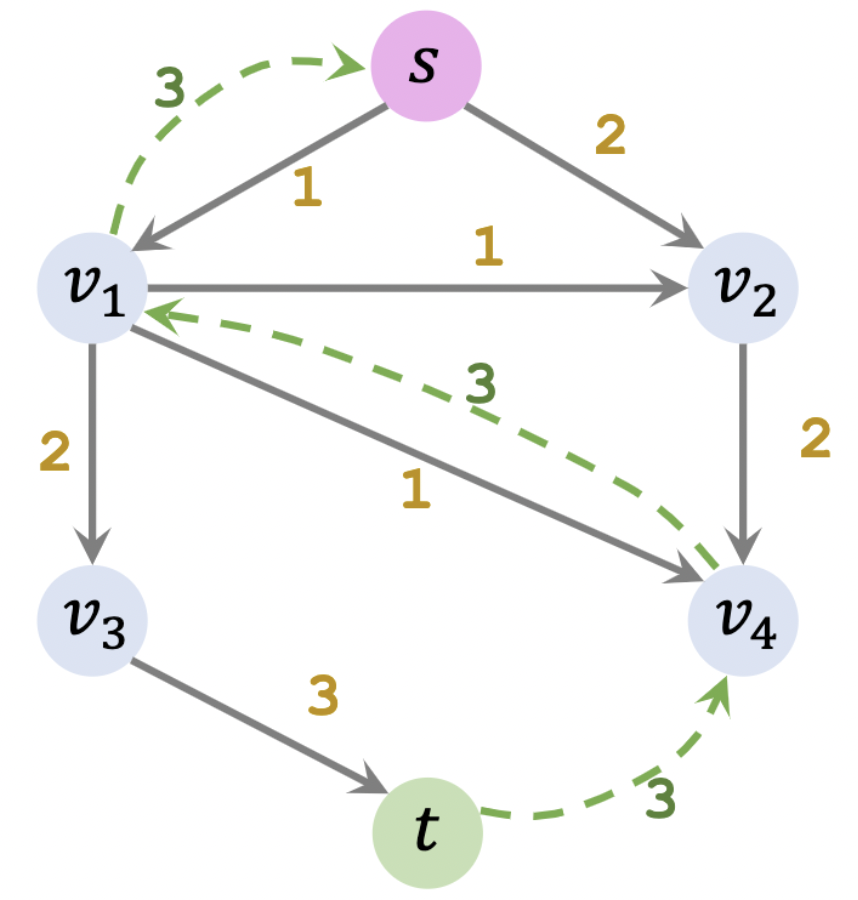
我们在残差图中找出一条从起点 s s s t t t 3 3 3 − 3 -3 − 3
如上图所示,添加一条绿色的回溯路径 ,每个边的权都为 3 3 3 t ⟶ 3 v 4 ⟶ 3 v 1 ⟶ 3 s t \stackrel{3}\longrightarrow v_4\stackrel{3}\longrightarrow v_1 \stackrel{3}\longrightarrow s t ⟶ 3 v 4 ⟶ 3 v 1 ⟶ 3 s
【第二轮循环】
节点
v 1 v_1 v 1 v 2 v_2 v 2 v 3 v_3 v 3 t
[前序,方向,权重]
[S,+,1]
[S,+,2]
[v 1 v_1 v 1
[v 3 v_3 v 3
backtracking path
[S,-,3]
[S,-,0]
[v 1 v_1 v 1
[v 3 v_3 v 3
如下图所示,我们找到了一条从起点 s s s t t t
由于短板效应,该条路径最多只能输送 1 1 1 − 1 -1 − 1
如上图所示,添加一条绿色的回溯路径 ,每个边的权都为 1 1 1 t ⟶ 1 v 3 ⟶ 1 v 1 ⟶ 1 s t \stackrel{1}\longrightarrow v_3\stackrel{1}\longrightarrow v_1 \stackrel{1}\longrightarrow s t ⟶ 1 v 3 ⟶ 1 v 1 ⟶ 1 s
【第三轮循环】
节点
v 1 v_1 v 1 v 2 v_2 v 2 v 4 v_4 v 4 v 3 v_3 v 3 t
[前序,方向,权重]
[S,+,0]
[S,+,2]
[v 2 v_2 v 2 v 1 v_1 v 1
[v 1 v_1 v 1
[v 3 v_3 v 3
backtracking path
[S,-,4]
[S,-,0]
[v 2 v_2 v 2 v 1 v_1 v 1
[v 1 v_1 v 1
[v 3 v_3 v 3
如果此时我们将绿色的回溯路径去掉,我们就不能在起点和终点之间找到一条路径。Ford-Fulkerson 算法的关键就在于这些回溯路径。如下图所示,我们考虑回溯路径,我们找到了一条从起点 s s s t t t s ⟶ 2 v 2 ⟶ 2 v 4 ⟶ 3 ∗ v 1 ⟶ 1 v 3 ⟶ 2 t s \stackrel{2}\longrightarrow v_2 \stackrel{2}\longrightarrow v_4 \stackrel{3^*}\longrightarrow v_1 \stackrel{1}\longrightarrow v_3 \stackrel{2}\longrightarrow t s ⟶ 2 v 2 ⟶ 2 v 4 ⟶ 3 ∗ v 1 ⟶ 1 v 3 ⟶ 2 t
由于短板效应,该条路径最多只能输送 1 1 1 − 1 -1 − 1 s ⟶ 1 v 2 ⟶ 1 v 4 ⟶ 2 ∗ v 1 ⟶ 0 v 3 ⟶ 1 t s \stackrel{1}\longrightarrow v_2 \stackrel{1}\longrightarrow v_4 \stackrel{2^*}\longrightarrow v_1 \stackrel{0}\longrightarrow v_3 \stackrel{1}\longrightarrow t s ⟶ 1 v 2 ⟶ 1 v 4 ⟶ 2 ∗ v 1 ⟶ 0 v 3 ⟶ 1 t
如上图所示,添加一条绿色的回溯路径 ,每个边的权都为 1 1 1 t ⟶ 1 v 3 ⟶ 1 v 1 ⟶ 1 ∗ v 4 ⟶ 1 v 2 ⟶ 1 s t \stackrel{1}\longrightarrow v_3 \stackrel{1}\longrightarrow v_1 \stackrel{1^*}\longrightarrow v_4 \stackrel{1}\longrightarrow v_2 \stackrel{1}\longrightarrow s t ⟶ 1 v 3 ⟶ 1 v 1 ⟶ 1 ∗ v 4 ⟶ 1 v 2 ⟶ 1 s
【第四轮循环】
如第三轮循环末的图所示,没有任何路径通往红色区域 v 3 ⟶ 1 t v_3 \stackrel{1}\longrightarrow t v 3 ⟶ 1 t
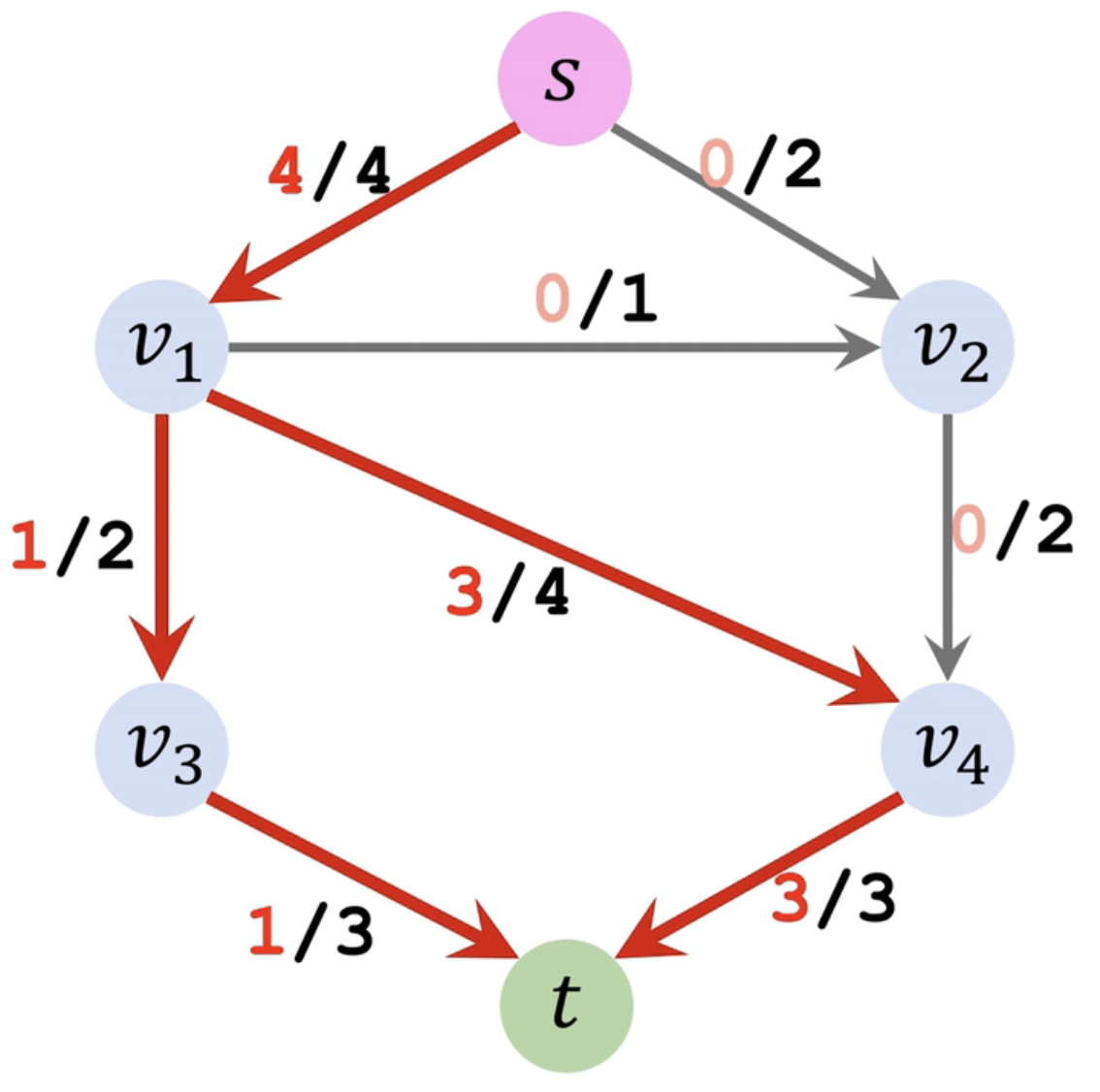
用最后一次循环结果更新的残差 (Residual) 图去除所有回溯路径 与原图 (Capacity) 比较,得出流量 (Flow) 图,即 F l o w = C a p a c i t y − R e s i d u a l F_{low} = C_{apacity} - R_{esidual} F l o w = C a p a c i t y − R e s i d u a l
其中,边上的权重为 [ F l o w / C a p a c i t y ] [F_{low}/C_{apacity}] [ F l o w / C a p a c i t y ] = 2 + 3 = 5 = 2+3 = 5 = 2 + 3 = 5 5 5 5
我们先回顾一下之前之前学习的割,可类比与今天的网络流中最小割问题。
在如上图所示的网络流中,有向图 D = ( V , E , ω ) D=(V,E,\omega) D = ( V , E , ω )
其中:
s , t ∈ V s,t \in V s , t ∈ V s s s t t t ω \omega ω A → R A \to R A → R x ∈ A x \in A x ∈ A ω ( x ) \omega (x) ω ( x ) x x x
【定义】S-T Cut:将所有的顶点分为两个集合 S S S T T T
S ∪ P = V S \cup P = V S ∪ P = V S ∩ P = ∅ S \cap P = \emptyset S ∩ P = ∅ s ∈ S s \in S s ∈ S t ∈ T t \in T t ∈ T 二元组集合 ( S , T ) (S,T) ( S , T )
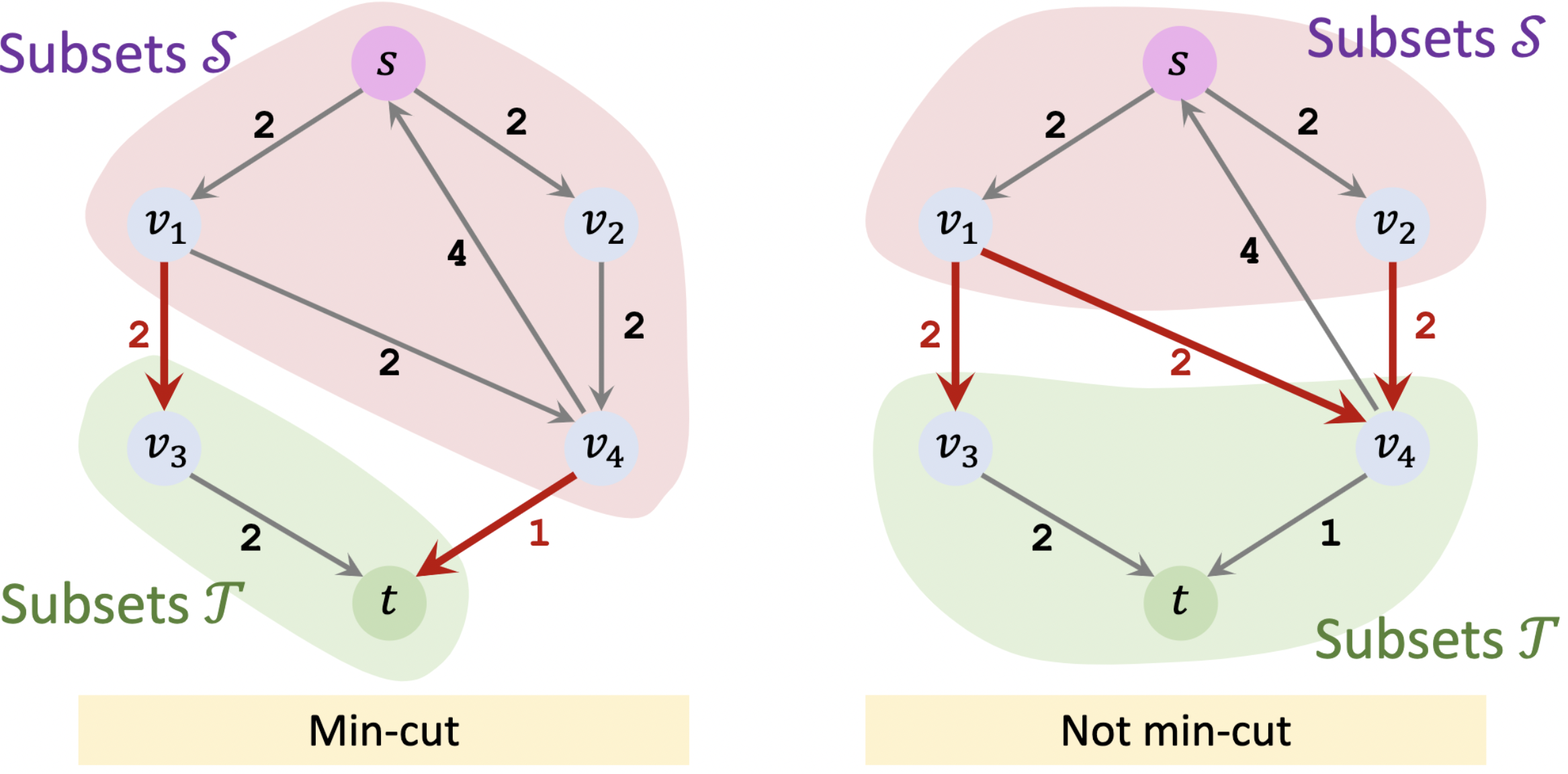
如上图所示,我们去除图中红色的边,使得不存在任意一套路径可以从起点 s s s t t t 。去除这些边后,定点集 V V V S u b s e t S _{Subset}S S u b s e t S S u b s e t T _{Subset}T S u b s e t T 然而这样的集合划分并不唯一 。
【注意⚠️】图中有一条边 v 4 ⟶ 4 s v_4 \stackrel{4}\longrightarrow s v 4 ⟶ 4 s S u b s e t S _{Subset}S S u b s e t S S u b s e t T _{Subset}T S u b s e t T 不存在任意一套路径可以从起点 s s s t t t 。所以我们不用去管他。
容量 C a p a c i t y ( S , T ) Capacity(S,T) C a p a c i t y ( S , T ) S u b s e t S _{Subset}S S u b s e t S S u b s e t T _{Subset}T S u b s e t T 边的权重之和 ,
上图中左边的容量 C a p a c i t y 左 ( S , T ) = 2 + 1 = 3 Capacity_左(S,T) = 2+1 =3 C a p a c i t y 左 ( S , T ) = 2 + 1 = 3
右边的“S-T Cut”容量 C a p a c i t y 右 ( S , T ) = 2 + 2 + 2 = 6 Capacity_右(S,T) = 2+2+2 = 6 C a p a c i t y 右 ( S , T ) = 2 + 2 + 2 = 6
【最小割】:Minimum S-T Cut (Min-Cut),是在所有“S-T Cut” 中容量最小的那个。目标是用最小的“力气”(权)就可以截断水流(起点 s s s t t t
对于一个网络流问题,最大流的流量 就等于 最小割的容量 ,即
M a x f l o w = M i n c u t Max \;flow = Min\;cut
M a x f l o w = M i n c u t
我们可以将 寻找最小割的问题 等价转化为 寻找最大流问题 :
在 寻找最大流问题 中,在最后一次迭代中去除回溯路径 的残差图 (Residual Graph) 中,从起点 s s s S u b s e t S _{Subset}S S u b s e t S S u b s e t T _{Subset}T S u b s e t T ( S , T ) (S,T) ( S , T )